【July】【Machine Leraning】1.微积分和概率论
1. 两边夹定理
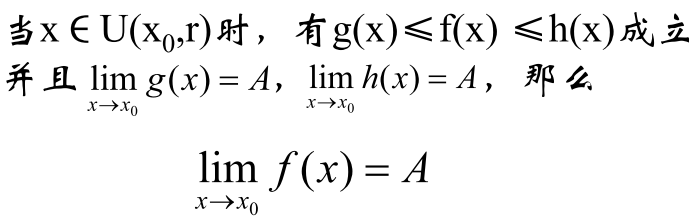
- 形象化解释
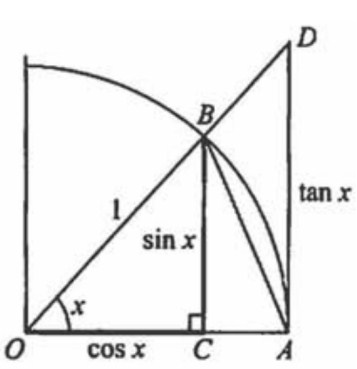
- 单位圆,半径 = 1
- BC线段( sin x) < AB线段 < AB弧( x) <AD线段
- 可以得到
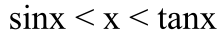
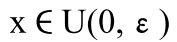
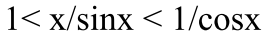
- 求极限

- 得到
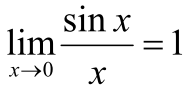
- 例子,求解
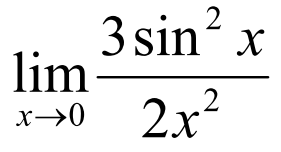 = 3/2
= 3/2
2. 极限存在定理
- 数列如果单调递增且有上界,则一定有极限。
- 二项式展开定理

- 考察一个数列

- 由此可见,这个数列是个递增数列 且 小于3
- 可以推断,这个数列的极限也应当小于3,大于2,用符号e作为记号
- 如果n取实数,而不是整数.
- 构造不等式

- 左侧和右侧分别求极限
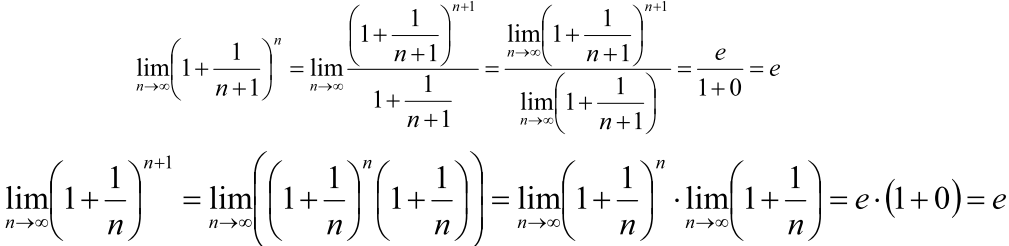
- 根据两边夹定理,可以得到

- 构造不等式
3. 导数
- 一阶导数:曲线的斜率 => 曲线变化快慢
- 二阶导数:斜率的变化快慢 => 曲线的凸凹性
- 物理:加速度是二阶导数,且导数方向在曲线凹的一侧
- 常用导数的求解
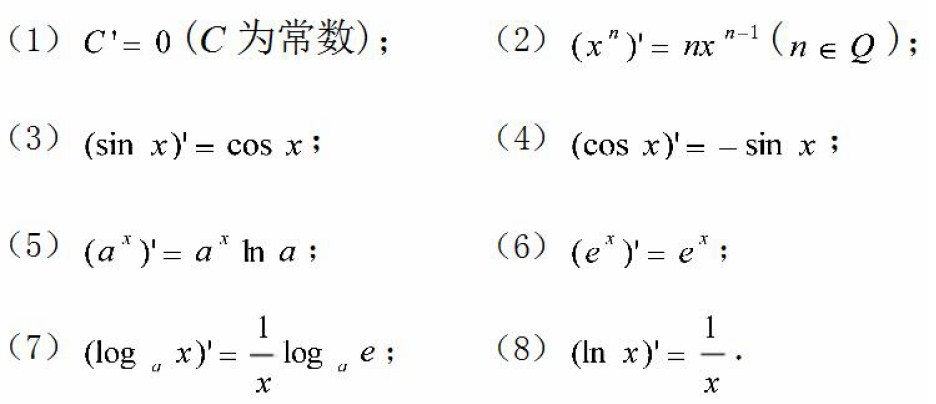
- 应用,求解函数的最小值
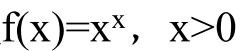
- 核心是利用两侧取对数和导数 = 0的策略来求解

- 核心是利用两侧取对数和导数 = 0的策略来求解
4. Taylor 和 Maclaurin 公式
- Taylor基本公式
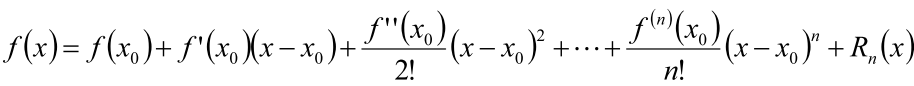
- 在点展开
- 展开到项,加上高阶无穷小
- 如果要求在处展开,则得到Maclaurin公式
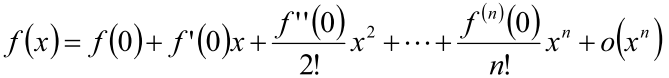
- 对复杂函数,求解函数在原点展开

- 如果一个函数求解有困难,通过展开可以得到多项式加权的和
- 实际过程中需要改进
- 整数+小数来表达一个实数
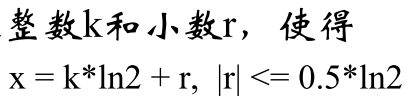
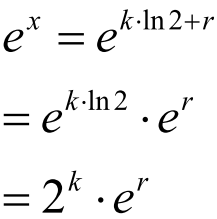
- 第一项可以计算,第二项一定是收敛的
- 整数+小数来表达一个实数
- 应用,分析熵的函数
- 将在一阶展开,可以得到
- 则熵函数可以写为
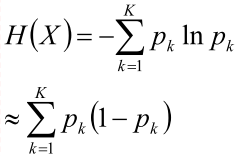
5. 方向导数
函数f(x)在任意方向L的导数,φ是L与x轴方向夹角
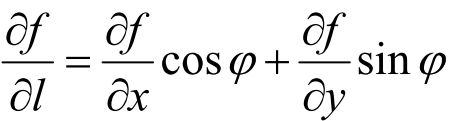
梯度grad f(x),高程变化最快的方向,抛去cos,sin函数
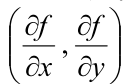
6. 凸函数
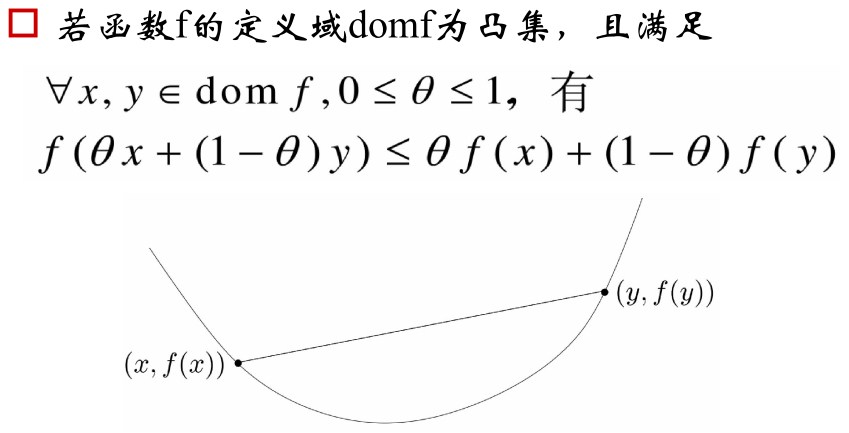
形象化解释
- 不等式左侧,是曲线上一点
- 不等式右侧,是直线上一点
- 直线上一点 > 曲线上一点
- 割线在上,函数在下 => 凸函数
判定方法

- 拓展更多维度,得到不等式

- 例子,完成证明
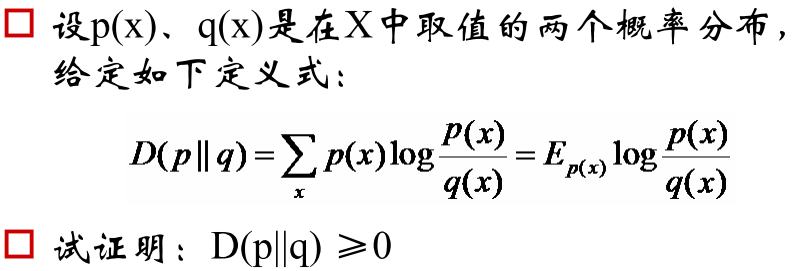


7. 概率论
7.1 概率的基本定义

- 事件一定发生 => P(X) = 1,反之不一定成立
- 事件一定不发生 => P(X) = 0,反之不一定成立
- 即概率 = 0,不意味着不可能发生
- 离散 => 概率
- 连续变量 => 概率密度
7.2 累积分布函数

- 给出f(x),值域是[0,1] => 累计概率 => 求导,得到概率密度(Logistic回归)
- CDF: Cumulative Distribution Function,累计分布函数
- PDF: Probability Density Function,概率密度函数
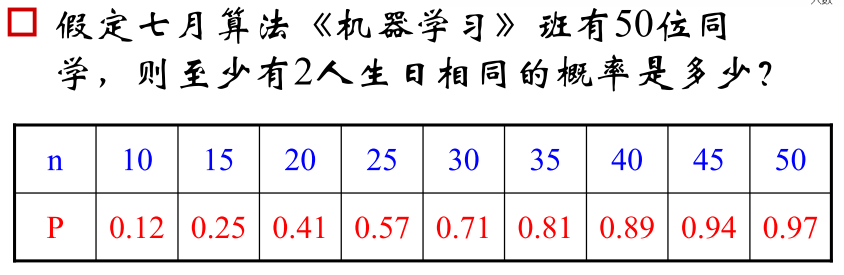
7.3 例子:古典概型基本思路
- 例子

- 算所有概型个数

- 算有效事件个数

- 两者相除即可得到结论
- 算所有概型个数
- 转化为另外一个例题,生日悖论
7.4 组合数 - 装箱问题
- 例子

- 全部事件
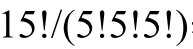
- 有效事件
3! 次品摆放
 正品摆放
正品摆放
- 全部事件
- 组合数关系

- n:物品总数
- k:组的类别
- n_k: 每组个数
- 进一步,如果明确 n = 2

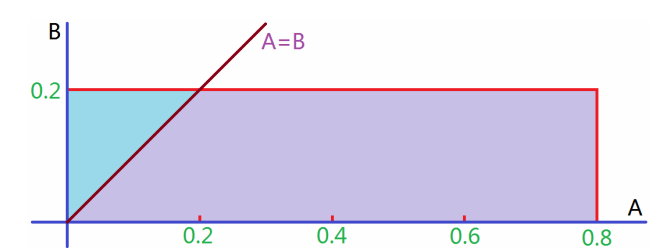
7.5 商品推荐 - 几何概型

- A商品匹配度0.8,B商品匹配度0.2
- 系统随机为A生成在[0, 0.8]的均匀分布
- 系统随机为B生成在[0, 0.2]的均匀分布
- 系统全局为0.8*0.2的一个矩形,画一条A=B的直线,进行切割

7.6 概率公式总结

7.7 Bayes公式的应用

- 是否校准

- 校准和中靶结合
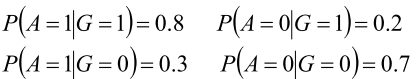
- 校准|中靶
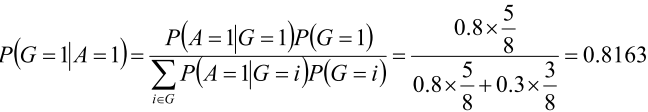
7.8 两个学派
- 给定系统样本 => 求解系统该参数
- 矩估计
- MLE,MaxEnt, EM
- 频率学派
- 贝叶斯模型
- 参数本身变化,服从某个分布
- 在分布约束下 => 目标函数极大极小
7.9 Bayes公式分析

- 先验概率:没有任何其他信息支撑
- 后验概率:已知数据的情况下
- 似然函数:给定概率分布 + 参数,求时间发生的概率
7.10 分布
Possion分布
将e^x的展开式处理
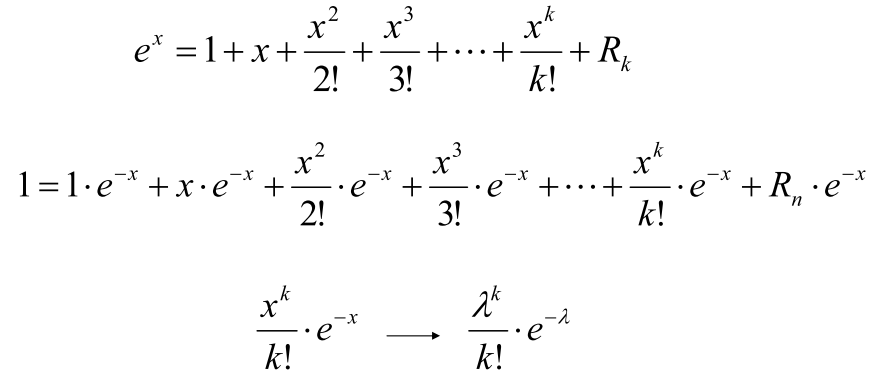
- 处理汽车站候车人数,自然灾害发生
- 即事件以平均瞬时速率λ随机独立出现,则在单位时间出现的次数 => Possion分布
指数分布
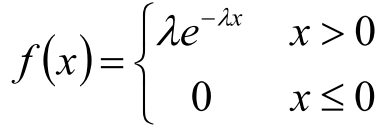
- 无记忆效应

- 无记忆效应
总结
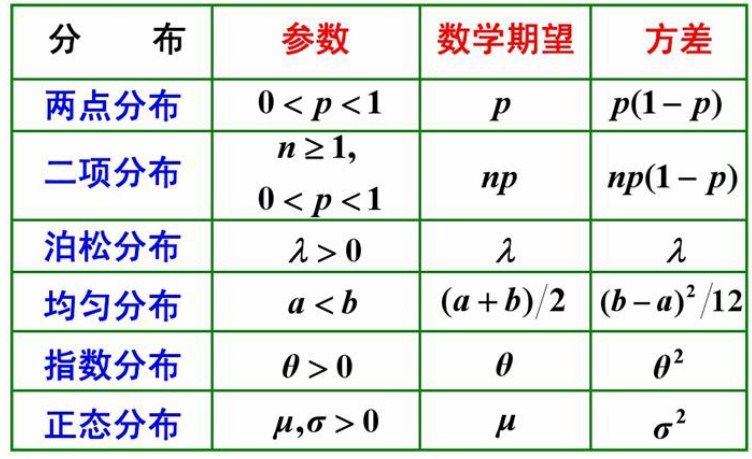
用指数族 - exponential family来表达
- Logistic - Sigmond 函数


- 函数递增
- 值域[0, 1]
- 神经网络的激活函数
求导数
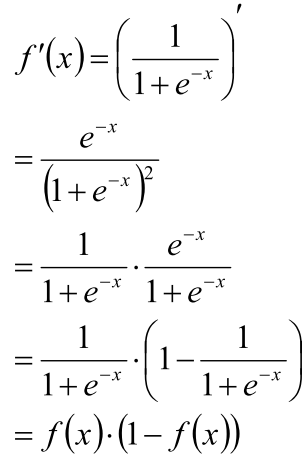
Gamma函数

- Gamma函数是阶乘的推广
e-mail: kongww.nudt [AT] gmail.com
WeChat/QQ: 40804097



