c语言刷leetcode——图（邻接表、邻接矩阵）

目录

0.图和树的关系

  1. 树是特殊的图，且是有向图
  2. 树中没有环，而图中可能有

1.图的存储方式

  • 图由点集和边集组成
  • 图分为有向图和无向图，无向图可以理解为双向有向图

1.1 邻接表 和 邻接矩阵

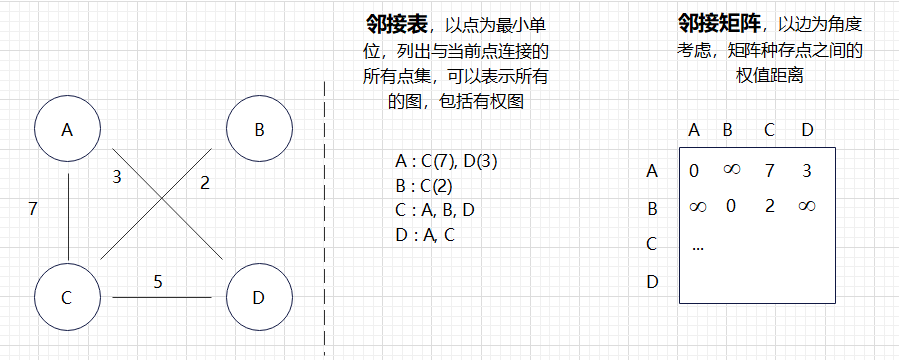
  • 常见的图存储方式由邻接表（点集为核心）和邻接矩阵（边集为核心）
    邻接表：可以直接查出后续有多少邻接点
    邻接矩阵： 可以直接查出每条边
    image

1.1.1 邻接表代码实现——leetcode 1971. 寻找图中是否存在路径

视频参考
- 代码如下，参考结构体和构建邻接表的方法：

typedef struct Node {
    int val;
    struct Node *next;
} Node;

// Node adj[MAX]; // 邻接表：存每个索引位置对应的头节点
/*
头节点 -> 接后面链接的其他节点
[0]-> [val | ] -> [val | ] -> ... -> NULL
[1]-> [val | ] -> [val | ] -> ... -> NULL
[2]-> [val | ] -> [val | ] -> ... -> NULL
...
*/

Node *New(int val, Node *connect)
{
    Node *new = malloc(sizeof(Node));
    new->val = val;
    new->next = connect;

    return new;
}

bool validPath(int n, int** edges, int edgesSize, int* edgesColSize, int source, int destination)
{
    Node *adj[n];
    int i;
    // 初始化
    for (i = 0; i < n; i++) {
        adj[i] = NULL;
    }
    // 建图
    for (i = 0; i < edgesSize; i++) {
        adj[edges[i][0]] = New(edges[i][1], adj[edges[i][0]]);
        adj[edges[i][1]] = New(edges[i][0], adj[edges[i][1]]);
    }

    // bfs
    int used[n]; // 去重
    memset(used, 0, sizeof(int) * n);
    int head = 0, tail = 0;
    int queue[n];
    queue[tail++] = source;
    used[source] = 1; // 访问过了
    Node *cur = NULL;
    while (head != tail) {
        int val = queue[head++];
        if (val == destination) {
            return true; // 找到了
        }
        cur = adj[val];
        while (cur != NULL) {
            if (used[cur->val] == 0) {
                queue[tail++] = cur->val; // 入队
                used[cur->val] = 1; // 访问过了
            }
            cur = cur->next;
        }
    }

    return false;
}

1.2 代码实现一种全能的图模板

  • TODO

2. 图的遍历方式

2.1 宽度优先遍历

  • 队列实现，hash去重

2.2 深度优先遍历

  • 栈实现，hash去重

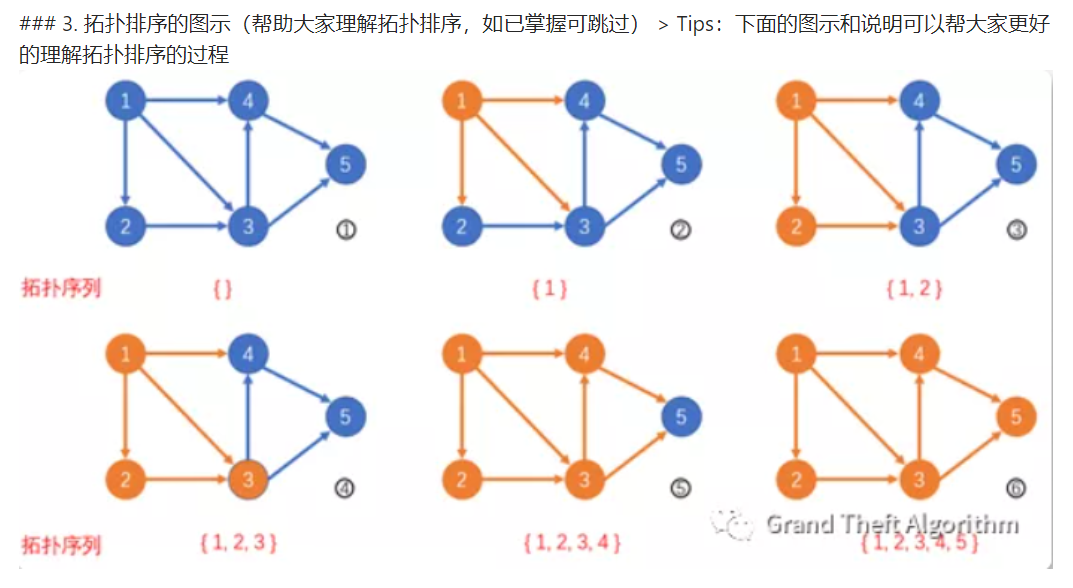
3. 拓扑排序

3.1 拓扑排序的常见使用场景

  1. 编译时的编译顺序，每个包之间的相互依赖关系，比如B依赖A，想要编译B，则需要先编译A
  2. 生活中需要先穿内衣，再穿衬衣，最后穿裤子和外套，也是一种拓扑排序的思想

3.2 题目

802. 找到最终的安全状态
841. 钥匙和房间
133. 克隆图
997. 找到小镇的法官

  • 不同太死板，简单问题两个数组统计入度和出度即可

4. 生成最小生成树的两个算法，要求无向图，类似并查集的优化

  • 最小生成树——删除冗余连接的边，并且保证权值累加和最小

4.1 k算法——kruskal算法——避圈法——需要借助的数据结构：并查集

  • 并查集

4.2 p算法——prim算法——破圈法——需要借助的数据结构：堆

5. 迪杰斯特拉算法——最短路径问题

  • 有向无负边图

5.1 模板题

743.网络延迟时间

  • 算法思想 ：从起点开始到其他节点，每次走的时候，观察能否使得目前存的记录更小，有则更新，参考下面的题目

5.1.1 代码

#define INF 100000

void InitArr(int *arr, int len, int aim)
{
    for (int i = 0; i < len; i++) {
        arr[i] = aim;
    }
}

int GetMinAndUnUsedNode(int *dist, int *used, int n)
{
    int min = -1;
    for (int i = 0; i < n; i++) {
        if (used[i] == 0) {
            continue;
        }
        if (min == -1 || dist[i] < dist[min]) {
            min = i;
        }
    }
    return min;
}

int networkDelayTime(int** times, int timesSize, int* timesColSize, int n, int k)
{
    int res = -1;
    int i, j;
    // 1.用邻接矩阵存边集信息
    int graph[n][n];
    for (i = 0; i < n; i++) {
        for (j = 0; j < n; j++) {
            graph[i][j] = INF;
        }
    }
    for (i = 0; i < timesSize; i++) {
        int from = times[i][0];
        int to = times[i][1];
        int weight = times[i][2];
        graph[from-1][to-1] = weight;
    }

    // 2.准备距离数组 : ans为dist中原点到其他点的最大值
    int dist[n];
    InitArr(dist, n, INF); // 原点head到q其他点的距离为INF
    dist[k - 1] = 0; // 原点head到自己的距离为0

    // 3.准备hash表防止重复
    int used[n]; // -1: 没用过， 0: 用过
    InitArr(used, n, -1);

    // 4.每次在dist中取距离最短且没用过的点，作为起点
    for (i = 0; i < n; i++) {
        int cur = GetMinAndUnUsedNode(dist, used, n);
        used[cur] = 0;

        // 更新结果，如果某个点从原点无法到达，最终结果都是INF
        res = fmax(res, dist[cur]);
        for (j = 0; j < n; j++) {
            dist[j] = fmin(dist[j], dist[cur] + graph[cur][j]);
        }
    }

    return res == INF ? -1 : res;
}

5.1.2 参考

参考

posted @ 2023-07-07 16:47  胖白白  阅读(35)  评论(0)  编辑  收藏  举报