笔记1. O(NlogN)的排序算法

目录

• 准备工作
• 递归行为——求数组的最大值
• master公式
• 归并排序——912. 排序数组
  • Merge函数
  • 归并排序主函数
  • nlogn与n^2排序本质差距
  • 小和问题
  • 剑指 Offer 51. 数组中的逆序对
• 快排
  • 荷兰国旗问题
  • 快排 1.0
  • 快排 2.0
  • 快排 3.0

准备工作

• 打印数组

void PrintfNums(int *nums, int numsSize)
{
    for (int i = 0; i < numsSize; i++) {
        printf("%d ", nums[i]);
    }
    printf("\n");
}

• 交换元素

void Swap(int *a, int *b)
{
    int tmp = *a;
    *a = *b;
    *b = tmp;
}

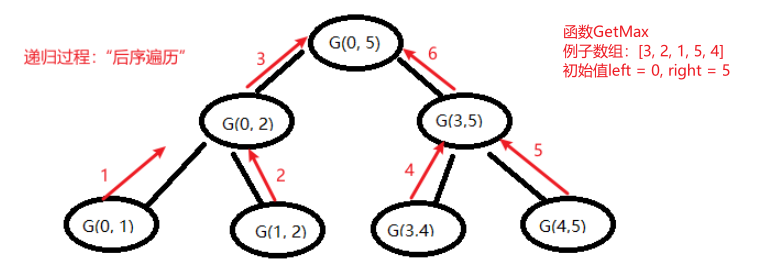
递归行为——求数组的最大值

int GetMax(int *nums, int left, int right)
{
    if (left >= right) return nums[left];

    int mid = left + ((right - left) >> 1);
    int leftMax = GetMax(nums, left, mid);
    int rightMax = GetMax(nums, mid + 1, right);
    return fmax(leftMax, rightMax);
}

master公式

归并排序——912. 排序数组

Merge函数

void Merge(int leftNums[], int leftSize, int rightNums[], int rightSize, int *resNums, int resSize)
{
    int leftId = 0, rightId = 0;
    int resId = 0;
    while (leftId < leftSize && rightId < rightSize) {
        if (leftNums[leftId] < rightNums[rightId]) {
            resNums[resId] = leftNums[leftId++];
            printf("left = %d\n", resNums[resId]);
        } else {
            resNums[resId] = rightNums[rightId++];
            printf("right = %d\n", resNums[resId]);
        }
        resId++;
    }

    if (leftId < leftSize) {
        memcpy(&resNums[resId], &leftNums[leftId], sizeof(int) * (leftSize - leftId));
    }

    if (rightId < rightSize) {
        memcpy(&resNums[resId], &rightNums[rightId], sizeof(int) * (rightSize - rightId));
    }
}

void Merge(int nums[], int left, int mid, int right)
{
    int *help = malloc(sizeof(int) * (right - left + 1));
    int leftId = left, rightId = mid + 1;
    int id = 0;
    while (leftId <= mid && rightId <= right) {
        if (nums[leftId] <= nums[rightId]) {
            help[id] = nums[leftId++];
        } else {
            help[id] = nums[rightId++];
        }
        id++;
    }
    // if (leftId <= mid) {
    //     help[id++] = nums[leftId++];
    // }
    memcpy(&help[id], &nums[leftId], sizeof(int) * (mid - leftId + 1));

    // if (rightId < right) {
    //     help[id++] = nums[rightId++];
    // }
    memcpy(&help[id], &nums[rightId], sizeof(int) * (right - rightId + 1));

    // for (id = 0; id < right - left + 1; id++) {
    //     nums[left + id] = help[id];
    // }
    memcpy(&nums[left], &help[0], sizeof(int) * (right - left + 1));
    free(help);
}

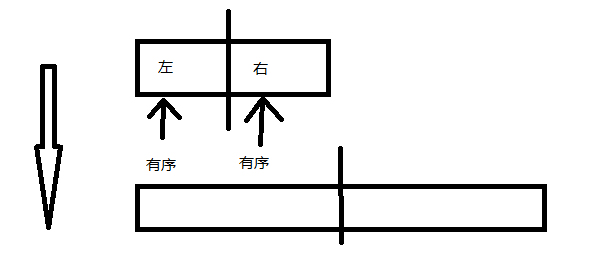
归并排序主函数

void Process(int nums[], int left, int right)
{
    if (left >= right) {
        return;
    }

    int mid = left + ((right - left) >> 1);
    Process(nums, left, mid);
    Process(nums, mid + 1, right);
    Merge(nums, left, mid, right);
}

nlogn与n^2排序本质差距

n^2比如冒泡排序，第一次比较n次才搞定一个数，第二次比较n-1次才搞定第二个数，以此类推，浪费了大量的比较行为
nlogn则不会，比如归并排序，每次解决整体的部分，然后再拿其中有序的部分再去比较，解决更大的整体，在这个过程中，每次的比较行为没有被浪费

小和问题

• 数组中，求每个元素的小和之和，小和的概念：每个数小于右边数的总和

---

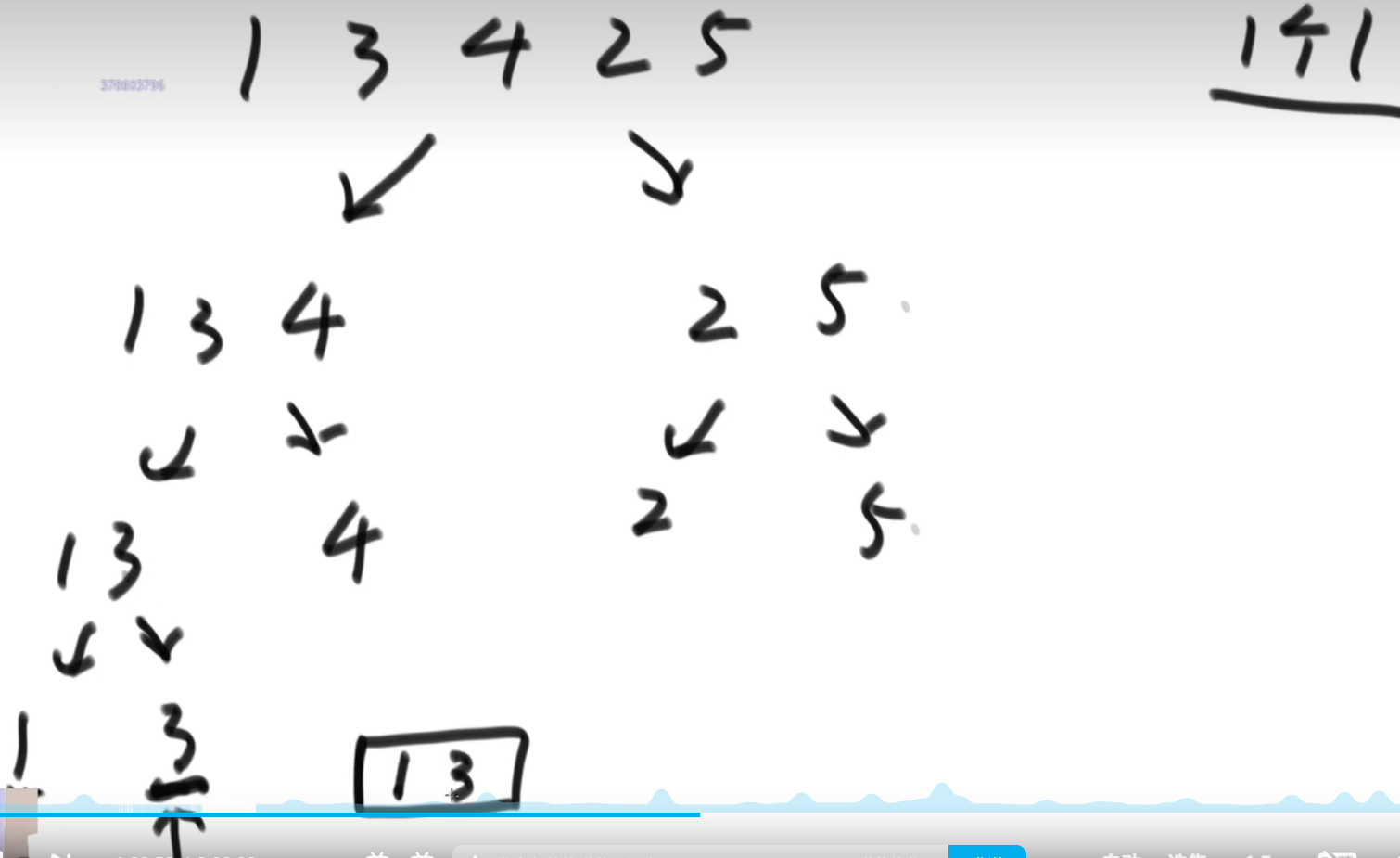
1. 必须要一边排序一边计算小和，左组和右组计算小和的数量通过下标的方式
2. 和归并排序中的merge有一点点不同，就是当左组和右组遇到相等的数时，一定要先拷贝右组的数（为了小和计算准确）
   
   

int MergeXiaohe(int nums[], int left, int mid, int right)
{
    int res = 0;
    int *help = malloc(sizeof(int) * (right - left + 1));
    int leftId = left, rightId = mid + 1;
    int id = 0;
    while (leftId <= mid && rightId <= right) {
        if (nums[leftId] < nums[rightId]) { // 注意这里判断条件不能加等号，因为小和必须满足右边的比左边的大
            res += (nums[leftId] * (right - rightId + 1)); // 小和累加
            help[id] = nums[leftId++];
        } else {
            help[id] = nums[rightId++];
        }
        id++;
    }

    memcpy(&help[id], &nums[leftId], sizeof(int) * (mid - leftId + 1));
    memcpy(&help[id], &nums[rightId], sizeof(int) * (right - rightId + 1));
    memcpy(&nums[left], &help[0], sizeof(int) * (right - left + 1));
    free(help);

    return res;
}

/* 小和问题 */
int ProcessXiaoHe(int nums[], int left, int right)
{
    if (left >= right) {
        return 0 ;
    }

    int mid = left + ((right - left) >> 1);
    /*
    先求左组并排好序
    再求右组并排好序
    然后再归并
    */
    return ProcessXiaoHe(nums, left, mid) + 
           ProcessXiaoHe(nums, mid + 1, right) + 
           MergeXiaohe(nums, left, mid, right);
}

剑指 Offer 51. 数组中的逆序对

int Cnt(int *nums, int left, int mid, int right)
{
    int res = 0;
    int id = 0;
    int *help = malloc(sizeof(int) * (right - left + 1));
    int leftId = left;
    int rightId = mid + 1;

    while (leftId <= mid && rightId <= right) {
        if (nums[leftId] > nums[rightId]) {
            // res += (right - rightId + 1); // 计算逆序对结果：这样是不对的
            res += (mid - leftId + 1); // 计算逆序对结果：这样是对的
            // 7 5 6 4 2 1 3
            help[id] = nums[rightId++];
        } else {
            help[id] = nums[leftId++];
        }
        id++;
    }

    for (; leftId <= mid; leftId++) {
        help[id++] = nums[leftId];
        // res += (rightId - (mid + 1));
    }
    for (; rightId <= right; rightId++) {
        help[id++] = nums[rightId];
    }
    
    for (int k = 0; k <= (right - left); k++) {
        nums[k + left] = help[k];
    }
    free(help);
    return res;
}

int Pro(int *nums, int left, int right)
{
    if (left >= right) {
        return 0;
    }

    int mid = left + ((right - left) >> 1);
    return Pro(nums, left, mid) + Pro(nums, mid + 1, right) + Cnt(nums, left, mid, right);
}

int reversePairs(int* nums, int numsSize)
{
    return Pro(nums, 0, numsSize - 1);
}

快排

荷兰国旗问题

1. 问题1：给你一个数target，在数组中将小于等于target的数都放到左边，大于等于target的数都放右边，要求空间复杂度0（1），时间复杂度0（N）

2. 问题1：给你一个数target，在数组中将小于target的数都放到左边，等于target的数放中间，大于等于target的数都放右边，要求空间复杂度0（1），时间复杂度0（N）

/*
荷兰国旗问题: 小于等于区域，推着大于区域往后走
1. 准备变量boundary，作为小于等于的右边界，初始值为0，然后可能会依次递增到0 1 2
2. 准备变量i，遍历整个数组

升级：
[ < ][ = ][ > ]
1. [i] < target, [i] 和 < 区的下一个做交换，< 区右扩，i++;
2. [i] == target, i++;
3. [i] > target, [i] 和 > 区的前一个做交换，> 区坐扩，i不变
*/
void LeftToRight(int *nums, int numsSize, int target)
{
    int boundary = -1;
    for (int i = 0; i < numsSize; i++) {
        if (nums[i] <= target) {
            Swap(&nums[i], &nums[boundary + 1]);
            boundary++;
        }
    }
}

void LeftEqualRight(int *nums, int numsSize, int target)
{
    int leftBoundary = -1;
    int rightBoundary = numsSize;
    int i = 0;
    int tmp = 0;
    while (i < numsSize) {
        if (leftBoundary + tmp >= rightBoundary - 1) {
            break;
        }
        if (nums[i] < target) {
            Swap(&nums[i], &nums[leftBoundary + 1]);
            leftBoundary++;
            i++;
        } else if (nums[i] == target) {
            i++;
            tmp++;
        } else {
            Swap(&nums[i], &nums[rightBoundary - 1]);
            rightBoundary--;
        }
    }
}

快排 1.0

荷兰国旗基础解法

快排 2.0

荷兰国旗进阶解法
1.0和2.0最差时间复杂度都是0(N^2)，对于本身就是有序的数组

快排 3.0

划分值的选择需要有随机性，这样好情况和坏情况是概率事件

void SwapNums(int *nums, int l, int r)
{
    int tmp = nums[l];
    nums[l] = nums[r];
    nums[r] = tmp;
}

int g_pos[2] = {-1, -1};
/*
* 增加返回值记录左右边界
* 比较值默认取数组的最后一个
*/
void Partition(int *nums, int left, int right)
{
    // 每次选择数组中的最后一个数交换后作为分界点
    int target = nums[right];

    int less = left - 1; // < 区右边界
    int more = right + 1; // > 区左边界

    while (left < more) {
        if (nums[left] < target) {
            SwapNums(nums, left, less + 1);
            left++;
            less++;
        } else if (nums[left] == target) {
            left++;
        } else {
            SwapNums(nums, left, more - 1);
            more--;
        }
    }
    g_pos[0] = less;
    g_pos[1] = more;
}

void QuickSort(int *nums, int left, int right)
{
    if (left < right) {
        // 每次选择数组中的随机数，与最后一个数交换后作为分界点
        int randId = rand() % (right - left + 1) + left;
        SwapNums(nums, right, randId);

        Partition(nums, left, right);
        QuickSort(nums, left, g_pos[0]);
        QuickSort(nums, g_pos[1], right);
    }
}

int* sortArray(int* nums, int numsSize, int* returnSize)
{   
    QuickSort(nums, 0, numsSize - 1);

    *returnSize = numsSize;
    return nums;
}