c语言刷leetcode——常见数据结构实现
目录
全文参考链接
- 1.leetcode
- 2.数据结构与算法之美
0.数组
参考链接
低效的“插入”和“删除”
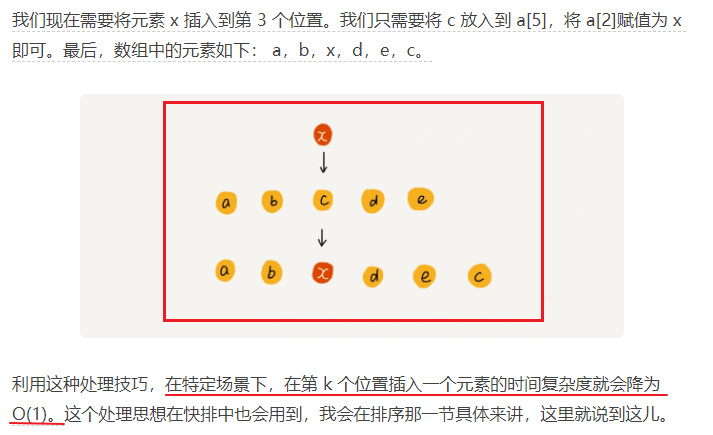
警惕数组的访问越界问题
int main(int argc, char* argv[]){
int i = 0;
int arr[3] = {0};
for(; i<=3; i++){
arr[i] = 0;
printf("hello world\n");
}
return 0;
}
- 运行结果：可能会无限打印，也可能不会；如果会的话，要考虑unix中栈的扩展方向，以及栈由高地址向低地址生长：
函数体内的局部变量存在栈上，且是连续压栈。在Linux进程的内存布局中，栈区在高地址空间，从高向低增长。变量i和arr在相邻地址，且i比arr的地址大，所以arr越界正好访问到i。当然，前提是i和arr元素同类型，否则那段代码仍是未决行为。
支持动态扩容
1.链表
单链表
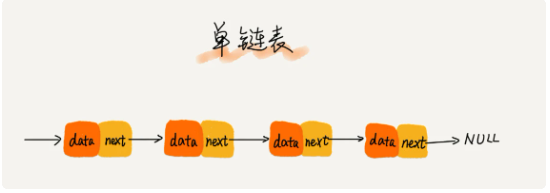
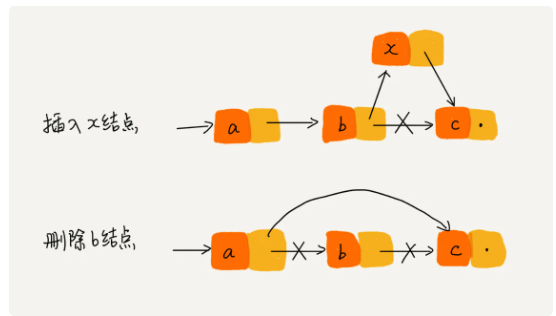
双向链表
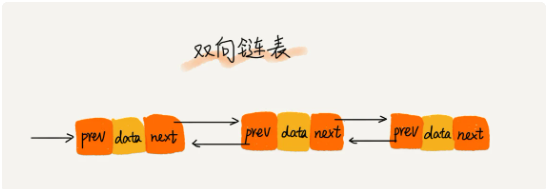
单链表与双链表的删除操作
- 删除操作的两种情况：
- 删除结点中“值等于某个给定值”的结点；这种情况用单链表还是双链表没啥区别
- 删除给定指针指向的结点；这种情况指的是已经直到了要删除的结点地址，但是要从链表中删除需要知道其前节点与后结点，因此用双链表效率更高
(非常详细的画图和实现)如何基于链表实现 LRU 缓存淘汰算法？146. LRU 缓存
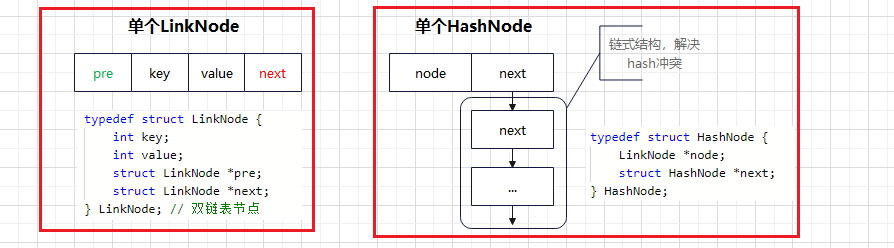
typedef struct LinkNode {
int key;
int value;
struct LinkNode *pre;
struct LinkNode *next;
} LinkNode;
typedef struct HashNode {
LinkNode *node;
struct HashNode *next; // head->next->next这种链式结构，解决hash冲突，注意第一个next不为空且就是head
} HashNode;
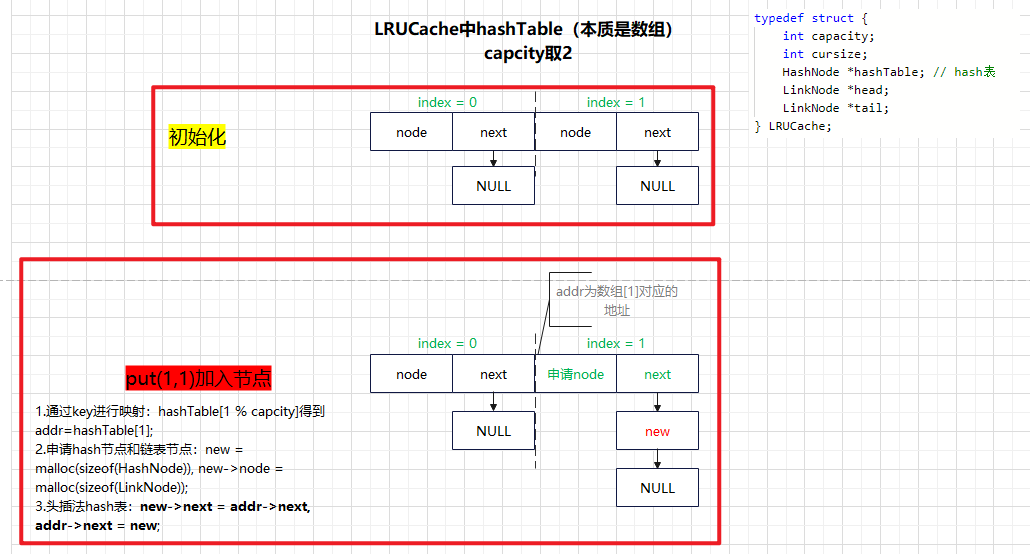
typedef struct {
int capacity;
int cursize;
HashNode *hashTable;
LinkNode *head;
LinkNode *tail;
} LRUCache;
LinkNode* LinkNodeCreate(int key, int value)
{
LinkNode *node = malloc(sizeof(LinkNode));
node->key = key;
node->value = value;
node->pre = NULL;
node->next = NULL;
return node;
}
LRUCache* lRUCacheCreate(int capacity)
{
LRUCache *obj = malloc(sizeof(LRUCache));
obj->capacity = capacity;
obj->cursize = 0;
// 初始hash表，并清空, calloc
obj->hashTable = calloc(capacity, sizeof(HashNode));
// 双链表(前后两个虚拟节点)
obj->head = LinkNodeCreate(0, 0);
obj->tail = LinkNodeCreate(0, 0);
obj->head->next = obj->tail;
obj->tail->pre = obj->head;
return obj;
}
/* 根据key从hashTable中得到node */
HashNode* HashMap(HashNode *hashTable, int key, int capacity)
{
return &hashTable[key % capacity];
}
void HeadInsert(LinkNode* head, LinkNode *node)
{
// 如果node不在链表中，则直接加入头部
if (node->pre == NULL && node->next == NULL) {
node->next = head->next;
node->pre = head;
head->next->pre = node;
head->next = node;
} else { // 否则进行更新：先删后加
LinkNode *first = head->next; // 链表的第一个数据节点
if (first != node) { // 如果已经在头部则不处理
// 先删
node->pre->next = node->next;
node->next->pre = node->pre;
// 再加
node->next = first;
node->pre = head;
head->next = node;
first->pre = node;
}
}
}
/* 函数功能复用：用来判断key是否在hashTable中 */
int lRUCacheGet(LRUCache* obj, int key)
{
HashNode* addr = HashMap(obj->hashTable, key, obj->capacity);
addr = addr->next;
if (addr == NULL) {
// 说明hashTable对应的hash节点为空，一个节点还没添加
return -1;
}
// 去找key对应的节点
while (addr->next != NULL && addr->node->key != key) {
addr = addr->next;
}
// 找到了
if (addr->node->key == key) {
// 更新节点在链表中的位置到头部(最新位置)
HeadInsert(obj->head, addr->node);
return addr->node->value;
}
return -1;
}
void lRUCachePut(LRUCache* obj, int key, int value)
{
HashNode* addr = HashMap(obj->hashTable, key, obj->capacity);
// case1. key不存在
if (lRUCacheGet(obj, key) == -1) {
// case1.1 已经满了
if (obj->cursize == obj->capacity) {
HashNode *new = malloc(sizeof(HashNode));
new->node = LinkNodeCreate(key, value);
LinkNode *last = obj->tail->pre;
// a.hash中找到对应的节点删除，再添加新的映射关系
HashNode *addrdel = HashMap(obj->hashTable, last->key, obj->capacity);
HashNode *ptr = addrdel;
addrdel = addrdel->next;
while (addrdel->node->key != last->key) {
ptr = addrdel;
addrdel = addrdel->next;
}
ptr->next = addrdel->next; // 在 &hashTable[key % capacity] 中删除节点
addrdel->next = NULL;
addrdel->node = NULL; // 解除映射
free(addrdel); // 回收资源
// 头插法：连接到 &hashTable[key % capacity] 中
new->next = addr->next, addr->next = new;
// b.方法1：链表中last节点删除，然后将new节点添加到头部；方法2(这里采用)：最大化利用双链表中的结点，对其重映射(节约空间)
new->node = last; // 最大化利用双链表中的结点，对其重映射(节约空间)
last->key = key; // 重新赋值
last->value = value;
HeadInsert(obj->head, last); // 更新最近使用的数据
} else { // case1.2 还没满
HashNode *new = malloc(sizeof(HashNode));
new->node = LinkNodeCreate(key, value);
// 头插法：连接到 &hashTable[key % capacity] 中
new->next = addr->next, addr->next = new;
HeadInsert(obj->head, new->node);
++(obj->cursize);
}
} else { // case2. key已存在
obj->head->next->value = value; // lRUCacheGet已经更新了链表表头，这里不用再更新
}
}
void lRUCacheFree(LRUCache* obj)
{
LinkNode *node = obj->head;
while (node != NULL) {
LinkNode *tmp = node;
node = node->next;
free(tmp);
}
free(obj->hashTable);
free(obj);
}
/**
* Your LRUCache struct will be instantiated and called as such:
* LRUCache* obj = lRUCacheCreate(capacity);
* int param_1 = lRUCacheGet(obj, key);
* lRUCachePut(obj, key, value);
* lRUCacheFree(obj);
*/
148. 排序链表
141. 环形链表
707. 设计链表
114. 二叉树展开为链表
2.栈
单调栈
入门题
给一个数组，返回一个大小相同的数组。返回的数组的第i个位置的值应当是，对于原数组中的第i个元素，至少往右走多少步，才能遇到一个比自己大的元素（如果之后没有比自己大的元素，或者已经是最后一个元素，则在返回数组的对应位置放上-1）
-
正序遍历数组
-
逆序遍历数组
/*
给一个数组，返回一个大小相同的数组。返回的数组的第i个位置的值应当是，对于原数组中的第i个元素，至少往右走多少步，才能遇到一个比自己大的元素（如果之后没有比自己大的元素，或者已经是最后一个元素，则在返回数组的对应位置放上-1）
*/
void PrintfNums(int *nums, int numSize)
{
for (int i = 0; i < numSize; i++) {
printf("%d ", nums[i]);
}
printf("\n");
}
int* largestRectangleArea(int* nums, int numSize)
{
// nums : [2, 1, 5, 6, 2, 3]
int top = 0;
int stack[numSize];
int i;
int *res = malloc(sizeof(int) * numSize);
for (i = numSize - 1; i >= 0; i--) {
while (top != 0 && nums[stack[top - 1]] <= nums[i]) {
top--;
}
res[i] = (top == 0) ? -1 : (stack[top - 1] - i);
stack[top++] = i;
}
PrintfNums(res, numSize); // res : [2 1 1 -1 1 -1 ]
return res;
}
496. 下一个更大元素 I
最后在栈中存放的，就是一个单调的数组。 比如215623，最后栈中就是123
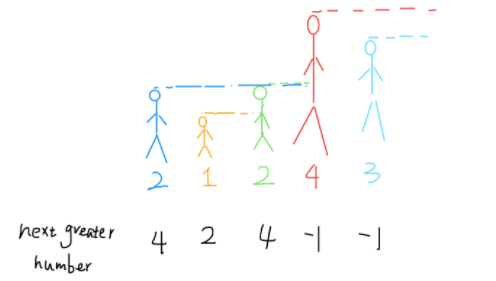
503. 下一个更大元素 II
- 单调栈存的是数组下标
- 处理循环数组的思路：
- 拷贝1份数组到原数组某，即数组长度 x 2；
这里用这种方法更方便 - 当成循环队列做，每次对下标进行取余i % len;
题号：20, 155, 232, 844, 224, 682, 496
20. 有效的括号
150. 逆波兰表达式求值
3.队列
622. 设计循环队列
641. 设计循环双端队列
1670. 设计前中后队列
4.递归
递归需要满足的三个条件
- 自己总结：
1.函数参数明确；2.函数内逻辑明确；3.递归终止条件明确
- 一个问题的解可以分解为几个子问题的解
- 这个问题与分解之后的子问题，除了数据规模不同，求解思路完全一样
- 存在递归终止条件
如何编写递归代码？
- 写出递推公式，找到终止条件
递归需要注意的问题：1.防止堆栈溢出 2.避免重复计算
- 防止堆栈溢出
// 全局变量，表示递归的深度。
int depth = 0;
int f(int n) {
++depth；
if (depth > 1000) throw exception;
if (n == 1) return 1;
return f(n-1) + 1;
}
- 避免重复计算：用hash记录计算过的结果
public int f(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
// hasSolvedList可以理解成一个Map，key是n，value是f(n)
if (hasSolvedList.containsKey(n)) {
return hasSolvedList.get(n);
}
int ret = f(n-1) + f(n-2);
hasSolvedList.put(n, ret);
return ret;
}
5.排序(上)——基于比较，O(n^2)：冒泡、插入
912. 排序数组
排序算法的稳定性及其用处
- 多次排序中，下一次排序需要依赖上一次排序的稳定结果。比如订单排序中，先按时间排序，再按价格排序，最终要得到同个价格的订单按下单时间排序，就需要算法稳定性了
冒泡排序
- 对于已经有序的数组，可以提前跳出排序
插入排序（打扑克，插牌）
- 将数组分为有序区间和无序区间
- 每次从无序区间取数，插入有序区间，直到无序区间数据为空
- 重要操作有2：找到合适的位置插入数据和移动其他数据
