CNN（卷积神经网络）入门

 

参考博文：

深度学习基础--卷积--1*1的卷积核与全连接的区别：https://blog.csdn.net/wydbyxr/article/details/84061410

如何理解卷积神经网络中的1*1卷积：https://blog.csdn.net/chaipp0607/article/details/60868689

如何理解卷积神经网络中的权值共享：https://blog.csdn.net/chaipp0607/article/details/73650759

 

本文概述：

　　1. 卷积神经网络简介

　　　　1.1 从传统神经网络到卷积神经网络

　　　　1.2 CNN发展历史

　　2. CNN原理

　　　　2.1 数据输入层(Input layer)(数据预处理)

　　　　2.2 卷积层(卷积+激活)　

　　　　　　2.1.1 卷积如何计算-卷积核大小(1*1, 3*3, 5*5)

　　　　　　2.1.2 卷积如何计算-卷积核步长(stride)

　　　　　　2.1.3 卷积如何计算-卷积核个数

　　　　　　2.1.4 卷积如何计算-卷积核零填充大小(zero-padding)　

　　　　　　  2.1.5 总结-输出大小公式（重要）

　　　　　　2.1.6 激励层（激活层）

　　　　2.3 池化层(下采样层)

　　　　　　2.3.1 池化层计算

　　　　2.4 全连接层

　　3. CNN总结

 

 

1、 卷积神经网络与传统多层神经网络对比

• 传统意义上的多层神经网络是只有输入层、隐藏层、输出层。其中隐藏层的层数根据需要而定，没有明确的理论推导来说明到底多少层合适
• 卷积神经网络CNN，在原来多层神经网络的基础上，加入了更加有效的特征学习部分，具体操作就是在原来的全连接的层前面加入了部分连接的卷积层与池化层。卷积神经网络出现，使得神经网络层数得以加深，深度学习才能实现

通常所说的深度学习，一般指的是这些CNN等新的结构以及一些新的方法（比如新的激活函数Relu等），解决了传统多层神经网络的一些难以解决的问题

传统多层神经网络:

 

卷积神经网络:

 

 

2、CNN发展历史

• 网络结构加深
• 加强卷积功能
• 从分类到检测
• 新增功能模块

2. CNN原理

2.1 数据输入层(数据预处理)

　　有三种常见的数据预处理方法，去均值（demean），归一化，PCA/白化，对于CNN来说，一般只会做去均值+归一化，尤其是我们输入的是图像数据，我们往往只做去均值，这是为了保持原图像数据的完整性，避免失真。图像数据从数学角度来看，就是不同维度的矩阵，经过去均值后，数据的数学特性更好，对称性更好。在我们用SGD（随机梯度下降法）进行迭代优化的时候，权重w(偏差b同理)初始化的随机值对迭代速度和结果没有影响（如果不demean可能会不收敛或者迭代优化速度慢）。

　

 

 　　

 

 

2.2 卷积层(卷积+激活)　　

概述：卷积神经网络三个结构

　　神经网络(neural networks)的基本组成包括输入层、隐藏层、输出层。而卷积神经网络的特点在于隐藏层分为卷积层和池化层(pooling layer，又叫下采样层)以及激活层。每一层的作用

• 卷积层：通过在原始图像上平移来提取特征
• 激活层：增加非线性分割能力
• 池化层：压缩数据和参数的量，减小过拟合，降低网络的复杂度，（最大池化和平均池化）

为了能够达到分类效果，还会有一个全连接层(FC)也就是最后的输出层，计算损失进行分类（或回归）。

 　　对于卷积层，卷积层（Convolutional layer），卷积神经网络中每层卷积层由若干卷积单元(卷积核)组成，每个卷积单元的参数都是通过反向传播算法优化得到的。

卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网路能从低级特征中迭代提取更复杂的特征。

 　　之所以CNN会产生，是因为传统神经网络对于输入的数据X（X视为矩阵）维数太高，如果是一张32x32的灰度图片，一个神经元的权重w就需要32x32，为了提取足够丰富的特征，假设需要20个神经元，则权重W（W视为矩阵）的参数个数就是32x32x20=20480个，显示图片的维度不可能是32，可能是上千，那么W的个数就很容易到上亿，这显然太大了！所以我们需要一种可以显著降低计算量的机制，因此CNN孕育而生！

　　我们直接来说CNN中最重要的卷积核，什么是卷积核，本质就是一个很小的矩阵，如1*1，3*3，5*5等（这里不讨论为啥是这么大，因为我也不知道。。。一般都是大牛经过无数次试验得来的，我们直接借鉴前辈的劳动成果就好）。卷积核会在原数据（很高维的大矩阵）上移动，其实就是一个个小的矩阵，在比它大很多的矩阵上移动（移动的步长一般是1，即一次移动1步），每次移动，做一次点乘，得到一个数字。该步骤会一直进行直至遍历完完整的大矩阵（原数据），如下图。

 

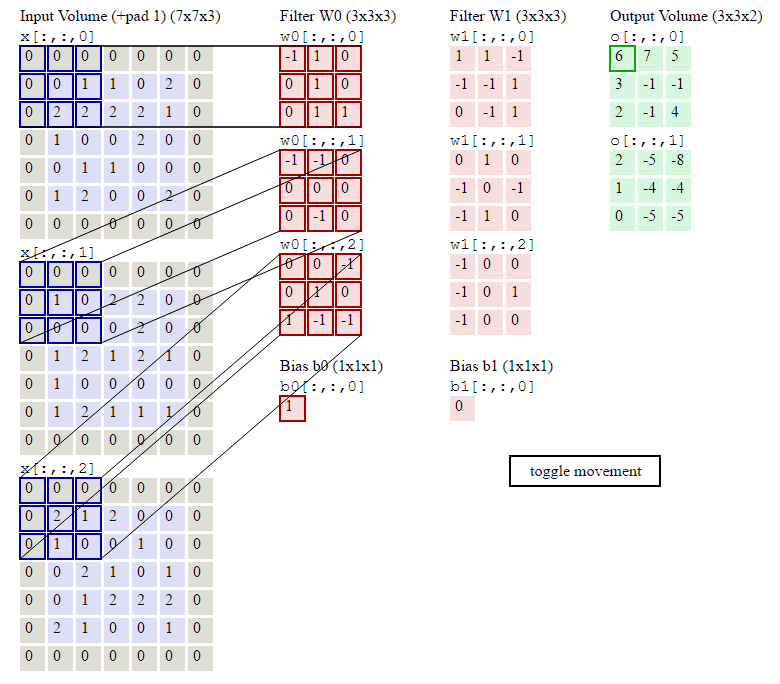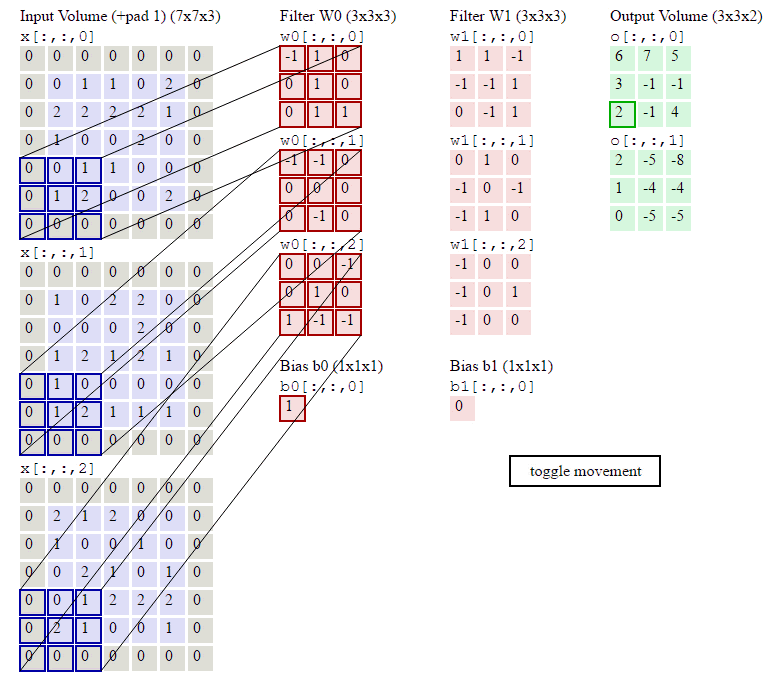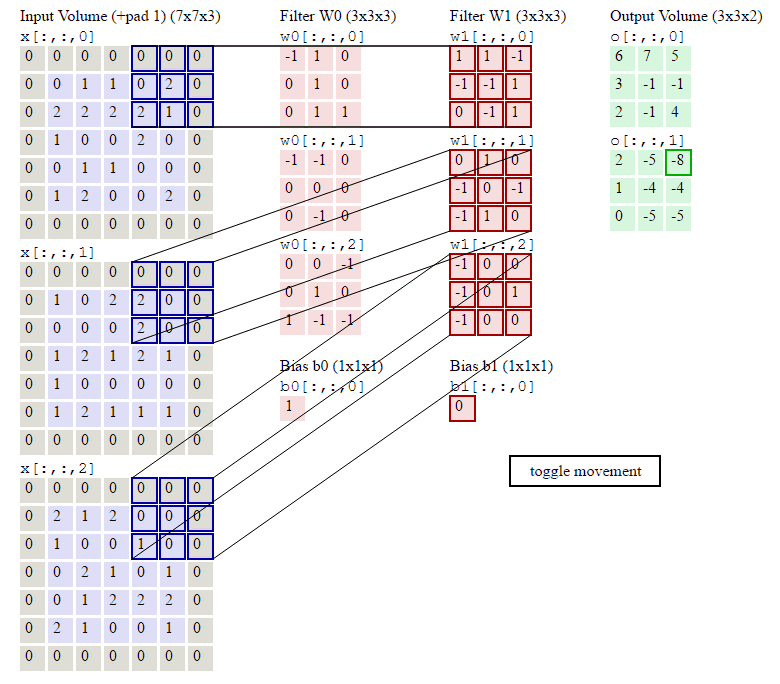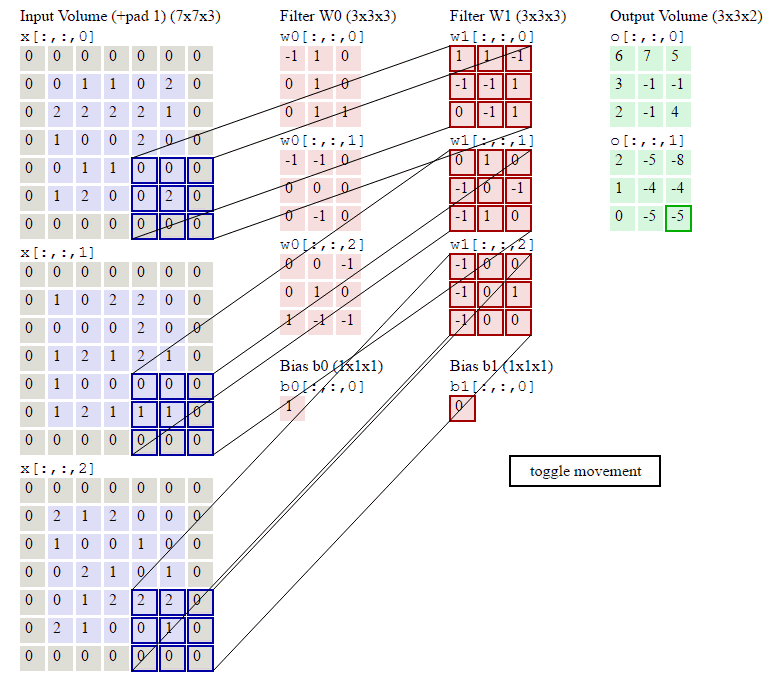
https://blog.csdn.net/chaipp0607/article/details/73650759 （如何理解卷积神经网络中的权值共享）

这里运用了一种思想，我们称之局部关联，或者说是参数共享机制。每个神经元看做一个卷积核（又称之感受野，receptive field），卷积核对局部数据进行计算。其实很简单的理解，所谓参数共享，就是共享卷积核。不管你原来的数据长啥样，我就用这一组卷积核，一直移动计算，仅此而已。这么做的好处就是减少了传统神经网络无法解决的大计算量或者说参数数量太多的问题，并且同样可以提取原数据（如图像数据）的有效特征，并且由于计算量计算参数的减少，特征提取往往做的更好。

卷积操作利用了图片空间上的局部相关性，这也就是CNN与传统神经网络或机器学习的一个最大的不同点，特征的自动提取。 
这也就是为什么卷积层往往会有多个卷积核（甚至几十个，上百个），因为权值共享后意味着每一个卷积核只能提取到一种特征，为了增加CNN的表达能力，当然需要多个核。

　　　

 　　

　　

 

2.1.1 卷积如何计算-卷积核大小(1*1, 3*3, 5*5)

卷积核我们可以理解为一个观察的人，带着若干权重和一个偏置去观察，进行特征加权运算。

注：上述要加上偏置

• 卷积核大小
  • 1*1、3*3、5*5

通常卷积核大小选择这些大小，是经过研究人员证明比较好的效果。这个人观察之后会得到一个运算结果。

 

2.1.2 卷积如何计算-卷积核步长(stride)

需要去移动卷积核观察这张图片，需要的参数就是步长。

假设移动的步长为一个像素，那么最终这个人观察的结果以下图为例：

• 5x5的图片，3x3的卷积大小去一个步长运算得到3x3的大小观察结果

 

如果移动的步长为2那么结果是这样

• 5x5的图片，3x3的卷积大小去两个步长运算得到2x2的大小观察结果

 

 

2.1.3 卷积如何计算-卷积核个数

那么如果在某一层结构当中，不止是一个人观察，多个人(卷积核)一起去观察。那就得到多张观察结果。

• 不同的卷积核带的权重和偏置都不一样，即随机初始化的参数

我们已经得出输出结果的大小有大小和步长决定的，但是只有这些吗，还有一个就是零填充。Filter观察窗口的大小和移动步长会导致超过图片像素宽度！

 

2.1.4 卷积如何计算-卷积核零填充大小(zero-padding)

　　

有两种方式，SAME和VALID

• SAME：越过边缘取样，取样的面积和输入图像的像素宽度一致。
• VALID：不越过边缘取样，取样的面积小于输入人的图像的像素宽度。

在Tensorflow当中，卷积API设置”SAME”之后，输出高宽与输入大小一样（重要）

 

2.1.5 总结-输出大小公式（重要）

最终零填充到底填充多少呢？我们并不需要去关注，接下来我们利用已知的这些条件来去求出输出的大小来看结果

 

计算案例：

1、假设已知的条件：输入图像32*32*1, 50个Filter，大小为5*5，移动步长为1，零填充大小为1。请求出输出大小？

H2 = (H1 - F + 2P)/S + 1 = (32 - 5 + 2 * 1)/1 + 1 = 30

W2 = (H1 - F + 2P)/S + 1 = (32 -5 + 2 * 1)/1 + 1 = 30

D2 = K = 50

所以输出大小为[30, 30, 50]

2、假设已知的条件：输入图像32*32*1, 50个Filter，大小为3*3，移动步长为1，未知零填充。输出大小32*32？

H2 = (H1 - F + 2P)/S + 1 = (32 - 3 + 2 * P)/1 + 1 = 32

W2 = (H1 - F + 2P)/S + 1 = (32 -3 + 2 * P)/1 + 1 = 32

所以零填充大小为：1*1

 

小结：　　

• 1、已知固定输出大小，反过来求出零填充，已知零填充，根据步长等信息，求出输出大小
• 2、卷积层过滤器(卷积核)大小，三个选择1x1，3x3，5x5，步长一般都为1，过滤器个数不定，不同结构选择不同
• 3、每个过滤器会带有若干权重和1个偏置

 

2.1.6 激励层（激活层）

　　作用：把卷积层输出结果做非线性映射

　　激活函数

　　卷积网络结构采用激活函数，自从网路得到发展之后。大家发现原有的sigmoid这些激活函数并不能达到好的效果，所以采取新的激活函数。

3.1 Relu

 

 

 

效果是什么样的呢？

 

 

PS: playground演示不同激活函数作用 http://playground.tensorflow.org/

• Relu
• Tanh
• sigmoid

为什么采取的新的激活函数

• Relu优点
  • 有效解决梯度消失问题
  • 计算速度非常快，只需要判断输入是否大于0。SGD(批梯度下降)的求解速度速度远快于sigmoid和tanh
• sigmoid缺点
  • 采用sigmoid等函数，计算量相对大，而采用Relu激活函数，整个过程的计算量节省很多。在深层网络中，sigmoid函数 反向传播 时，很容易就会出现梯度消失的情况

 

 

 

2.3 池化层(下采样层)

Pooling层主要的作用是压缩数据和参数的量（保持最显著的特征），通过去掉Feature Map中不重要的样本，进一步减少参数数量。Pooling的方法很多，通常采用最大池化

• max_polling:取池化窗口的最大值
• avg_polling:取池化窗口的平均值

2.3.1 池化层计算

池化层也有窗口的大小以及移动步长，那么之后的输出大小怎么计算？计算公式同卷积计算公式一样

计算：224x224x64,窗口为2，步长为2输出结果？

H2 = (224 - 2 + 2*0)/2 +1 = 112

w2 = (224 - 2 + 2*0)/2 +1 = 112

通常池化层采用 2x2大小、步长为2窗口

 

2.4 全连接层（FC, Full Connection层）

前面的卷积和池化相当于做特征工程，最后的全连接层在整个卷积神经网络中起到“分类器”的作用（如果FC层作为最后一层，再加上softmax或者wx+b，则可以分别作为分类或回归的作用，即“分类器”或“回归器”的作用）；如果作为倒数第2，3层的话，FC层的作用是信息融合，增强信息表达。

 

3. CNN总结

• 优点
  • 共享卷积核，优化计算量
  • 无需手动选取特征，训练好权重，即得特征
  •  深层次的网络抽取图像信息丰富，表达效果好
• 缺点
  • 需要调参，需要大样本量， GPU等硬件依赖
  • 物理含义不明确（可解释性不强）