数据结构——并查集

·艹并查集算数据结构吗那么水一玩意儿应该不算但给它放进去吧

下午考试求rp++

 

一、并查集介绍

·并查集是一种树型的数据结构，用于处理一些不相交集合的合并问题。
·并查集的主要操作有
1－合并两个不相交集合
2－查看两个元素是否属于同一个集合

二、并查集操作过程

·判断元素是否属于同一集合

用某个元素所在树的根结点表示该元素所在的集合
判断两个元素时候属于同一个集合的时候，只需要判断他们所在树的根结点是否一样即可
当我们合并两个集合的时候，只需要在两个根结点之间连边即可

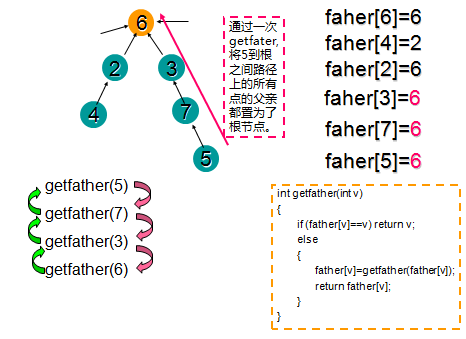
 ·具体方法：路径压缩

判断元素是否属于同一集合
用某个元素所在树的根结点表示该元素所在的集合
判断两个元素时候属于同一个集合的时候，只需要判断他们所在树的根结点是否一样即可
当我们合并两个集合的时候，只需要在两个根结点之间连边即可

 由此我们得到了一个复杂度只是O(1)的算法来判断两个元素是否位于同一集合

故查询同时进行路径压缩

int getfather(int v) //查阅元素v的父亲，即查看元素v所在集合的根节点
{
       if (father[v]==v) return v;  //v本身为根节点
       else
       {
		    father[v]=getfather(father[v]);
             return father[v];
       }
}

·判断两个元素是否位于同一集合,如果不在同一集合，合并两个集合：

bool Merge(int x,int y)
{
        int  fx,fy ;
        fx = getfather(x);
        fy = getfather(y);
        if (fx==fy) return true;
        else 
        {
                 father[fx] = fy; //合并两个集合
                 return false;
        }
}

·并查集模板：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int fa[30005];
int n,m,z,x,y;
int getfather(int v)
{
	if(fa[v]==v) return v;
	else
	{
		fa[v]=getfather(fa[v]);
		return fa[v];
	}
}
void merge(int x,int y)
{
	int fx=getfather(x);
	int fy=getfather(y);
	fa[fx]=fy;
}
int main()
{
	cin>>n>>m;
	for(int i=1;i<=30000;i++) fa[i]=i;
	for(int i=1;i<=m;i++)
	{
		cin>>z>>x>>y;
		if(z==1)
		{
			merge(x,y);
		}
		else
		{
			if(getfather(x)!=getfather(y)) cout<<"N"<<endl;
			else
			{
				cout<<"Y"<<endl;
			}
			
		}
	}
	return 0;
}　　

---

 

二、并查集之with求值

用一道例题引入：

[USACO04OPEN]Cube Stacking 方块游戏https://www.luogu.org/problem/P5092　

题目内容：

·分析：

·板子：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int p;
string s;
const int maxn=100005;
int before[maxn],count[maxn],father[maxn];
int getfather(int x)
{
	int dad;
	if(x==father[x]) return x;
	dad=getfather(father[x]);
	before[x]+=before[father[x]];
	father[x]=dad;
	return father[x];
}
void merge(int x,int y)
{
	x=getfather(x);
	y=getfather(y);
	father[y]=x;
	before[y]+=count[x];
	count[x]+=count[y]; 
}
//此只保证了根节点count正确 
int main()
{
	cin>>p;
	int a,b,c;
	for(int i=1;i<=30000;i++) father[i]=i;
	for(int i=1;i<=30000;i++) count[i]=1;
	for(int i=1;i<=p;i++)
	{
		cin>>s;
		if(s=="M")
		{
			cin>>a>>b;
			merge(a,b);
		}
		else 
		{
			cin>>c;
			int fc=getfather(c);
			cout<<count[fc]-before[c]-1<<endl;
		}
		
	}
	return 0;
}　　

---

 

下面附一道难题：

 

·板子：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
using namespace std;
int n,q;
struct node{
	char type;
	int k;
	int a,b,v;
	int l[30];
}; 
node work[50005];
int father[50005];
int w[50005];
int getfather(int x){
	if(x!=father[x]){
		int root=getfather(father[x]);
		w[x]^=w[father[x]];
		return father[x]=root;
	}
	else return x;
}
void solve(){
	int i,j,k;
	int cnt=0,ans=0;
	int vis[50005];
	memset(vis,0,sizeof(vis));
	bool flag=true;
	for(i=1;i<=q;i++){
		if(work[i].type=='I'){
			cnt++;
			int fx=getfather(work[i].a);
			int fy=getfather(work[i].b);
			if(fx==n)swap(fx,fy);
			if(fx==fy){
				if((w[work[i].a]^w[work[i].b])!=work[i].v){
					printf("The first %d facts are conflicting.\n",cnt);  
            		return;
				}
			}
			else{
				father[fx]=fy;
				w[fx]=(w[work[i].a]^w[work[i].b]^work[i].v);
			}
		}
		else{
			memset(vis,0,sizeof(vis));
			ans=0;
			flag=true;
			for(j=1;j<=work[i].k;j++){
				int fx=getfather(work[i].l[j]);
				if(fx!=n)vis[fx]^=1;
				ans^=w[work[i].l[j]];
			}
			for(j=1;j<=work[i].k;j++){
				if(vis[father[work[i].l[j]]]){
					flag=false;
				}
			}
			if(flag)printf("%d\n",ans);
			else printf("I don't know.\n");
		}
	}
}
int main(){
	int Case=0;
	while(cin>>n>>q&&n!=0&&q!=0){
		printf("Case %d:\n",++Case); 
		memset(work,0,sizeof(work));
		memset(father,0,sizeof(father));
		memset(w,0,sizeof(w));
		int i,j,k;
		char s[1005];
		for(i=0;i<=n;i++)father[i]=i;
		for(i=1;i<=q;i++){
			int a,b,v;
			scanf("%s",s);
			work[i].type=s[0];
			if(s[0]=='I'){
				gets(s);
				if(sscanf(s,"%d%d%d",&a,&b,&v)==2){
					v=b;
					b=n;
				}
				work[i].a=a;work[i].b=b;work[i].v=v;
			}
			else if(s[0]=='Q'){
				scanf("%d",&work[i].k);
				for(j=1;j<=work[i].k;j++){
					scanf("%d",&work[i].l[j]);
				}
			}
		}
		solve();
		puts("");
	}
}