SparkMLlib-----GMM算法
Gaussian Mixture Model(GMM)是一个很流行的聚类算法。它与K-Means的很像,但是K-Means的计算结果是算出每个数据点所属的簇,而GMM是计算出这些数据点分配到各个类别的概率。与K-Means对比K-Means存在一些缺点,比如K-Means的聚类结果易受样本中的一些极值点影响。此外GMM的计算结果由于是得出一个概率,得出一个概率包含的信息量要比简单的一个结果多,对于49%和51%的发生的事件如果仅仅使用简单的50%作为阈值来分为两个类别是非常危险的。
Gaussian Mixture Model,顾名思义,它是假设数据服从高斯混合分布,或者说是从多个高斯分布中生成出来的。每个GMM由K个高斯分布组成,每个高斯分布称为一个"Component",这些Component线性加在一起就组成了GMM的概率密度函数:
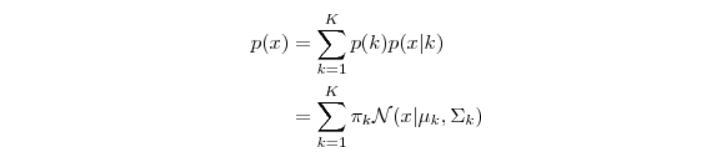
使用GMM做聚类的方法,我们先使用R等工具采样数据绘出数据点分布的图观察是否符合高斯混合分布,或者直接假设我们的数据是符合高斯混合分布的,之后根据数据推算出GMM的概率分布,对应的每个高斯分布就是每个类别,因为我们已知(假设)了概率密度分布的形式,要去求出其中参数,所以是一个参数估计的过程,我们要推导出每个混合成分的参数(均值向量mu,协方差矩阵sigma,权重weight),高斯混合模型在训练时使用了极大似然估计法,最大化以下对数似然函数:
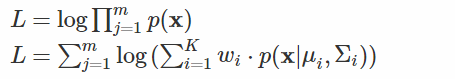
该式无法直接解析求解,因此采用了期望-最大化方法(Expectation-Maximization,EM)方法求解,具体步骤如下:
1.根据给定的K值,初始化K个多元高斯分布以及其权重;
2.根据贝叶斯定理,估计每个样本由每个成分生成的后验概率;(EM方法中的E步)
3.根据均值,协方差的定义以及2步求出的后验概率,更新均值向量、协方差矩阵和权重;(EM方法的M步)重复2~3步,直到似然函数增加值已小于收敛阈值,或达到最大迭代次数
接下来进行模型的训练与分析,我们采用了mllib包封装的GMM算法,具体代码如下
package com.xj.da.gmm
import breeze.linalg.DenseVector
import breeze.numerics.sqrt
import org.apache.commons.math.stat.correlation.Covariance
import org.apache.spark.mllib.clustering.{GaussianMixture, GaussianMixtureModel}
import org.apache.spark.mllib.linalg
import org.apache.spark.mllib.linalg.distributed.RowMatrix
import org.apache.spark.mllib.linalg.{Matrices, Matrix, Vectors}
import org.apache.spark.mllib.stat.distribution.MultivariateGaussian
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}
import scala.collection.mutable.ArrayBuffer
/**
* author : kongcong
* number : 27
* date : 2017/7/19
*/
object GMMWithMultivariate {
def main(args: Array[String]): Unit = {
val conf = new SparkConf()
//.setMaster("local")
.setAppName("GMMWithMultivariate")
val sc = new SparkContext(conf)
val rawData: RDD[String] = sc.textFile("hdfs://master:8020/home/kongc/data/query_result.csv")
//val rawData: RDD[String] = sc.textFile("data/query_result.csv")
println("count: " + rawData.count())
//println(rawData.count())
// col1, col2, status
val data: RDD[linalg.Vector] = rawData.map { line =>
val raw: Array[String] = line.split(",")
Vectors.dense(raw(0).toDouble, raw(1).toDouble, raw(4).toDouble)
}
// data.collect().take(10).foreach(println(_))
// col1, col2, status
val trainData: RDD[linalg.Vector] = rawData.map { line =>
val raw: Array[String] = line.split(",")
Vectors.dense(raw(0).toDouble, raw(1).toDouble)
}
// trainData.collect().take(10).foreach(println(_))
// 指定初始模型
// 0
val filter0: RDD[linalg.Vector] = data.filter(_.toArray(2) == 0)
println(filter0.count()) //23195
// 1
val filter1: RDD[linalg.Vector] = data.filter(_.toArray(2) == 1)
println(filter1.count()) //14602
val w1: Double = (filter0.count()/319377.toDouble)
val w2: Double = (filter1.count()/319377.toDouble)
println(s"w1 = $w1")
// 均值
val m0x: Double = filter0.map(_.toArray(0)).mean()
val m0y: Double = filter0.map(_.toArray(1)).mean()
val m1x: Double = filter1.map(_.toArray(0)).mean()
val m1y: Double = filter1.map(_.toArray(1)).mean()
// 方差
val vx0: Double = filter0.map(_.toArray(0)).variance()
val vy0: Double = filter0.map(_.toArray(1)).variance()
val vx1: Double = filter1.map(_.toArray(0)).variance()
val vy1: Double = filter1.map(_.toArray(1)).variance()
// 均值向量
val mu1: linalg.Vector = Vectors.dense(Array(m0x, m0y))
val mu2: linalg.Vector = Vectors.dense(Array(m1x, m1y))
println(s"mu1 : $mu1")
println(s"mu2 : $mu2")
val array: RDD[Array[Double]] = rawData.map { line =>
val raw: Array[String] = line.split(",")
Array(raw(0).toDouble, raw(1).toDouble, raw(4).toDouble)
}
val f0: RDD[Array[Double]] = array.filter(_(2) == 0)
val f1: RDD[Array[Double]] = array.filter(_(2) == 1)
println("f0.count:"+f0.count())
println("f1.count:"+f1.count())
// 0 x,y求协方差矩阵
val x0: RDD[Double] = f0.map(_(0))
val y0: RDD[Double] = f0.map(_(1))
//println(x0.collect().length == y0.collect().length)
// 1 x,y求协方差矩阵
val x1: RDD[Double] = f1.map(_(0))
val y1: RDD[Double] = f1.map(_(1))
val ma0: Array[Array[Double]] = Array(x0.collect(),y0.collect())
val ma1: Array[Array[Double]] = Array(x1.collect(),y1.collect())
val r0: RDD[Array[Double]] = sc.parallelize(ma0)
val r1: RDD[Array[Double]] = sc.parallelize(ma1)
val rdd0: RDD[linalg.Vector] = r0.map(f => Vectors.dense(f))
val rdd1: RDD[linalg.Vector] = r1.map(f => Vectors.dense(f))
val RM0: RowMatrix = new RowMatrix(rdd0)
val RM1: RowMatrix = new RowMatrix(rdd1)
// 计算协方差矩阵
//println(RM0.computeCovariance().numCols)
/*val i: Double = DenseVector(1.0, 2.0, 3.0, 4.0) dot DenseVector(1.0, 1.0, 1.0, 1.0)
val c0yx: Double = i - m0x * m0y*/
val c0yx: Double = DenseVector(x0.collect()) dot DenseVector(y0.collect()) - m0x * m0y
val c1yx: Double = DenseVector(x1.collect()) dot DenseVector(y1.collect()) - m1x * m1y
//cov(Vectors.dense(x0.collect()),Vectors.dense(y0.collect()))
val sigma1 = Matrices.dense(2, 2, Array(vx0, c0yx, c0yx, vy0))
val sigma2 = Matrices.dense(2, 2, Array(vx1, c1yx, c1yx, vy1))
val gmm1 = new MultivariateGaussian(mu1, sigma1)
val gmm2 = new MultivariateGaussian(mu2, sigma2)
val gaussians = Array(gmm1, gmm2)
// 构建一个GaussianMixtureModel需要两个参数 一个是权重数组 一个是组成混合高斯分布的每个高斯分布
val initModel = new GaussianMixtureModel(Array(w1, w2), gaussians)
for (i <- 0 until initModel.k) {
println("weight=%f\nmu=%s\nsigma=\n%s\n" format
(initModel.weights(i), initModel.gaussians(i).mu, initModel.gaussians(i).sigma))
}
val gaussianMixture = new GaussianMixture()
val mixtureModel = gaussianMixture
.setInitialModel(initModel)
.setK(2)
.setConvergenceTol(0.0001)
.run(trainData)
val predict: RDD[Int] = mixtureModel.predict(trainData)
rawData.zip(predict).saveAsTextFile("hdfs://master:8020/home/kongc/data/out/gmm/predict2")
for (i <- 0 until mixtureModel.k) {
println("weight=%f\nmu=%s\nsigma=\n%s\n" format
(mixtureModel.weights(i), mixtureModel.gaussians(i).mu, mixtureModel.gaussians(i).sigma))
}
}
}
参考:http://blog.pluskid.org/?p=39
http://dblab.xmu.edu.cn/blog/1456/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号