线段相交的判断

第一种方法是：判断这两个直线是否相交，相交并且交点在线段上，就可以保证两个线段是相交的。

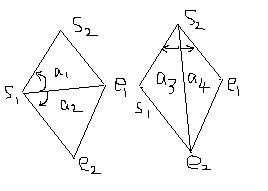
第二种方法是：跨立算法。属于计算几何的一个基础。保证几个有向面积是相反的即可。是充要条件。知道三个点计算一个三角形的有向面积就是一个三阶的最后一列为1的行列式的求值。

这里用第二种方法：

 

import java.awt.Paint;

public class SetmentTest {

    // 参考文献 https://www.2cto.com/kf/201404/296319.html
    public static double get_area(Point a0, Point a1, Point a2) {
        double s = a0.x * a1.y + a2.x * a0.y + a1.x * a2.y - a2.x * a1.y - a0.x * a2.y - a1.x * a0.y;
        return s;
    }

    public static boolean segmentIntersect(Point st1, Point ed1, Point st2, Point ed2) {
        double s1 = get_area(st1, ed1, st2);
        double s2 = get_area(st1, ed1, ed2);
        double s3 = get_area(st2, ed2, st1);
        double s4 = get_area(st2, ed2, ed1);
        if (s1 * s2 <= 0 && s3 * s4 <= 0) {
            // System.out.println("Intersection\n");
            return true;
        } else {
            // System.out.println("No Intersection");
            return false;
        }
    }

    public static void main(String[] args) {
        Point aa = new Point(1, 1);
        Point bb = new Point(2, 2);
        Point cc = new Point(1, 2);
        Point dd = new Point(2, 1);
        System.out.println(SetmentTest.segmentIntersect(aa, bb, cc, dd));
        if (SetmentTest.segmentIntersect(aa, bb, cc, dd) == true)
            System.out.println("有交点");
        else
            System.out.println("没有交点");

    }

}

 

参考文献：

• https://blog.csdn.net/wingrez/article/details/75042006
• http://www.cnblogs.com/jbelial/archive/2011/08/04/2127487.html
• https://blog.csdn.net/k_koris/article/details/81711396?utm_source=blogxgwz4
• https://www.2cto.com/kf/201404/296319.html