回溯法、子集树、排列树、满m叉树

显示图：

明确给出了图中的各顶点及边

隐式图：

仅给出初始节点、目标节点及产生子节点的条件（一般有问题提议隐含给出）的情况下，构造一个图。

回溯法：

从初始状态出发，在隐式图中以深度优先的方式搜索问题的解。当发现不满足求解条件时，就回溯，尝试其他路径。通俗的说，回溯法就是一种能进则进，进不了就换，换不了就退的基本搜索方法。

 

回溯法的算法框架和思想:

1、回溯法的算法框架及思想

回溯法是一种搜索算法，解决问题时，首先应明确搜索范围，即问题所有可能解的组成范围、这个范围越小越好，且至少包含问题的一个(最优)解。 为了定义搜索范围，需要明确以下几个方面:

（1）问题解的形式:回溯法看重问题的解能够表示成一个n元组(x1,x2...xn)的形式。

（2）显约束：对分量xi(i=1,2...n)的取值范围限定。

（3）隐约束:为满足问题的解而对不同分量之间施加的约束。

（4）解空间:对于问题的一个实例，解向量满足显约束的所有n元组构成了该实例的一个解空间。

注意:同一个问题的显约束可能有多种，相应解空间的大小就会不同，通常情况下，解空间越小，算法效率越高。

 

子集树：

子集树是使用回溯法解题时经常遇到的一种典型的解空间树。

子集树中所有非叶子节点均有左右两个分支，我们一般设定左分支为1，右分支为0。树的根结点表示初始状态，中间节点表示某种情况下的中间状态，叶子节点表示结束状态。分支表示从一个状态过度到另一个状态的行为。从根节点到叶结点的路径表示一个可能解。

示例：

从n个元素中选取一些元素

• 这类子集树通常有2ⁿ个叶结点，其结点总个数为2ⁿ⁺¹-1。
• 遍历子集树的任何算法均需O(2ⁿ)的计算时间。

子集树形式：（下面以n==3为例）

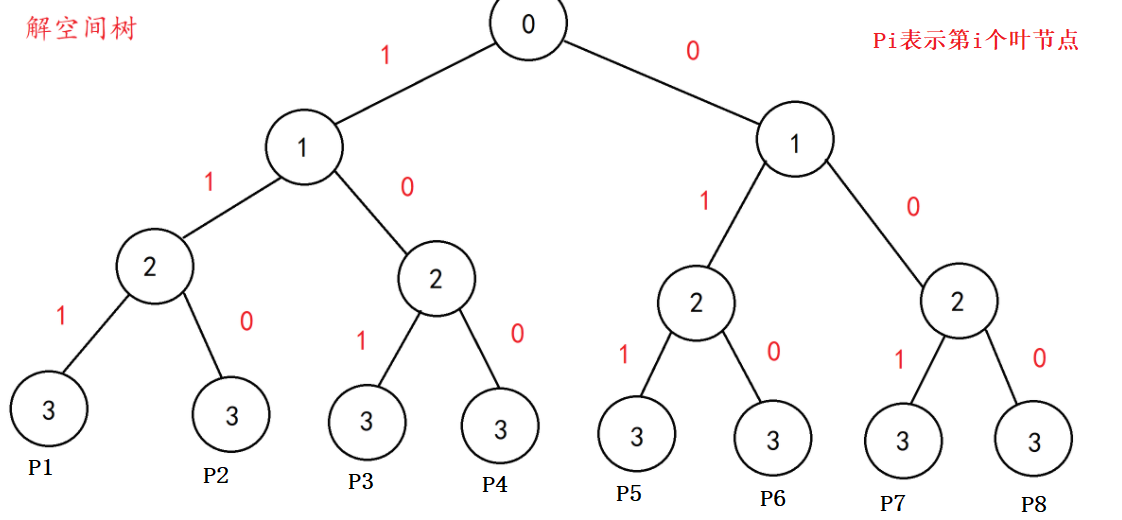
对于根节点0号元素，它有两个分支，左边是1，右边是0。左边就代表我们会选择第0号元素，右边就代表我们不选取第0号元素。之后的类似。

对于叶节点P1表示：3个元素都选

对于叶节点P2表示：选取元素编号为：0，1

对于叶节点P3表示：选取元素编号为：0，2

......

 

 

排列树：

排列树是用回溯法解题时经常遇到的第二种典型的解空间树。

当所给的问题是从n个元素的排列中找到满足某种性质的一个排列时，相应的解空间树就是排列树。

 

• 排列树通常有n!个叶结点。
• 因此遍历排列树需要O(n!)的计算时间

 

示例：

给你3个元素（1，2，3），它的排列树如下：

从根节点A，到它的子节点B、C、D这个路径是来选择第一个元素，走到B节点代表第一个元素选取的是1，走到C节点代表第一个元素选取的是2，后面的类似

 

 

满m叉树：

满m叉树是用回溯法解题时经常遇到的第三种典型的解空间树，也称为组合树。

当所给问题的n个元素中每一个元素均有m种选择，要求确定其中的一种选择，使得对这n个向量的选择结果组成的向量满足某种性质。

n==3的m叉树

 

 

 

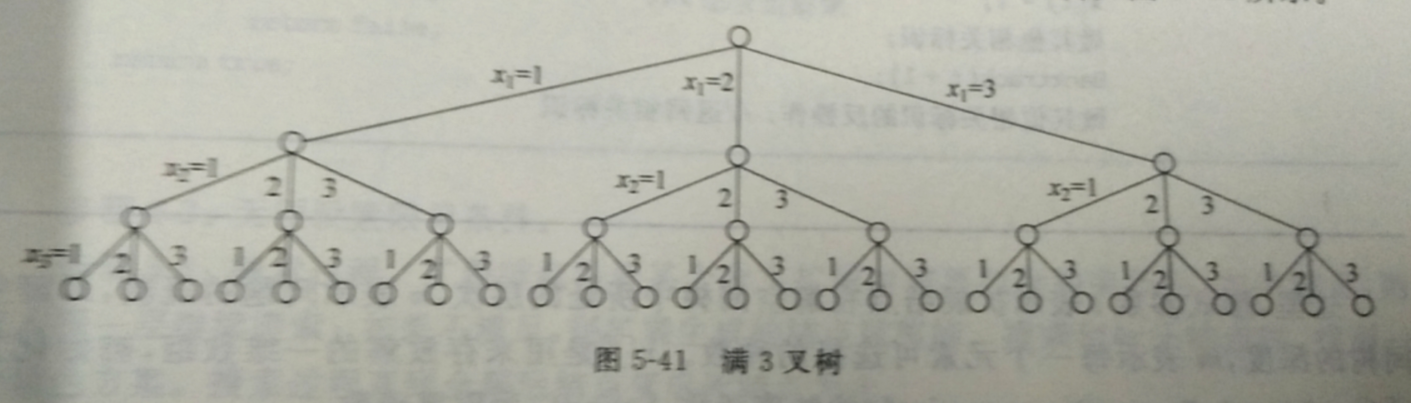
除了叶节点之外，每一个节点都有3个子节点，这就代表的3种选择