最优二叉查找树

最优二叉树也就是哈夫曼树，最优二叉树和最优二叉查找树是不一样的。我们说一下他们的定义

 

最优二叉树：

给你n个节点，每一个节点有一个权值wi。我们设一棵树的权值是所有节点的权值乘于每一个节点的深度，但是我们可以构造出来许多二叉树，我们称构造出来的那个权值最小的二叉树就是我们找的最优二叉树

 

求解最优二叉树：

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)；

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

 

 

最优二叉查找树：

给定n个节点的值key，假设x是二叉搜索树中的一个结点。如果L是x的左子树的一个结点，那么L.key ≤ x.key。如果R是x的右子树的一个结点，那么R.key ≥ x.key。使用<key1,key2,key3....keyn>表示，且我们设定key1<key2<key3<keyn。

对于n个节点都有一个访问概率pi，使用<p1,p2,p3....pn>表示。还有未找到访问点概率qi，我们使用<q0,q1,q2,q3....qn>表示。

例如访问到[-∞,key1)的概率是q0，访问到(key1,key2)的概率是q1，，，，访问到(keyn,∞)的概率是qn。

我们设定[-∞,key1)区间为d0，(key1,key2)区间为d1，，，，(keyn,∞)区间是dn。

所以是不会出现对于i,j(1<=i,j<=n)满足keyi==keyj的情况出现

 

我们需要把2*n+1个节点放在一个二叉树上，其中n个节点是keyi，还有n+1个节点di。

最后形成的二叉树中叶节点肯定是di。且∑ⁿ_i=1pi+∑ⁿ_i=0qi=1

 

假定一次搜索的代价等于访问的结点数，也就是此次搜索找到的结点在二叉搜索树中的深度再加1。给定一棵二叉搜索树T，我们可以确定进行一次搜索的期望代价如下：

其中depth_T​表示一个结点在二叉搜索树T中的深度。

E = ∑ⁿ_i=1 （depth_T(keyi)+1）*pi  +  ∑ⁿ_i=0（depth_T(di)+1）*qi

　= 1 + ∑ⁿ_i=1 （depth_T(keyi)）*pi  +  ∑ⁿ_i=0（depth_T(di)）*qi

 

我们要找到那个期望E最小的满足题意二叉树，这就是最优二叉查找树

 

最优二叉树是符合最优子结构的，假设由关键字子序列<keyi,keyi+1,,,,keyj>和伪关键字子序列<di-1,di,di+1,,,,,dj>构成的一棵最优二叉搜索树以k_r ( i ≤ r ≤ j )为根结点。那么它的左子树由子序列<keyi,,,,keyr-1>和<di-1,,,,dr-1>构成，这颗左子树显然也是一棵最优二叉搜索树。同样，它的右子树由子序列<keyr+1,,,,keyj>和<dr,,,,dj>构成，这颗右子树显然也是一棵最优二叉搜索树。

 

注意一下空子树，也就是由关键字<keyi,keyj>,且当选keyi为根节点的时候，它的左子树<keyi,keyi-1>就只包含di-1，同理选keyj为根节点时，右子树只包含dj。

用e[i,j]表示包含关键字子序列<keyi,keyi+1,,,,keyj>的最优二叉搜索树的期望搜索代价。我们最终希望计算出e[1,n]。

 

当j=i-1时，说明此时只有d_i-1，故e[i,i-1] = q_i-1

当j≥i时，需要从k_i，……，k_j中选择一个跟k_r，然后用关键字k_i，……，k_r-1来构造一棵最优二叉查找树作为左子树，用关键字k_r+1，……，k_j来构造一棵最优二叉查找树作为右子树。定义一棵有关键字k_i，……，k_j的子树，定义概率的总和为：

 

 

 

因此如果k_r是一棵包含关键字k_i，……，k_j的最优子树的根，则有：

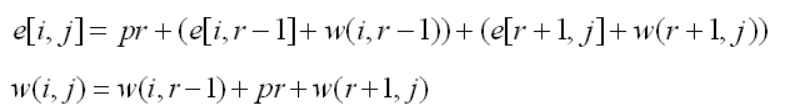
整理得：

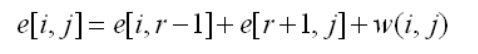
最终递推式：

 

 

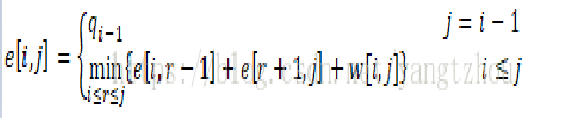
e[i,j]给出了最优二叉搜索树子问题的期望搜索代价。我们还需要记录最优二叉搜索树子问题的根结点，用root[i,j]来记录。

给出伪代码：

 

 

 

 

代码：

#include<iostream>
using namespace std;

const int MAX=9999999;
//const int N=5;  //这是第一个例子
//float p[N+1]={0,0.15,0.10,0.05,0.1,0.20};
//float q[N+1]={0.05,0.10,0.05,0.05,0.05,0.10};
const int N=7;    //这是第二个例子
float p[N+1]={0.04 ,0.06, 0.08, 0.02, 0.10, 0.12, 0.14};
float q[N+1]={0.06 ,0.06, 0.06, 0.06, 0.05, 0.05, 0.05,    0.05};

float e[N+2][N+1];
int root[N+1][N+1];
float w[N+2][N+1];

void optimal_bst_search_tree(float p[],float q[],int n)
{
    int i;
    for(i=1;i<=n+1;i++)
    {
        e[i][i-1]=q[i-1];
        w[i][i-1]=q[i-1];
    }
    int l,j,r;
    for(l=1;l<=n;l++)  //枚举区间长度，也就是e[i][j]的j-i+1的长度
    {
        for(i=1;i<=n-l+1;i++)
        {
            j=i+l-1;
            e[i][j]=MAX;
            w[i][j]=w[i][j-1]+p[j]+q[j];
            for(r=i;r<=j;r++)
            {
                double t=e[i][r-1]+e[r+1][j]+w[i][j];
                if(t<e[i][j])
                {
                    e[i][j]=t;
                    root[i][j]=r;
                }
            }
        }
    }
}

void print_root()
{
    int i,j;
    cout<<"各子树的根："<<endl;
    for(i=1;i<=N;i++)
    {
        for(j=1;j<=N;j++)
            cout<<root[i][j]<<" ";
        cout<<endl;
    }
}

void construct_optimal_bst(int i,int j)
{
    if(i<=j)
    {
        int r=root[i][j];
        cout<<r<<" ";
        construct_optimal_bst(i,r-1);
        construct_optimal_bst(r+1,j);
    }
}
void print_bst(int i,int j)
{
    if(i==1&&j==N)
        cout<<"root is "<<root[i][j]<<endl;
    if(i<j)
    {
        int r=root[i][j];
        if(i!=r)
            cout<<"left child root "<<root[i][r-1]<<endl;
        print_bst(i,root[i][j]-1);
        if(j!=r)
            cout<<"right child root "<<root[r+1][j]<<endl;
        print_bst(root[i][j]+1,j);
    }
}
int main()
{
    optimal_bst_search_tree(p,q,N);
    print_root();
    cout<<"构造的最优二叉树："<<endl;
    construct_optimal_bst(1,5);
    cout<<endl;
    print_bst(1,N);
    return 0;
}
//0.04 ,0.06, 0.08, 0.02, 0.10, 0.12, 0.14
//0.06 0.06 0.06 0.06 0.05 0.05 0.05    0.05

 

第二个例子的最优二叉查找树如下：算出来期望是3.12