POJ1113:Wall (凸包算法学习）

题意：

给你一个由n个点构成的多边形城堡（看成二维），按顺序给你n个点，相邻两个点相连。

让你围着这个多边形城堡建一个围墙，城堡任意一点到围墙的距离要求大于等于L，让你求这个围墙的最小周长（看成二维平面）（结果四舍五入

 

分析：

凸包问题和这个问题的差别就在于：凸包问题没有“城堡任意一点到围墙的距离要求大于等于L”这个要求

凸包：找到一个凸多边形把这n个点形成的多边形围起来，找到的那个周长最小的凸多边形就是我们所求的凸包

那么这个问题怎么在凸包的基础上解决呢？

我们考虑L，对于求出的凸多边形，对于它的顶点X，可以证明每个X附近需要增加一定的圆弧来保证顶点到圆弧的距离大于等于L，

所有X的圆弧角度之和为Pi，将凸包平移与圆弧连接成封闭图案，最终 ans=凸包+2*Pi*L。如下图（参考：https://my.oschina.net/u/4331110/blog/4250115）

 

 

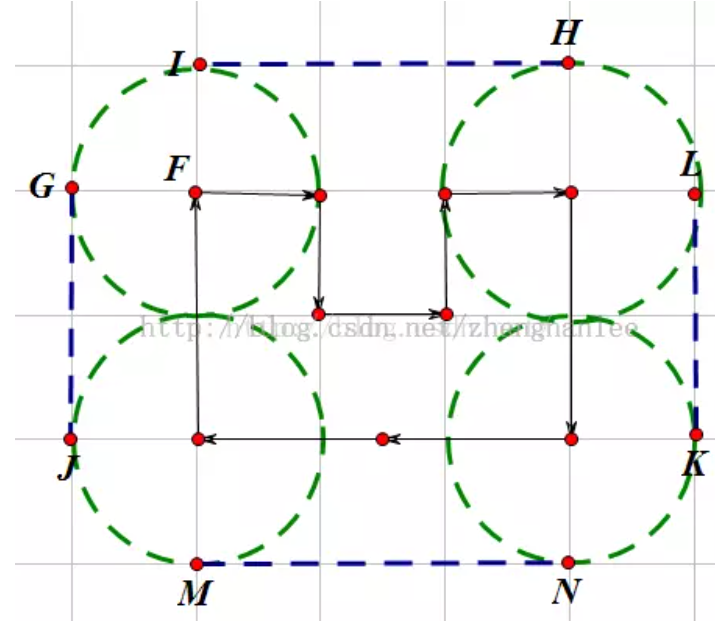
上图中黑色实线连起来的多边形就是题目给出的n个点形成的多边形

我们就是要在这个基础上满足题目“城堡任意一点到围墙的距离要求大于等于L”要求

如上图所示，也就只需要多加4段圆弧就可以满足题目需求，答案也就是ans=凸包+2*Pi*L

 

 

凸包怎么求（参考：https://www.cnblogs.com/czaoth/p/6912073.html）？

这里我们使用Graham Scan算法来实现，此算法能够在O(nlogn)的时间内找到凸包。

 

这里说一下二维平面下叉积的几何意义：对于二维向量a=(x1,y2)和b=(x2,y2)，a×b定义为x1*y2-y1*x2。而它的几何意义就是|a||b|sin<a,b>。如果a与b夹角小于180度（逆时针），那么这个值就是正值，大于180度就是负值。需要注意的是，左乘和右乘是不同的。这里给出几个例子

 

 

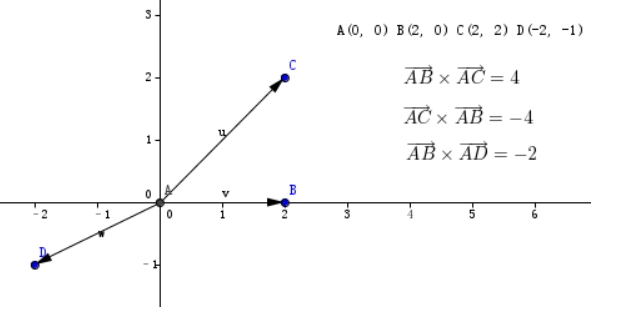
我认为这个sin<a,b>就是：a向量按照逆时针移动到b向量同方向的角度

 

Graham Scan算法过程：

Graham Scan算法的做法是先定下一个起点，一般是最左边的点和最右边的点（需要排序后选择起点），然后一个个点扫过去，如果新加入的点和之前已经找到的点所构成的“壳”凸性没有变化，就继续扫，否则就把已经找到的最后一个点删去，再比较凸性，直到凸性不发生变化。分别扫描上下两个“壳”，合并在一起，凸包就找到了。

我们找下“壳”，上下其实是一样的。首先加入两个点A和C：

 

 

然后插入第三个点G，并计算AC×CG的叉积，却发现叉积小于0，也就是说逆时针方向上∠ACG大于180度，于是删去C点，加入G点：

 

 

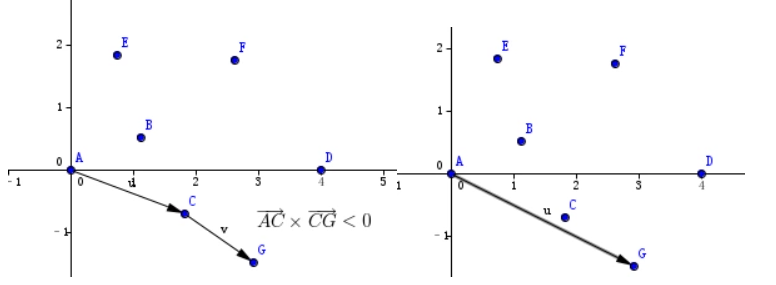
然后就是依照这个步骤便能加入D点。在AD上方是以D为起点。就能够找到AGD和DFEA两个凸壳。合并就得到了凸包。

 

 

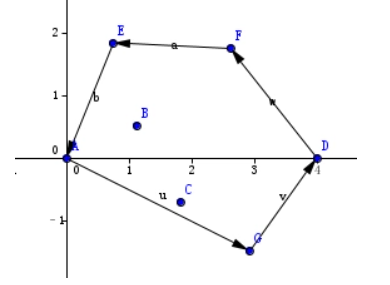
关于扫描的顺序，有坐标序和极角序两种。坐标序是比较两个点的x坐标，如果小的先被扫描（扫描上凸壳的时候反过来）；如果两个点x坐标相同，那么就比较y坐标，小的先被扫描（扫描上凸壳的时候也是反过来）。极角序使用arctan2函数的返回值进行比较

 

给出POJ1113:Wall代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<queue>
#include<stack>
#include<map>
#include<math.h>
using namespace std;
const int maxn=1e3+10;
const double PI=acos(-1.0);  //180度的弧度制
const double eps=1e-6;
struct Cpoint
{
    double x,y;
    Cpoint(){}
    Cpoint(double xx,double yy):x(xx),y(yy){}
    Cpoint friend operator -(Cpoint a,Cpoint b)
    {
        return Cpoint(a.x-b.x,a.y-b.y);
    }
    double friend operator ^(Cpoint a,Cpoint b)
    {
        return a.x*b.y-b.x*a.y;
    }
    bool friend operator <(Cpoint a,Cpoint b)
    {
        if(a.y==b.y) return a.x<b.x;
        return a.y<b.y;
    }
}point[maxn];
double dist(Cpoint a,Cpoint b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
int Sign(double x)
{
    if(x>=-eps && x<=eps) return 0;
    if(x>eps) return 1;
    else return -1;
}
bool cmp(Cpoint a,Cpoint b)
{
    int s=Sign((a-point[1])^(b-point[1]));
    if(s>0 || (s==0 && dist(a,point[1])<dist(b,point[1]))) return 1;
    else return 0;
}
int n,l;
double Graham()
{
    double res=0;
    sort(point+1,point+1+n); //得到原点（原点一般让两端的点来当）
    sort(point+1,point+1+n,cmp); //得到积角序
    int que[maxn],top=3;
    que[1]=1;
    que[2]=2;
    que[3]=3;
    for(int i=4;i<=n;++i)
    {        //注意下面点的顺序不要写错了 
        while(top>1 && Sign((point[que[top]]-point[que[top-1]])^(point[i]-point[que[top]]))<=0)
            top--;
        que[++top]=i;
        
    }
    for(int i=1;i<top;++i)
    {
        res+=dist(point[que[i]],point[que[i+1]]);
        //printf("%.2lf**\n",res);
    }
    res+=dist(point[que[1]],point[que[top]]);
    res+=2.0*PI*l;
    return res;
}
int main()
{
    while(~scanf("%d%d",&n,&l))
    {
        for(int i=1;i<=n;++i)
            scanf("%lf%lf",&point[i].x,&point[i].y);
        printf("%d\n",(int)(Graham()+0.5));
    }
    return 0;
}