[IOI1998] Polygon (区间dp,和石子合并很相似)
题意:
给你一个多边形(可以看作n个顶点,n-1条边的图),每一条边上有一个符号(+号或者*号),这个多边形有n个顶点,每一个顶点有一个值
最初你可以把一条边删除掉,这个时候这就是一个n个顶点,n-2条边的图
如果顶点i和j之间有边,那么你可以把i点和j点合并成一个点,把这个点替换掉i、j两个点,这个新点的值是i+j 或者 i*j (这个是要看连接i和j两点的边上的符号)
经过若干次操作之后剩下一个点,这个点的值最大是多少
题解:
这道题目和石子合并题目很相似,这里先说一下石子合并
题目:
有N堆石子围成一个圆,现要将石子有序的合并成一堆,规定如下:每次只能移动相邻的2堆石子合并,合并花费为新合成的一堆石子的数量。求将这N堆石子合并成一堆的总花费最小(或最大)。
我们来分析一下,给你 4 堆石子:4,5,6,7,按照下图所示合并
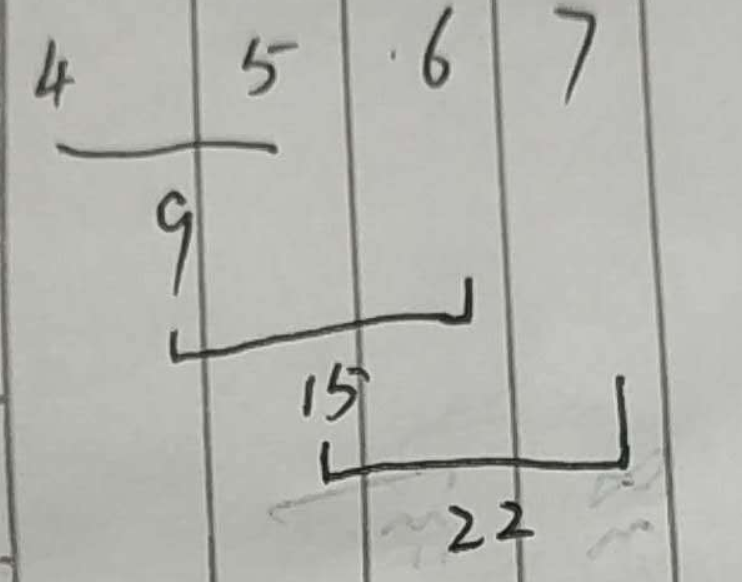
这种合并方式的花费为:4+5+9+6+15+7=46
这种合并也就是4->5->6->7按照这个方向进行
那我们先合并前3堆石子:4+5+9+6
这个花费就是:第一堆和第二堆合并的花费+第一堆和第二堆合并之后的数量+第三堆的数量
那我们先合并前4堆石子:4+5+9+6+15+7
这个花费就是:第一堆和第二堆和第三堆合并的花费(也就是4+5+9+6)+第一堆和第二堆和第三堆合并之后的数量+第四堆的数量
大问题分解成了小问题,而且大问题包含了小问题的解,大问题和小问题同质同解。完完全全满足dp的性质。
剩下的就是从中找到最优解,因为当前是从1->2->3->4的顺序去合并的,还有(1->2)->(3->4)或者1->(2->3->4)的顺序,原理一样,这里面因为第二第三部分是固定的,所以只需要得到小问题的最优解,就可以求得大问题的最优解了。这一点我们可以把原序列复制一份追加到原序列尾部,然后使用区间dp枚举就可以了
这里给出石子合并问题求最大花费的代码:dp[i][j]表示:从石子i合并到石子j所能得到的最大花费

1 #include<bits/stdc++.h> 2 using namespace std; 3 const int maxn=450;//区间长度为2*n 4 int dp[maxn][maxn]; 5 int sum[maxn];//前缀和数组 6 int a[maxn];//每堆石子的个数 7 int main() 8 { 9 int n,x; 10 sum[0]=0; 11 while(scanf("%d",&n)!=EOF){ 12 memset(dp,0,sizeof(dp)); 13 memset(sum,0,sizeof(sum)); 14 for(int i=1;i<=n;i++){ 15 scanf("%d",&a[i]); 16 sum[i]=sum[i-1]+a[i];//预处理 17 dp[i][i]=0; 18 } 19 20 int in=1;//首尾相连之后 21 for(int i=n+1;i<=2*n;i++) 22 sum[i]+=(sum[i-1]+a[in++]); 23 24 for(int len=2;len<=n;len++)//枚举区间长度 25 { 26 for(int i=1;i<=2*n;i++)//枚举区间起点 27 { 28 int j=i+len-1;//区间终点 29 if(j>n*2) break;//越界结束 30 for(int k=i;k<j;k++)//枚举分割点,构造状态转移方程 31 { 32 dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+(sum[j]-sum[i-1])); 33 } 34 } 35 } 36 int MAX=-1; 37 for(int i=1;i<=n;i++)//枚举环状序列的起点,长度为n 38 MAX=max(dp[i][i+n-1],MAX);//求最大值 39 printf("%d\n",MAX); 40 } 41 return 0; 42 }
回归原题,这个题目如果所有边的符号都是+号,那就和石子合并一样了
这里多了一个*号,那么两个很小的负数相乘也可以得到一个很大的值,这样的话,我们可以开一个三维dp,dp[i][j][k]:如果k==1,那就保存的是dp[i][j]的max
如果k==0,那就保存dp[i][j]的最小值
其他和正常区间dp一样
代码:
#include<stdio.h> #include<string.h> #include<math.h> #include<algorithm> #include<iostream> using namespace std; #define mem(a) memset(a,0,sizeof(a)) typedef long long ll; const int maxn=55; const int INF=0x3f3f3f3f; const double blo=(1.0+sqrt(5.0))/2.0; const double eps=1e-8; struct shudui { int a,b; }que[maxn]; int dp[maxn][maxn][2],num[maxn],str[maxn]; int main() { int n; while(~scanf("%d",&n)) { char s[maxn]; for(int i=1;i<=2*n;++i) { if(i%2) { scanf("%s",s); str[i/2]=s[0]; } else { scanf("%d",&num[(i-1)/2]); } } str[n]=str[0]; for(int i=0;i<n;++i) { for(int j=0;j<n;++j) { if(i==j) dp[i][j][0]=dp[i][j][1]=num[i]; else { dp[i][j][0]=INF; dp[i][j][1]=-INF; } } } for(int len=1;len<n;++len) { for(int i=0;i<n;++i) { //int j=(i+len)%n; int j=(i+len); for(int k=i;k<j;++k) { if(str[(k+1)%n]=='t') { dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][1]+dp[(k+1)%n][j%n][1]); dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]+dp[(k+1)%n][j%n][0]); } else { dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][1]*dp[(k+1)%n][j%n][1]); dp[i][j%n][1]=max(dp[i][j%n][1],dp[i][k%n][0]*dp[(k+1)%n][j%n][0]); dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]*dp[(k+1)%n][j%n][1]); dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][1]*dp[(k+1)%n][j%n][0]); dp[i][j%n][0]=min(dp[i][j%n][0],dp[i][k%n][0]*dp[(k+1)%n][j%n][0]); } } } } //printf("%d %d %d %d\n",dp[1][2][1],dp[2][1][1],dp[2][3][1],dp[3][2][1]); int maxx=-INF,index=0; for(int i=0;i<n;++i) { maxx=max(maxx,dp[i][(i+n-1)%n][1]); } for(int i=0;i<n;++i) { if(dp[i][(i+n-1)%n][1]==maxx) { //printf("%d %d\n",i,(i+n-1)%n); que[index++].a=i+1; //que[index++].b=max((i+n-1)%n,i)+1; //que[index++].a=i+1; } } printf("%d\n",maxx); for(int i=0;i<index;++i) { //printf("%d %d\n",que[i].a,que[i].b); if(i==index-1) printf("%d\n",que[i].a); else printf("%d ",que[i].a); } } return 0; }



