hdu 6827 Road To The 3rd Building

题意：

t组输入，每一组一个n，然后后面是n个树的值（我们放到数组v里面），你需要从[1,n]这个区间内挑选出来两个数i，j，你需要保证i<=j，之后你要求一下v[i]+v[i+1]+...+v[j]，然后把这个和除于j-i+1（也就是求平均值），最后答案要求的是这个平均值的期望，我们可以算出来有多少对(i，j)，我们设有sum对，然后让每一个平均值乘于1/sum，把这个都加到一起就可以了

 

题解：

sum的求法就是n*(n-1)/2

然后

 

 

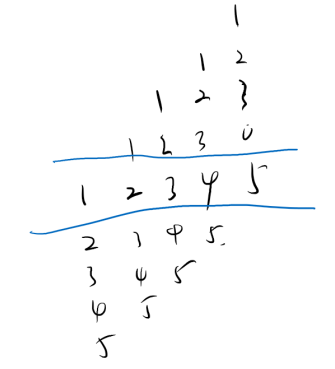
我们可以枚举区间大小，从1枚举到n，上图是区间长度为1

蓝线中间的是，区间长度为1的时候区间内的数，如果区间长度为2的时候，那么蓝线中间的就是

1234

2345

蓝线上下两侧的就是把它们都补全之后的模样，我们只需要用v的前缀和数组w，让w[n]乘于一个数然后减去上下两侧的就可以

总之就是找规律

 

 代码：

#include<stack>
#include<queue>
#include<map>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define fi first
#define se second
using namespace std;
typedef long long ll;
const int maxn=2e5+10;
const int mod=1e9+7;
ll v[maxn],p[maxn],p2[maxn],p_pre[maxn],p_suf[maxn];
ll ksc(ll a, ll b)
{
    ll ans = 0;
    while( b > 0 )
    {
        if( b&1 ) ans = (ans + a) % mod;
        a = ( a + a ) % mod;
        b >>= 1;
    }
    return ans;
}
ll ppow(ll a,ll b)
{
    ll ans=1;
    while(b)
    {
        if(b&1) ans=(ans*a)%mod;
        a=(a*a)%mod;
        b>>=1;
    }
    return ans;
}
//void init()
//{
//    ll ans = 0;
//    for (ll i = 1; i <= 6000001; i++)
//    {
//        ll x = ((i * i) % mod);
//        ans = (ans + (ppow(x, mod - 2) % mod));
//        dp[i] = (ans * 3) % mod;
//    }
//}
int main()
{

    ll t;
    scanf("%lld",&t);
    while(t--)
    {
        memset(v,0,sizeof(v));
        memset(p,0,sizeof(p));
        memset(p2,0,sizeof(p2));
        memset(p_pre,0,sizeof(p_pre));
        memset(p_suf,0,sizeof(p_suf));
        ll n,result=0,sum;
        scanf("%lld",&n);
        sum=(n*(n+1))/2;
        sum%=mod;
        for(ll i=1; i<=n; ++i)
        {
            scanf("%d",&v[i]);
            p[i]=(p[i-1]+v[i])%mod;
        }
        p2[n]=v[n];
        for(ll i=n-1; i>=1; --i)
        {
            p2[i]=(p2[i+1]+v[i])%mod;

        }
        for(ll i=1; i<=n; ++i)
        {
            p_pre[i]=(p[i]+p_pre[i-1])%mod;
        }
        p_suf[n+1]=0;
        p_suf[n]=p2[n];
        for(ll i=n-1; i>=1; --i)
        {
            p_suf[i]=(p2[i]+p_suf[i+1])%mod;
        }
        for(ll i=1; i<=n; ++i)
        {
            result = (result + (((((i*p[n])%mod)-p_pre[i - 1]-p_suf[n-i+2]+mod) % mod) * ppow(i, mod - 2)%mod))%mod;
        }
        printf("%lld\n",((result%mod)*ppow(sum,mod-2))%mod);
    }
    return 0;
}