Codeforces Round #652 (Div. 2)D. TediousLee 推导
题意:
Rooted Dead Bush (RDB) of level 1是只有一个点,如下图

当(RDB) of level i变成(RDB) of level i+1的时候,每一个顶点要进行下面的变化:
1、如果一个节点只有一个子节点,那么就再给这个节点添加两个子节点
2、如果一个节点没有子节点,那么就给这个节点添加一个子节点
3、如果一个节点有三个子节点,那么就不用管它
你需要从(RDB) of level i中找到有多少爪,爪的结构如下
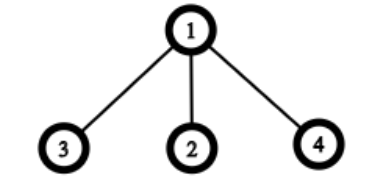
最后因为我们求的是要给多少爪的节点染色,因为一个爪有四个节点,所以最后答案就是爪的个数乘于4(注意,爪与爪之间不能有重叠节点)
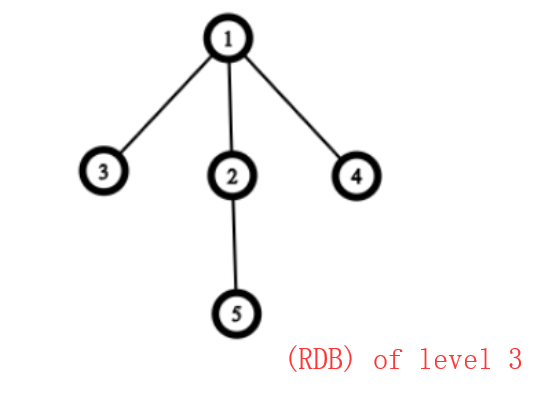
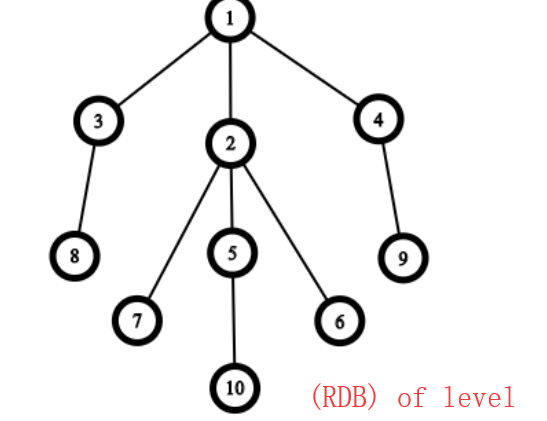
对于(RDB) of level 3只有一个爪就是(1,3,2,4);对于(RDB) of level 4种有两个爪(1,3,2,4)和(2,7,5,6)但是两个爪有重叠部分,所以只能算作一个
题解:
衍生的过程是具有重复性的,最终变化的是根结点 1 下的三棵子树,左右两棵子树为 leveln-2,中间的子树为 leveln-1 。
因为 level1 和 level2 的根结点并未使用,所以可以在 level3 中选择以根结点 1 为中心的爪形结构。
同理,level4、level5 可以通过选取较下层的爪形结构来避免根结点的使用,所以在 level6 中又可以选取以根结点 1 为中心的爪形结构。
即,level为 3 的倍数的图形都可以再额外选取位于根结点的爪形结构。
dp[i]=2*dp[i-2]+dp[i-1]+(i%3==0)*4
代码:
1 #include<iostream> 2 using namespace std; 3 #define ll long long 4 const int maxn =( 2 * 1e6)+10; 5 const int mod = 1e9 + 7; 6 ll dp[maxn], i, t, n; 7 8 void solve() 9 { 10 dp[0] = 0; 11 dp[1] = 0; 12 dp[2] = 0; 13 for (int i = 3; i <maxn; i++) 14 { 15 dp[i] = (dp[i - 1] + 2 * dp[i - 2])%mod; 16 if (i % 3 == 0) 17 { 18 dp[i] += 4; 19 dp[i] %= mod; 20 } 21 } 22 } 23 int main() 24 { 25 solve(); 26 int t; 27 cin >> t; 28 while (t--) 29 { 30 int n; 31 cin >> n; 32 cout << dp[n] << endl; 33 } 34 }


