Paths on a Grid POJ - 1942 排列组合

题意：

从左下角移动到右上角。每次只能向上或者向右移动一格。问移动的轨迹形成的右半边图形有多少种

 

题解：

注意，这个图形就根本不会重复，那就是n*m的图形，向上移动n次，向右移动m次。

 

从左下角移动到右上角的过程就是n个“上”，m个“右”的组合的形式，有多少种移动方式，那就是 C((n+m),n)或者C((n+m),m) C((n+m),n)意思就是从n+m个位置上挑选出来n个位置，这n个位置要向上走，那么剩下m个位置肯定是向右走咯

另外 无符号整型的输入输出用“%u” 无符号长整型的输入输出用“%llu”

 

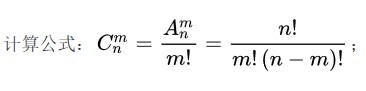
 本题的N=(n+m),M=min(n,m)

将N，M带入公式，你会发现N！与(N-M)!（N-M是max(n,m)）约分后剩下的是N*(N-1)*(N-2)*...（一共m个元素）

 

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<math.h>
#include<queue>
using namespace std;
typedef unsigned ull;
ull result(ull n,ull m) //求组合C（n，m）（n>m）
{
    ull temp;
    double ans=1.0;
    temp=min(n,m);
    n=n+m;
    m=temp;
    while(m>0)
    {
        ans=ans*((double)(n--)/(double)(m--));
    }
    ans+=0.5;
    return (ull)ans;
}
int main()
{
    unsigned m,n;
    while(true)
    {
        scanf("%u%u",&n,&m);
        if(!m && !n)//承认这题的猥琐吧！竟然有其中一边为0的矩阵，一定要&&，用||会WA
            break;
        printf("%u\n",result(n,m));
        //cout<<<<endl;
    }
    return 0;
}