Relatives POJ - 2407 欧拉函数

题意：

给你一个正整数n，问你在区间[1,n）中有多少数与n互质

 

题解：

1既不是合数也不是质数（1不是素数）

互质是公约数只有1的两个整数，叫做互质整数。公约数只有1的两个自然数，叫做互质自然数 所以1与任何整数都互质

 

 

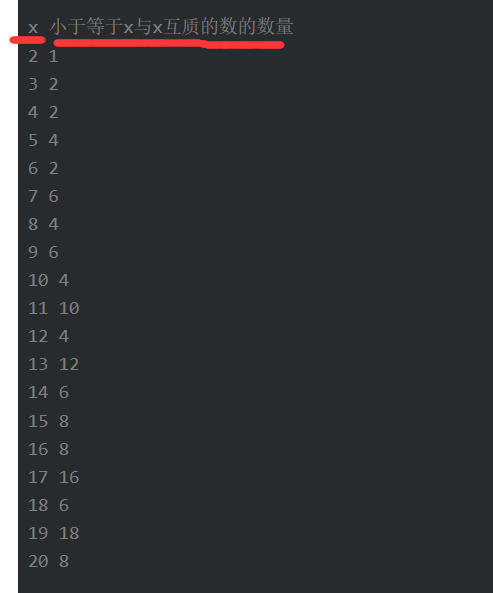
根据欧拉函数求解 欧拉函数是少于或等于n的数中与n互质的数的数目。 欧拉函数的性质：它在整数n上的值等于对n进行素因子分解后，所有的素数幂上的欧拉函数之积。 欧拉函数的值 　通式：φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn),其中p1, p2……pn为x的所有质因数，x是不为0的整数。 φ(1)=1（唯一和1互质的数(小于等 于1)就是1本身）。 (注意：每种质因数只一个。比如12=2*2*3那么φ（12）=12*（1-1/2）*(1-1/3)=4）

推论：当n为奇数时，有φ(2n)=φ(n)。

 

若n是质数p的k次幂，φ(n)=p^k-p^(k-1)=(p-1)p^(k-1)，因为除了p的倍数外，其他数都跟n互质。 设n为正整数，以 φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值，这里函数φ：N→N，n→φ(n)称为欧拉函数。 欧拉函数是积性函数——若m,n互质，φ(mn)=φ(m)φ(n)。

特殊性质：当n为奇数时，φ(2n)=φ(n), 证明与上述类似。

 

解释：

1、为什么欧拉函数是φ(x)=x(1-1/p1)(1-1/p2)(1-1/p3)(1-1/p4)…..(1-1/pn)

两个数互质是除了1不能有其他公约数 如果一个数和n互质，那么他们就没有公因数，那么我们让总数减去所有与n有公因数的数的数量就可以了 比如与n有公因数x的数的数量有多少，那不就有n/x个嘛。

所以就是这样慢慢减

2、当n为奇数时，有φ(2n)=φ(n)。

我们要求2n的互质数量，那么2n与公因数为2的数的数量由n个，所以可以说1——n这一段数都不与2n互质

 

 

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<math.h>
using namespace std;
typedef long long ll;
const int maxn=100005;
int oula(int n)
{
    int ans=n;
    for(int i=2; i<=sqrt(n); ++i)
    {
        if(n%i==0)
        {
            ans=ans-ans/i;
            n/=i;
            while(n%i==0)
                n/=i;
        }
    }
    if(n>1)
        ans=ans-ans/n;
    return ans;
}
int main()
{
    int n;
    while(~scanf("%d",&n) && n)
    {
        int result=oula(n);
        printf("%d\n",result);
    }
    return 0;
}