B - 来找一找吧 HihoCoder - 1701

题目：

这次到渣渣问桶桶了。。。

准备给你n个数a₁, a₂, ... a_n，桶桶你能从中找出m个特别的整数吗，我想让任意两个之差都是k的倍数。  

请你计算有多少种不同的选法。由于选法可能非常多，你只需要输出对1000000009取模的结果。

Input

第一行包含三个整数n、m和k。  

第二行包含n个整数a₁, a₂, ... a_n。  

对于30%的数据，2 ≤ m ≤ n ≤ 10  

对于100%的数据，2 ≤ m ≤ n ≤ 100 1 ≤ k, a_i ≤ 100

Output

一个整数表示答案。

Sample Input

5 3 2  
1 2 3 4 5

Sample Output

1

 

题解：

因为“任意两个数的差是k的倍数，那么两个数取余k后相等”,所以只需要统计一下取余k之后有多少数等于x（1<=x<k）
假设这个数是ans，然后从ans里面挑出来m个数就行（也就是排列组合）

 

 

 

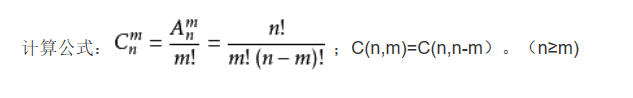
 我们这里用的第二个公式

 

但是排列组合要求阶乘，为了防止爆long long，我们要边乘边除（具体见代码）

 

 

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
#include<queue>
#include<vector>
#include<map>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=110;
const int mod=1000000009;
typedef long long ll;
ll v[maxn];
int main()
{
    ll n,m,k;
    while(~scanf("%lld%lld%lld",&n,&m,&k))
    {
        memset(v,0,sizeof(v));
        ll temp1,temp2,ans=0;
        for(ll i=0; i<n; i++)
        {
            ll x;
            scanf("%lld",&x);
            v[x%k]++;
        }
        for(ll i=0; i<k; i++)
        {
            temp1=1;
            temp2=1;
            if(v[i]<m)
                continue;
//            for(ll j=m+1; j<=v[i]; j++)
//            {
//                temp1=temp1*j;
//            }
//            for(ll j=m+1; j<=v[i]-m; j++)
//            {
//                temp2=temp2*j;
//            }
//            temp1/=temp2;
            for(ll j=m+1;j<=v[i];j++)  //这个for循环就是分子的阶乘
            {
                temp1=temp1*j;
                //注意要加判断条件temp1%temp2==0，只有这样才会保证结果正确
                while (temp1%temp2==0 && temp2<=(v[i]-m))  //这个temp2就是分母的阶乘
                {
                    temp1=temp1/temp2;
                    temp2++;
                }
            }

            ans+=(temp1%mod);
        }
        printf("%lld\n",ans);
    }
    return 0;
}