文艺平衡树算法

一、文艺平衡树解决什么问题

您需要写一种数据结构（可参考题目标题），来维护一个有序数列。

其中需要提供以下操作：翻转一个区间，例如原有序序列是 $15\ 4\ 3\ 2\ 15 4 3 2 1，翻转区间是 [2,4][2,4][2,4] 的话，结果是 5 2 3 4 15\ 2\ 3\ 4\ 15 2 3 4 1。$

$二、文艺平衡树与平衡树$

$a[5]={5,4,3,1,2};那么存入文艺平衡树后，再中序遍历的结果应该还是：{5，4，3，1，2}。即下标从小到大，而不是里面的值从小到大！这是与SBT树(平衡树)最大的不同！文艺平衡树经过rotates旋转后，它的中序遍历结果是不变的（即，下标从小到大）但是让这棵树的一部分区间倒置之后。这个中序遍历下标就不是递增的了（所以它不是平衡树）$

平衡树算法

$三、文艺平衡树构造$

1、建树

就像线段树建树一样，但是在原数据的基础上加上一个-INF，+INF。(比如原序列是1，2，3，4.你建树的时候要给-INF，1，2，3，4，+INF建树)

至于为什么要这样做，就是为了可以给区间[1,n]倒置

主函数：

 1 int main()
 2 {
 3     scanf("%d%d",&n,&m);
 4     for (int i=1; i<=n; i++) data[i+1]=i;
 5     data[1]=-INF;
 6     data[n+2]=INF;
 7     rt=build_tree(0,1,n+2);
 8     for (int i=1; i<=m; i++)
 9     { //m是要翻转多少次区间
10         scanf("%d%d",&x,&y);
11         turn(x,y);
12     }
13     write(rt);
14     return 0;
15 }

这个没有输入对应的n个数，而是用1，2......n来代表，你也可以输入

 1 bool get(int x)  //得到x是右孩子还是左孩子
 2 {
 3     return ch[f[x]][1]==x;
 4 }
 5 void pushup(int x)  //更新节点的信息
 6 {
 7     sizes[x]=sizes[ch[x][0]]+sizes[ch[x][1]]+1;
 8 //这个是文艺平衡树
 9     /*
10     a[5]={5,4,3,1,2};那么存入伸展树后，再中序遍历的结果应该还是：{5，4，3，1，2}。
11     即下标从小到大，而不是里面的值从小到大！这是与SBT树(平衡树)最大的不同！
12     文艺平衡树经过rotates旋转后，它的中序遍历结果是不变的
13     但是让这棵树的一部分区间倒置之后。这个中序遍历结果就不是递增的了（所以它不是平衡树）
14     */
15 }
16 void pushdown(int x)  //相当于线段树操作的懒惰标记
17 {
18     if(x && tag[x])
19     {
20 //这个tag标记就是用来看这个子树用不用交换（他的交换也就对应着区间的翻转）
21         tag[ch[x][0]]^=1;
22         tag[ch[x][1]]^=1;
23         swap(ch[x][0],ch[x][1]);
24         tag[x]=0;
25     }
26 }

 1 int build_tree(int fx,int l,int r)
 2 {
 3     //用所给数组data中数据建一棵树(就是普通线段树建树)
 4     if(l>r) return 0;
 5     int mid=(l+r)>>1;
 6     int now=++sz;
 7     key[now]=data[mid];
 8     f[now]=fx;
 9     tag[now]=0;
10 
11     ch[now][0]=build_tree(now,l,mid-1);
12     ch[now][1]=build_tree(now,mid+1,r);
13     pushup(now);
14     return now;
15 }

先序遍历输出

void write(int now)
{
    //按照中序遍历输出序列
    pushdown(now);
    if(ch[now][0]) write(ch[now][0]);
    if(key[now]!=-INF && key[now]!=INF) printf("%d ",key[now]);
    if(key[ch[now][1]]) write(ch[now][1]);
}

。

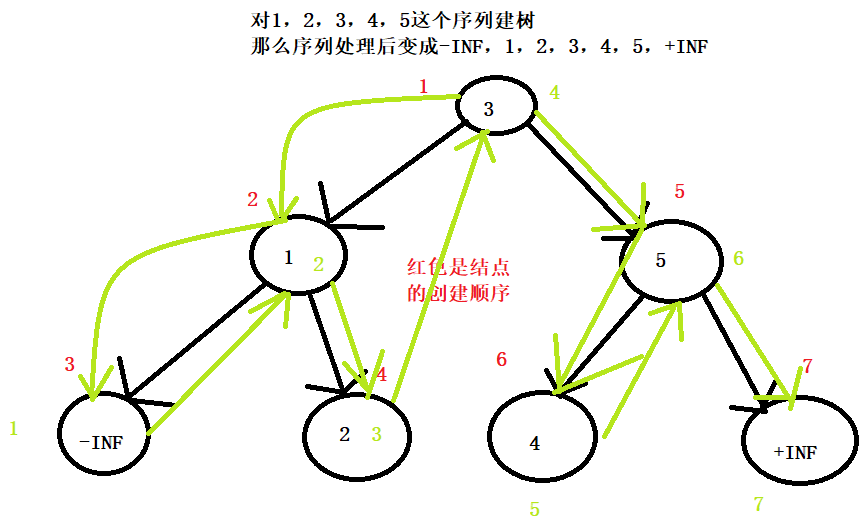绿色的线就是输出的过程，绿色的数字就是输出顺序

2、区间翻转操作

参考链接：https://blog.csdn.net/a_comme_amour/article/details/79382104

旋转操作和平衡树旋转一样（这里就不重复讲了，可以看一下平衡树算法）

就是x旋转到他父亲节点的位置

void rotates(int x) //这个也就是平衡树的旋转，这样旋转后的话是不影响中序遍历结果的
{
    int fx=f[x];
    int ffx=f[fx];
    int which=get(x);
    pushdown(fx);
    pushdown(x);
    ch[fx][which]=ch[x][which^1];
    f[ch[fx][which]]=fx;

    ch[x][which^1]=fx;
    f[fx]=x;

    f[x]=ffx;
    if(ffx) ch[ffx][ch[ffx][1]==fx]=x;
    pushup(fx);
    pushup(x);
}

Splay操作，就是加了一个目的地，让x旋转到goal这个位置

void splay(int x,int goal)  //这个就是提供了一个旋转的终点，将树上面x的点转移到树上goal这个位置
{
    for(int fx; (fx=f[x])!=goal; rotates(x))
    {
        if(f[fx]!=goal)
            rotates((get(x)==get(fx))?fx:x);
    }
    if(!goal) rt=x;
}

若要翻转[l+1, r+1]，将r+2 Splay到根，将l Splay到 r+2 的左儿子，然后[l+1, r+1]就在根节点的右子树的左子树位置了，给它打上标记

《1》、先使l旋转到根

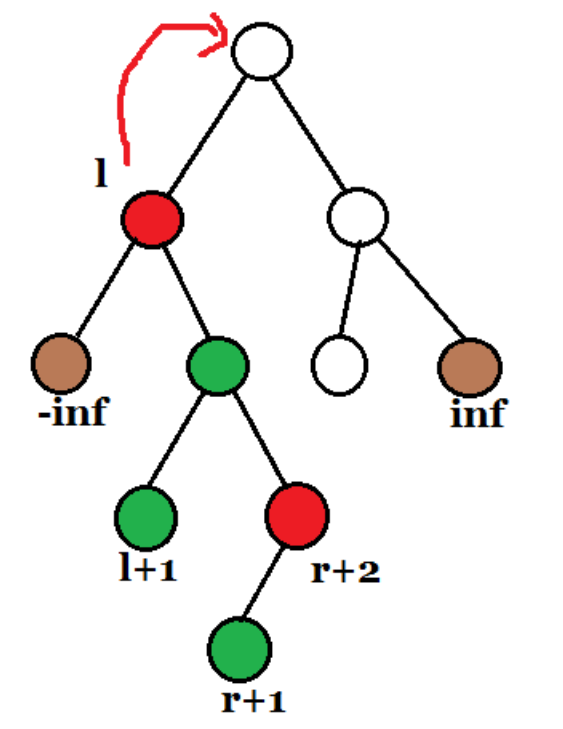
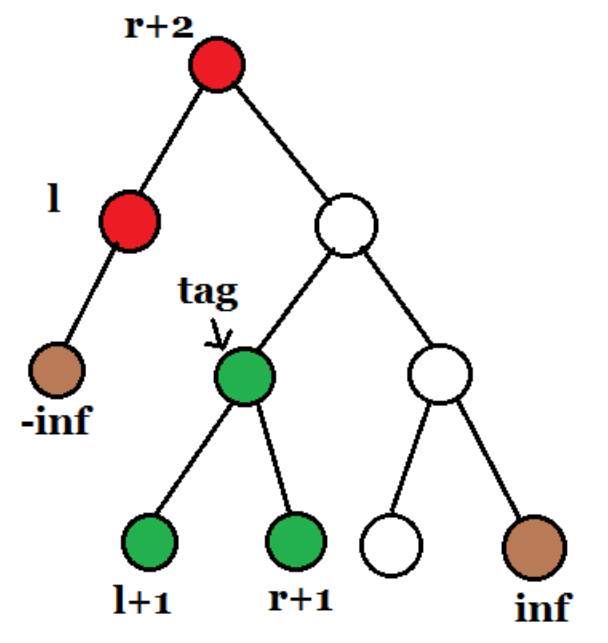
《2》、使r+2旋转到根

由于l < r+2,此时l成了r+2的左子树，那么r+2的右子树的左子树即为所求得区间，我们就可以对这棵子树随意操作了！比如删除整个区间，区间内的每个数都加上x，区间翻转，区间旋转等。

四、例题

P3391 【模板】文艺平衡树

题目描述

您需要写一种数据结构（可参考题目标题），来维护一个有序数列。

其中需要提供以下操作：翻转一个区间，例如原有序序列是 $15\ 4\ 3\ 2\ 15 4 3 2 1，翻转区间是 [2,4][2,4][2,4] 的话，结果是 5 2 3 4 15\ 2\ 3\ 4\ 15 2 3 4 1。$

输入格式

第一行两个正整数

输出格式

输出一行

输入输出样例

输入 #1

输出 #1

4 3 2 1 5

说明/提示

【数据范围】
对于 $100%100\%100% 的数据，1≤n,m≤1000001 \le n, m \leq 100000 1≤n,m≤100000，1≤l≤r≤n1 \le l \le r \le n1≤l≤r≤n。$

代码：

  1 #include<stdio.h>
  2 #include<string.h>
  3 #include<algorithm>
  4 #include<iostream>
  5 using namespace std;
  6 const int maxn=1e5+10;
  7 const int INF=1e9;
  8 int f[maxn],cnt[maxn],ch[maxn][2],sizes[maxn],key[maxn],tag[maxn],sz,rt;
  9 int n,m,x,y,data[maxn];
 10 bool get(int x)
 11 {
 12     return ch[f[x]][1]==x;
 13 }
 14 void pushup(int x)
 15 {
 16     sizes[x]=sizes[ch[x][0]]+sizes[ch[x][1]]+1;
 17 //这个是文艺平衡树
 18     /*
 19     a[5]={5,4,3,1,2};那么存入伸展树后，再中序遍历的结果应该还是：{5，4，3，1，2}。
 20     即下标从小到大，而不是里面的值从小到大！这是与SBT树(平衡树)最大的不同！
 21     文艺平衡树经过rotates旋转后，它的中序遍历结果是不变的
 22     但是让这棵树的一部分区间倒置之后。这个中序遍历结果就不是递增的了（所以它不是平衡树）
 23     */
 24 }
 25 void pushdown(int x)
 26 {
 27     if(x && tag[x])
 28     {
 29 //这个tag标记就是用来看这个子树用不用交换（他的交换也就对应着区间的翻转）
 30         tag[ch[x][0]]^=1;
 31         tag[ch[x][1]]^=1;
 32         swap(ch[x][0],ch[x][1]);
 33         tag[x]=0;
 34     }
 35 }
 36 void rotates(int x) //这个也就是平衡树的旋转，这样旋转后的话是不影响中序遍历结果的
 37 {
 38     int fx=f[x];
 39     int ffx=f[fx];
 40     int which=get(x);
 41     pushdown(fx);
 42     pushdown(x);
 43     ch[fx][which]=ch[x][which^1];
 44     f[ch[fx][which]]=fx;
 45 
 46     ch[x][which^1]=fx;
 47     f[fx]=x;
 48 
 49     f[x]=ffx;
 50     if(ffx) ch[ffx][ch[ffx][1]==fx]=x;
 51     pushup(fx);
 52     pushup(x);
 53 }
 54 void splay(int x,int goal)  //这个就是提供了一个旋转的终点，将树上面x的点转移到树上goal这个位置
 55 {
 56     for(int fx; (fx=f[x])!=goal; rotates(x))
 57     {
 58         if(f[fx]!=goal)
 59             rotates((get(x)==get(fx))?fx:x);
 60     }
 61     if(!goal) rt=x;
 62 }
 63 int build_tree(int fx,int l,int r)
 64 {
 65     //用所给数组data中数据建一棵树(就是普通线段树建树)
 66     if(l>r) return 0;
 67     int mid=(l+r)>>1;
 68     int now=++sz;
 69     key[now]=data[mid];
 70     f[now]=fx;
 71     tag[now]=0;
 72 
 73     ch[now][0]=build_tree(now,l,mid-1);
 74     ch[now][1]=build_tree(now,mid+1,r);
 75     pushup(now);
 76     return now;
 77 }
 78 int kth(int x)  //这个就是获取原输入数组中第x个元素在树上的位置
 79 {
 80     int now=rt;
 81     while(1)
 82     {
 83         pushdown(now);
 84         if(x<=sizes[ch[now][0]]) now=ch[now][0];
 85         else
 86         {
 87             x-=sizes[ch[now][0]]+1;
 88             if(!x) return now;
 89             now=ch[now][1];
 90         }
 91     }
 92 }
 93 void turn(int l,int r) //将区间[l,r]翻转
 94 {
 95     l=kth(l);
 96     r=kth(r+2);
 97     splay(l,0);
 98     splay(r,l);
 99     pushdown(rt);
100     tag[ch[ch[rt][1]][0]]^=1; //根的右子树的左子树
101 }
102 void write(int now)
103 {
104     //按照中序遍历输出序列
105     pushdown(now);
106     if(ch[now][0]) write(ch[now][0]);
107     if(key[now]!=-INF && key[now]!=INF) printf("%d ",key[now]);
108     if(key[ch[now][1]]) write(ch[now][1]);
109 }
110 int main()
111 {
112     scanf("%d%d",&n,&m);
113     for (int i=1; i<=n; i++) data[i+1]=i;
114     data[1]=-INF;
115     data[n+2]=INF;
116     rt=build_tree(0,1,n+2);
117     for (int i=1; i<=m; i++)
118     {
119         scanf("%d%d",&x,&y);
120         turn(x,y);
121     }
122     write(rt);
123     return 0;
124 }

posted @ 2020-01-20 15:51 kongbursi 阅读(2147) 评论(0) 编辑收藏举报

刷新页面返回顶部

哟吼！