五种排序算法整理 二(堆排序,快速排序、插入排序、选择排序、冒泡排序)
一、快速排序算法步骤:(从小到大排序)
1. 在数组中选一个基准数(通常为数组第一个);
2. 将数组中小于基准数的数据移到基准数左边,大于基准数的移到右边;
3. 对于基准数左、右两边的数组,不断重复以上两个过程,直到每个子集只有一个元素,即为全部有序。
实例演示
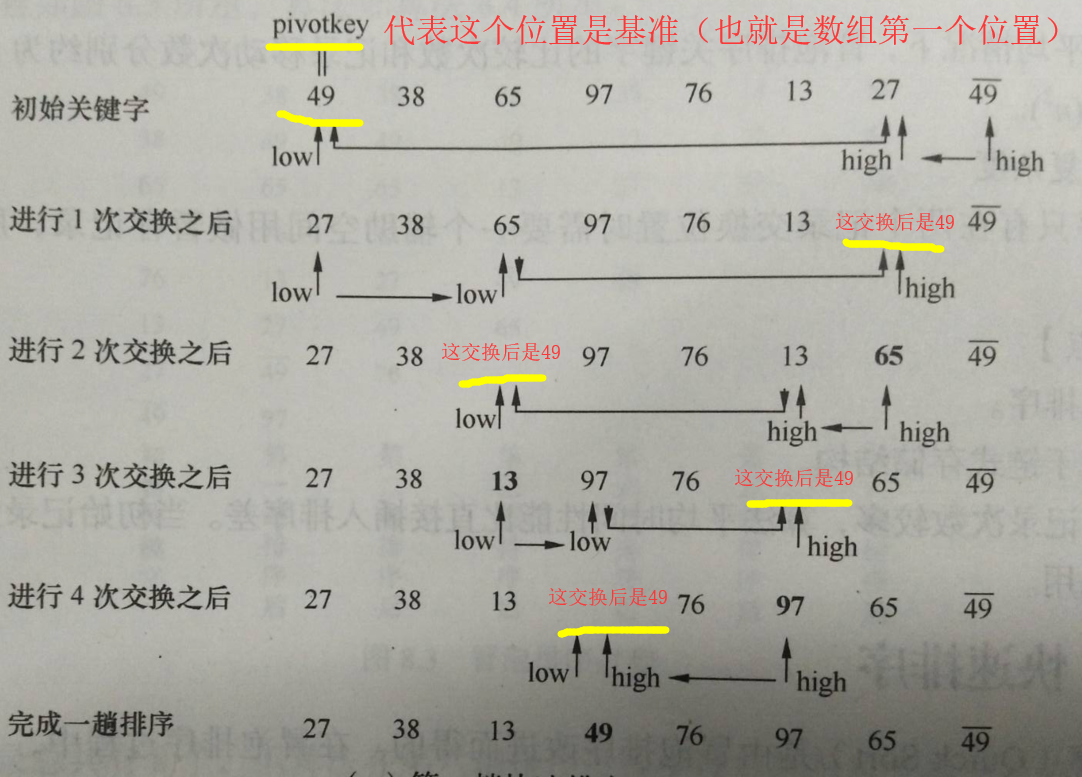

这个算法就是先找一个基准,对着一个[l,r]区间按照基准排过序后(也不算排序,就是大于基准的放右边,小于基准的放左边)。这个时候假设基准在数组中下标为x。这个时候在对[l,x)和(x,r]则两个区间在进行一次这样的排序。一直进行到区间内部只剩下一个元素就截至
这个时候数组内元素已经排好序了
代码:

1 #include <string.h> 2 #include <stdio.h> 3 #include <algorithm> 4 #include <iostream> 5 using namespace std; 6 const int N = 7; 7 const int MAX = 0x3f3f3f3f; 8 int root[N+1][N+1]; 9 double e[N+2][N+1],w[N+2][N+1]; 10 double p[N + 1] = { 0.04 ,0.06, 0.08, 0.02, 0.10, 0.12, 0.14 }; 11 double q[N + 1] = { 0.06 ,0.06, 0.06, 0.06, 0.05, 0.05, 0.05, 0.05 }; 12 void bst_search_tree() 13 { 14 memset(w, 0, sizeof(w)); 15 for (int i = 1; i <= N+1; ++i) 16 { 17 root[i][i] = i; 18 e[i][i - 1] = w[i][i - 1] = q[i - 1]; 19 } 20 for (int len = 1; len <= N; ++len) 21 { 22 for (int i = 1; i <= N - len + 1; ++i) 23 { 24 int j = i + len - 1; 25 w[i][j] = w[i][j - 1] + p[j] + q[j]; 26 e[i][j] = MAX; 27 for (int r = i; r <= j; ++r) 28 { 29 double tmp = e[i][r - 1] + e[r + 1][j] + w[i][j]; 30 if (tmp < e[i][j]) 31 { 32 e[i][j] = tmp; 33 root[i][j] = r; 34 } 35 } 36 } 37 } 38 } 39 void print(int s,int e) 40 { 41 if (!(root[s][e] >= s && root[s][e] <= e)) return; 42 if (s == 1 && e == N) 43 { 44 cout << "tree root" << " " << root[s][e] << endl; 45 } 46 if (root[s][e] != s) { 47 cout << root[s][e] << " left root " << root[s][root[s][e]-1] << endl; 48 } 49 if (root[s][e] != e) { 50 cout << root[s][e] << " right root " << root[root[s][e] + 1][e] << endl; 51 } 52 print(root[s][e] + 1, e); 53 //printf("----------"); 54 print(s, root[s][e] - 1); 55 56 57 } 58 const int NN = 1005; 59 int sort_c[NN] = { 3,5,1,2,4 }; 60 void sort_s(int s, int e) 61 { 62 if (s >= e) return; 63 int l = s, r = e, m = sort_c[s]; 64 while (l < r) 65 { 66 while (m < sort_c[r] && l < r) 67 { 68 r--; 69 } 70 if (l<r) { 71 sort_c[l++] = sort_c[r]; 72 } 73 while (m > sort_c[l] && l < r) 74 { 75 l++; 76 } 77 if (l<r) { 78 sort_c[r--] = sort_c[l]; 79 } 80 } 81 sort_c[l] = m; 82 sort_s(s, m-1); 83 sort_s(m + 1, e); 84 } 85 86 int main() 87 { 88 /*最优二叉查找树测试 89 bst_search_tree(); 90 print(1, N);*/ 91 int n; 92 cin >> n; 93 for (int i = 0; i < n; ++i) { 94 cin >> sort_c[i]; 95 } 96 sort_s(0, n-1); 97 for (int i = 0; i < n; ++i) { 98 printf("%d ", sort_c[i]); 99 } 100 system("pause"); 101 return 0; 102 } 103 /* 104 6 105 4 2 1 7 2 1 106 */
二、插入排序
思路:(以从小到大排序做例子)
从第二个元素开始,将当前元素插入到前面对应位置,使当前元素i和之前元素形成有序数组。(数组保存元素[0......(n-1)])
比较规则:
使得第i个元素和前面已经有序的[0......(i-1)]倒着进行比较(到这就是先和第i-1位元素比较,再比较i-2位元素......依次进行,我们设保存i-1,i-2这些位置的变量为j)
1、如果v[i]<v[j],v[j+1]=v[j],j--。然后再判断直到j==0
2、否则跳出循环,v[j+1]=v[i]

三、选择排序
从数组中找到最小的元素,和第一个位置的元素互换。
从第二个位置开始,找到最小的元素,和第二个位置的元素互换。
........
直到选出array.length-1个较小元素,剩下的最大的元素自动排在最后一位。
四、冒泡排序
1.原理:比较两个相邻的元素,将值大的元素交换到右边
2.思路:依次比较相邻的两个数,将比较小的数放在前面,比较大的数放在后面。
(1)第一次比较:首先比较第一和第二个数,将小数放在前面,将大数放在后面。
(2)比较第2和第3个数,将小数 放在前面,大数放在后面。
......
(3)如此继续,知道比较到最后的两个数,将小数放在前面,大数放在后面,重复步骤,直至全部排序完成
(4)在上面一趟比较完成后,最后一个数一定是数组中最大的一个数,所以在比较第二趟的时候,最后一个数是不参加比较的。
(5)在第二趟比较完成后,倒数第二个数也一定是数组中倒数第二大数,所以在第三趟的比较中,最后两个数是不参与比较的。
(6)依次类推,每一趟比较次数减少依次
全部排序算法代码见上一篇博客:



