动态主席树【带修改】&& 例题 Dynamic Rankings ZOJ - 2112

参考链接：https://blog.csdn.net/WilliamSun0122/article/details/77885781

一、动态主席树介绍

动态主席树与静态主席树的不同在于：静态主席树不能支持后期对区间内数的修改。

例如：刚开始区间内的数为1、4、3、2、5.你再建完主席树之后要把第二个位置的4改成2。这在原来的静态主席树上是没法操作的。只有重新在建一棵静态主席树

但是动态主席树可以借助树状数组和主席树 【权值线段树】来支持修改操作（也就是树套树了）

 

建议没有学过树状数组和主席树 【权值线段树】可以先学习一下

 

二、动态主席树构造

动态主席树与静态主席树在代码上的区别就在于，我们用树状数组又维护了一批权值线段树。用树状数组维护的权值线段树和静态主席树维护的权值线段树一起保证着每一个区间对应权值的正确性

 

以例题：Dynamic Rankings ZOJ - 2112的样例来解释一下

5 3
3 2 1 4 7
Q 1 4 3 询问区间[1,4]第3小数
C 2 6 把第2个数变为6
Q 2 5 3 询问区间[2,5]第3小数

 

介绍一下代码中各变量作用：

//n是原序列个数 ，q是询问次数
//T[i]表示第i棵线段树的根节点编号
//S[i]表示树状数组思维建的第i棵线段树的根节点编号
//L[i]表示节点i的左子节点编号
//R[i]表示节点i的右子节点编号
//sum[i]表示节点i对应区间中数的个数。
//origin[i]存放输入的n个数据
//v[i]存放输入的n个数据，以及后面要修改后的数据的值。要对他们进行排序、去重操作。
//这个ur、ul是在查询函数query中和静态查询连在一起用的，这个具体看代码，比较难解释。
 
注意：
这里离散化建树过程和静态主席树有一点不同，我们必须把所有询问先存起来并且把改变的数也加入到原序列中再离散化建树
如上例：v[]数组里面的数应该是3、2、1、4、7、6
我们离散化后序列为3 2 1 4 6 5分别对应原序列的3 2 1 4 7和  改变后的6。
 
然后按照正常方法建立一颗静态主席树：

 

 

 

 

 

 

 

 

 

 

 

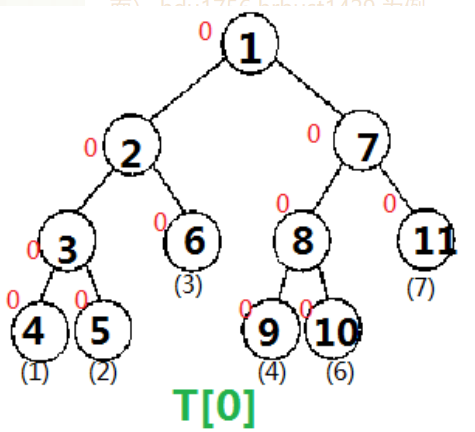
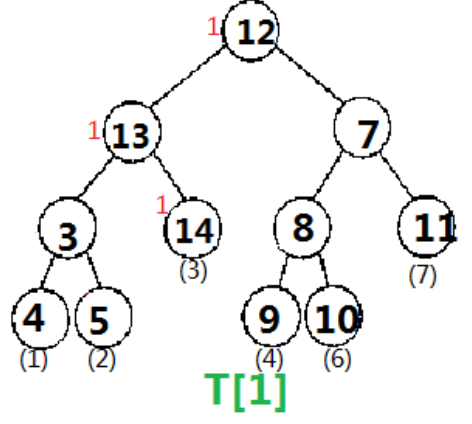
为了保证我们可以进行修改操作，我们新建一批权值线段树来记录更新，这些线段树以树状数组的思维来维护。
一开始，S[0]、S[1]、S[2]、S[3]、S[4]、S[5] （注意一共有n+1个 即 0到n）(树状数组的每个节点)这些都与T[0]相同(也就是每个节点建了一棵空树)。
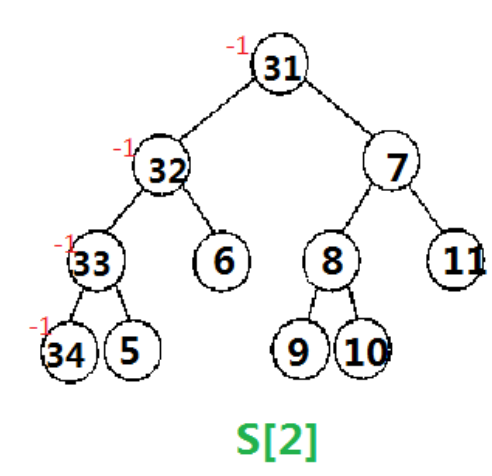
对于C 2 6 这个操作， 我们只需要减去一个2，加上一个5（为什么是5？因为我们是对权值线段树处理，那么我们要在树状数组维护的权值线段树加上6，就要加上离散化之后的值。减去那个2也是这个意思）。

 

这个更新我们按树状数组的思想更新，比如这里的减2，我们要从i=2（原序列中第2个数2在离散化后序列中的位置）即S[2]开始更新，并往上lowbit(i)直到大于5，这里我们会更新S[2]和S[4]（因为在树状数组中S[2]和S[4]包含离散化之后的2）。

减2例图：

 

 

 

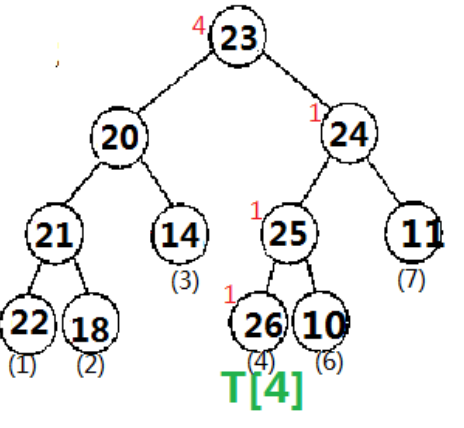
加5例图（因为加5操作是把2位置更新成6，所以树状数组还是要修改S[2],S[4]两棵树）：

 

 

 

 

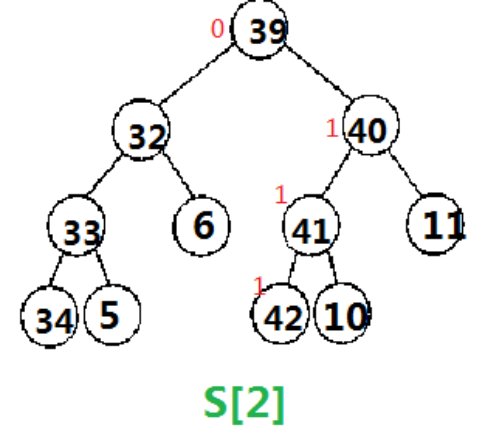
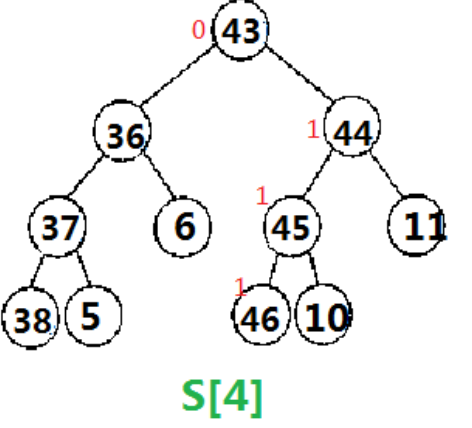
 这里我们的更新操作只会对树状数组维护的权值线段树进行操作，对于那个静态权值线段树我们并不进行修改

这个样子在我们查询某个区间中的权值大小时，我们既要考虑静态线段树的区间对应权值，还要考虑树状数组维护的区间对应权值

怎么找？

对于静态主席树的我就不用说了，还按原来的方法

对于树状数组维护的权值线段树，要找区间[l,r]权值，我们可以找到[1,l-1]和[1,r]的权值，这个找法和树状数组正常找法一样。让[1,r]的权值减去[1,l-1]的权值就可以了

 

3、复杂度

n是原序列长度，q是q次询问

时间复杂度为单次lognlogn 共nlogn+qlognlogn 或者不用前缀和 (n+q)lognlogn 空间复杂度为 qlognlogn 或者不用前缀和 (q+n)logn*logn 用垃圾回收重复利用空间可以 去掉一个logn的空间 nlogn 因为树状数组没有必要在修改之后再用修改之前的总共就只要开nlogn的空间因为c数组n个就可以了每个一条顶到叶子的链logn的空间，可以直接使用或者回收利用

4、例题代码

  1 /*动态主席树（带修改的主席树），求区间内第k大*/
  2 #include<stdio.h>
  3 #include<string.h>
  4 #include<iostream>
  5 #include<algorithm>
  6 using namespace std;
  7 const int maxn=6e4+10;  //数组开小也会segmentation fault
  8 const int maxm=1e4+10;  //我之前开的5e4+10
  9 int T[maxn],S[maxn],L[maxn*32],R[maxn*32],sum[maxn*32];
 10 int origin[maxn],v[maxn];
 11 int ul[maxn],ur[maxn];
 12 int cnt,n,q,num;
 13 //n是原序列个数 ，q是询问次数
 14 //T[i]表示第i棵线段树的根节点编号
 15 //S[i]表示树状数组思维建的第i棵线段树的根节点编号
 16 //L[i]表示节点i的左子节点编号
 17 //R[i]表示节点i的右子节点编号
 18 //sum[i]表示节点i对应区间中数的个数。
 19 //origin[i]存放输入的n个数据
 20 //v[i]存放输入的n个数据，以及后面要修改后的数据的值。要对他们进行排序、去重操作。
 21 
 22 //这个ur、ul是在查询函数query中和静态查询连在一起用的
 23 
 24 struct Node  //存放的是q次的询问，因为我们带修改的主席树也是要在v里面统计修改后的数据的值
 25 {
 26     int l,r,k;
 27     bool flag;
 28 }Q[maxm];
 29 void build(int& rt,int l,int r) //就是普通的给一个区间建立一个线段树
 30 {
 31     rt=++cnt;
 32     sum[rt]=0;
 33     if(l==r) return;
 34     int mid=(l+r)>>1;
 35     build(L[rt],l,mid); //注意这里是小写的L，可不是1
 36     //把它换成1结果对，但是交上去会出错segmentation fault
 37     build(R[rt],mid+1,r);
 38 }
 39 void update(int &rt,int pre,int l,int r,int x,int val)  //更新某一棵树上的某个位置的权值
 40 {
 41     rt=++cnt;
 42     L[rt]=L[pre];
 43     R[rt]=R[pre];
 44     sum[rt]=sum[pre]+val;
 45     if(l==r) return;
 46     int mid=(l+r)>>1;
 47     if(x<=mid) update(L[rt],L[pre],l,mid,x,val);
 48     else update(R[rt],R[pre],mid+1,r,x,val);
 49 }
 50 int lowbit(int x)
 51 {
 52     return x&(-x);
 53 }
 54 void add(int x,int val)
 55 {
 56     int ans=lower_bound(v+1,v+num+1,origin[x])-v;
 57     while(x<=n)
 58     {
 59         update(S[x],S[x],1,num,ans,val);
 60         x+=lowbit(x);
 61     }
 62 }
 63 int Sum(int x,int flag)  //它求的是1-x这所有权值线段树某个区间权值之和
 64 {
 65     int ans=0;
 66     while(x>0)
 67     {
 68         if(flag) ans+=sum[L[ur[x]]];
 69         else ans+=sum[L[ul[x]]];
 70         x-=lowbit(x);
 71     }
 72     return ans;
 73 }
 74 int query(int s,int e,int ts,int te,int l,int r,int k)
 75 {
 76     if(l==r) return l;
 77     int mid=(l+r)>>1;
 78     //因为我们用树状数组来维护的，所以在求对应静态数组的那个ans的时候，我们还要考虑一下树状数组维护的线段树的权值
 79     int ans=Sum(e,1)-Sum(s,0)+sum[L[te]]-sum[L[ts]];
 80     if(k<=ans)
 81     {
 82         for(int i=e;i;i-=lowbit(i)) ur[i]=L[ur[i]];  //因为区间是逐渐缩小的，所有我们对应
 83         for(int i=s;i;i-=lowbit(i)) ul[i]=L[ul[i]];
 84         return query(s,e,L[ts],L[te],l,mid,k);
 85     }
 86     else
 87     {
 88         for(int i=e;i;i-=lowbit(i)) ur[i]=R[ur[i]];
 89         for(int i=s;i;i-=lowbit(i)) ul[i]=R[ul[i]];
 90         return query(s,e,R[ts],R[te],mid+1,r,k-ans);
 91     }
 92 }
 93 int main()
 94 {
 95     int t,m;
 96     scanf("%d",&t);
 97     while(t--)
 98     {
 99         char str[10];
100         num=0;
101         scanf("%d%d",&n,&q);
102         num=n;
103         for(int i=1;i<=n;++i)
104             scanf("%d",&origin[i]),v[i]=origin[i];
105         for(int i=1;i<=q;++i)
106         {
107             scanf("%s",str);
108             if(str[0]=='Q')
109             {
110                 scanf("%d%d%d",&Q[i].l,&Q[i].r,&Q[i].k);
111                 Q[i].flag=1;
112             }
113             else
114             {
115                 scanf("%d%d",&Q[i].l,&Q[i].r);
116                 v[++num]=Q[i].r;
117                 Q[i].flag=0;
118             }
119         }
120         sort(v+1,v+1+num);
121         num=unique(v+1,v+1+num)-v-1;
122         printf("%d****\n",num);
123         cnt=0;
124         build(T[0],1,num);
125         for(int i=1;i<=n;++i)
126             update(T[i],T[i-1],1,num,lower_bound(v+1,v+1+num,origin[i])-v,1);
127         for(int i=1;i<=n;++i)
128             S[i]=T[0];
129         for(int i=1;i<=q;++i)
130         {
131             if(Q[i].flag)
132             {
133                 for(int j=Q[i].r;j;j-=lowbit(j)) ur[j] = S[j];
134                 for(int j=Q[i].l-1;j;j-=lowbit(j)) ul[j] = S[j];
135                 printf("%d\n",v[query(Q[i].l-1,Q[i].r,T[Q[i].l-1],T[Q[i].r],1,num,Q[i].k)]);
136 
137             }
138             else
139             {
140                 add(Q[i].l,-1);
141                 origin[Q[i].l]=Q[i].r;
142                 add(Q[i].l,1);
143             }
144         }
145     }
146     return 0;
147 }

 

 

 

 

 

posted @ 2019-12-18 16:12  kongbursi  阅读(253)  评论(0)  编辑  收藏  举报