主席树 【权值线段树】 && 例题K-th Number POJ - 2104
一、主席树与权值线段树区别
主席树是由许多权值线段树构成,单独的权值线段树只能解决寻找整个区间第k大/小值问题(什么叫整个区间,比如你对区间[1,8]建立一颗对应权值线段树,那么你不能询问区间[2,5]第k大/小值,你只能询问[1,8]第k大/小值问题)
二、权值线段树是什么鬼
学权值线段树之前你肯定要知道线段树,线段树是对区间中的所有数进行维护
权值线段树维护的对象和它不同,权值<==>这个数在这个区间中出现的次数
例如1、5、3、2、4
建立的权值线段树:
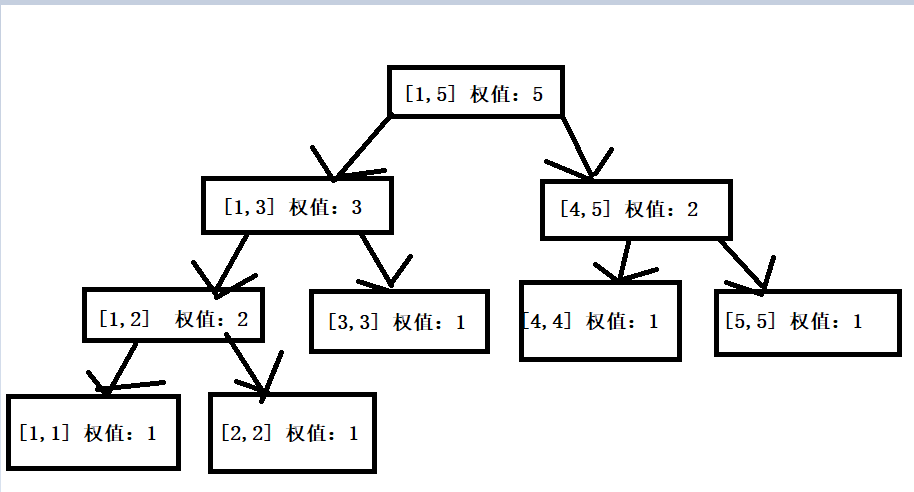
你会发现,权值线段树的建立和线段树不一样,线段树要考虑每一个数在区间中的位置
但是权值线段树不用管,相当于排完序之后建立的一颗树 。 要注意:权值代表这个数出现了几次
例如:我们寻找这个区间的第3小值
我们从根节点[1,5]的左节点来判断,因为左节点的权值要大于3,所以区间内第3小值肯定在根节点的左区间内
我们再看区间[1,3]的左节点,发现它的左节点权值为2小于3,所以答案肯定在区间[1,3]的右节点内。注意:这个时候我们要在右节点内寻找第3-2小值
之后那区间[3,3]内第1小值肯定就是3本身了
要注意如果题目给你的数据特别大,例如1、1000、200000000这三个数,我们要是直接建立权值线段树,那内存就炸了
所以这个时候就要离散化处理
三、主席树构成
我们文章开头说过,主席树是由许多权值线段树构成,而且主席树可以解决:在对应区间建立的主席树,可以找寻该区间所有子区间内的第k大/小值
(即、对区间[1,5]建立主席树,那么我们也可以找寻区间[1,3]的第k大/小值)
1、解决方法1:
排序后找到那个位置输出(不用想了,暴力方法肯定会被卡)
2、解决方法2:
对于一个区间[l, r]我们用一个用这个区间内出现过的数的个数组成一颗权值线段树,然后查询就完事了
但是多次询问区间第k小,我们每次这样建立一个线段树,这样不仅空间复杂度非常之高,而且时间复杂度也非常高,甚至比普通排序还要高,那么我们只不是可以想一个办法,使得对于每次我们查询不同的区间我们不需要重新建树,如果这样。时间复杂度和空间复杂度就大大降低了。
3、解决方法3:
这就用到了前缀和,比如我们有一个问题。就是每次静态的求区间和,我们可以预处理所以的前缀和sum[i],我们每次求解区间[l, r]和时,我们可以直接得到答案为sum[r] - sum[l -1],这样就不需要对区间中的每个数进行相加来求解了。(这里我们设sum[i]中放的是权值线段树上i节点的权值)
想到就写起来
我们可以对区间[1,5]建立6棵权值线段树,分别是[0,0],[1,1],[1,2],[1,3],[1,4],[1,5] ([0,0]是一颗空树)
这样我们处理任意区间[l, r]时就可以通过处理区间[1,l - 1], [1,r],就行,然后两者的处理结果进行相加相减就行。为什么满足相加减的性质,我们简单分析一下就很容易得出。如果在区间[1,l - 1]中有x个数小于一个数,在[1,r]中有y个数小于那个数,那么在区间[l,r]中就有y - x 个数小于那个数了,这样就很好理解为什么可以相加减了,另外,每颗树的结构都一样,都是一颗叶节点为n个的线段树。
上述利用前缀和的思想只是解决了时间复杂度的问题,并没有解决空间复杂度的问题,要解决空间复杂度问题。我们需要用到线段树的性质,我们每次更新一个数,那么与更新之前相比,这颗线段树改变只是一条链(从根节点到某一叶节点),那么我们可以充分利用这个特点,因为第i颗树与第i- 1颗树相比,只是更新了第i个元素,那么实际上第i颗树与第i-1颗树之间只有log个节点的信息是不同的。.所以这两棵树有很多相同的节点,所以这两棵树可以共用很多节点,也就是说,我们在第i-1颗树上 插入一个节点a[i] 得到第i颗权值线段树,而单点插入过程中只会修改根到那个叶子节点的路径上的那log个节点。于是这样就解决空间复杂度问题。
还是以上面的1、3、2、5、4为例子:
1、刚开始的空树

2、加一个1节点
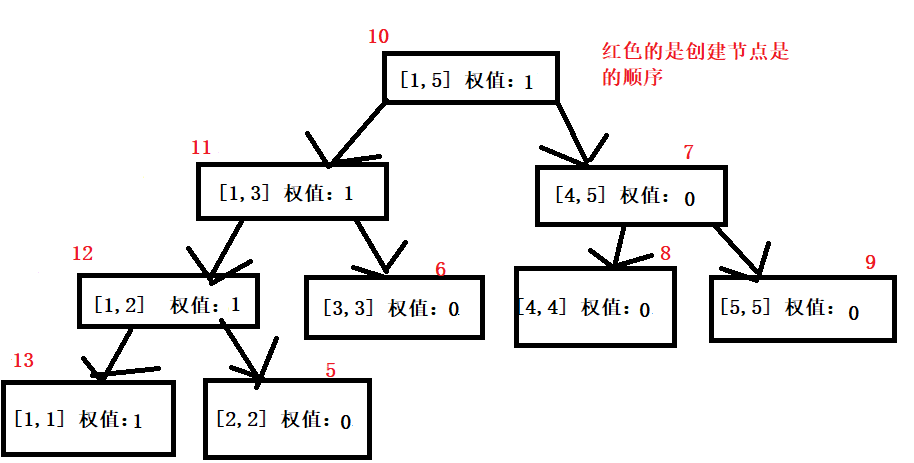
3、加一个2节点
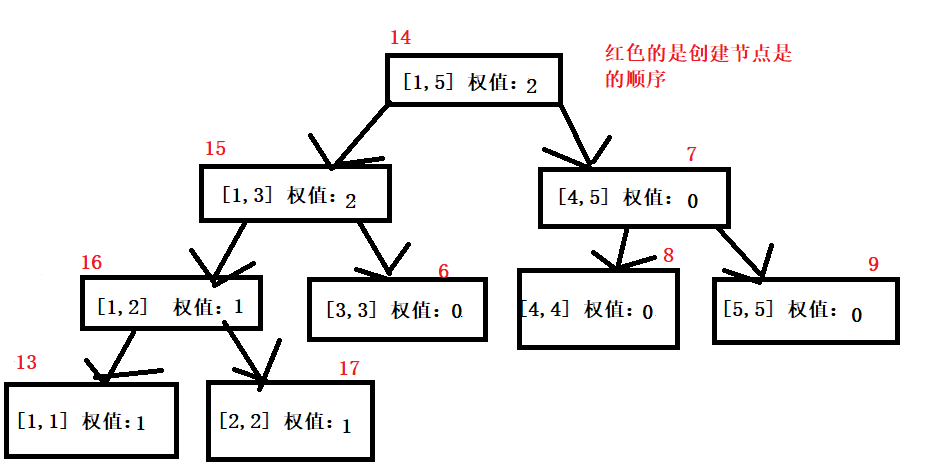
4、加一个节点3
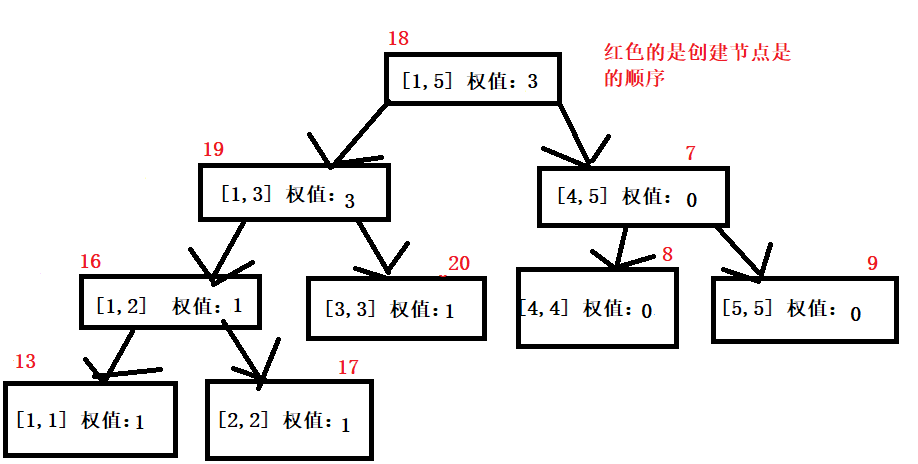
后面的4和5号节点就不写了,大家懂了就行。。。
四、主席树复杂度
插入一个点的时空复杂度都为O(log n),所以建立这颗主席树【权值线段树总体】的时空复杂度就是O(n log n),单次询问经过log n个节点,时间复杂度也为O(log n)
5、例题
K-th Number POJ - 2104
代码1:
1 #include<stdio.h> 2 #include<iostream> 3 #include<algorithm> 4 #include<string.h> 5 using namespace std; 6 const int maxn=1e5+10; 7 int cnt,ranks[maxn],v[maxn],root[maxn]; 8 struct shudui 9 { 10 int value,id; 11 }w[maxn]; 12 struct Node 13 { 14 int l,r,sum; 15 Node(){ 16 sum=0; 17 } 18 }tree[maxn*20]; 19 bool mmp(shudui x,shudui y) 20 { 21 return x.value<y.value; 22 } 23 void init() 24 { 25 cnt=1; 26 root[0]=0; 27 tree[0].l=tree[0].r=tree[0].sum=0; 28 } 29 void inserts(int num,int &rt,int l,int r) 30 { 31 tree[cnt++]=tree[rt]; 32 rt=cnt-1; 33 tree[rt].sum++; 34 if(l==r) return; 35 int mid=(l+r)>>1; 36 if(num<=mid) inserts(num,tree[rt].l,l,mid); 37 else inserts(num,tree[rt].r,mid+1,r); 38 } 39 int query(int i,int j,int k,int l,int r) 40 { 41 int d=tree[tree[j].l].sum-tree[tree[i].l].sum; 42 if(l==r) return l; 43 int mid=(l+r)>>1; 44 if(k <= d) return query(tree[i].l, tree[j].l, k, l, mid); //这里是小写的L,mid可不是数字1 45 else return query(tree[i].r, tree[j].r, k - d, mid + 1, r); 46 } 47 int main() 48 { 49 int n,m; 50 scanf("%d%d",&n,&m); 51 for(int i=1;i<=n;++i) 52 { 53 scanf("%d",&w[i].value); 54 w[i].id=i; 55 } 56 sort(w+1,w+1+n,mmp); 57 w[0].value=-1; 58 int j=1; 59 for(int i=1;i<=n;++i) 60 { 61 if(w[i].value!=w[i-1].value) 62 ranks[w[i].id]=j,v[j]=w[i].value,j++; 63 else ranks[w[i].id]=j-1; 64 } 65 init(); 66 for(int i=1;i<=n;++i) 67 { 68 //printf("%d %d\n",ranks[i],v[i]); 69 root[i]=root[i-1]; 70 inserts(ranks[i],root[i],1,n); 71 } 72 while(m--) 73 { 74 int l,r,x; 75 scanf("%d%d%d",&l,&r,&x); 76 printf("%d\n",v[query(root[l-1],root[r],x,1,n)]); 77 } 78 return 0; 79 }
代码2:
1 //洛谷 P3834 可持久化线段树(主席树) 2 3 #include<cstdio> 4 5 #include<cstring> 6 7 #include<algorithm> 8 9 using namespace std; 10 11 const int N=200005; 12 13 int n,m,q,t=0; 14 15 int a[N],b[N],root[N]; 16 17 struct node 18 19 { 20 21 int ls,rs,sum; 22 23 }tree[N*20]; 24 25 void disc() 26 27 { 28 29 int i; 30 31 sort(b+1,b+n+1); 32 33 m=unique(b+1,b+n+1)-(b+1); 34 35 for(i=1;i<=n;++i) 36 37 a[i]=lower_bound(b+1,b+m+1,a[i])-b; 38 39 } 40 41 42 43 //insert函数就是说:当前插入的数p,会影响节点x,所以把x节点的sum加1. 44 45 46 47 //节点x代表一个权值区间,影响x就是说p在节点x所代表的权值区间内。 48 49 //那么先把前一个树的对应区间的节点复制过来,再加1,就行了。 50 51 //可以结合刚才的图感性理解一下。 52 53 void insert(int y,int &x,int l,int r,int p) 54 55 { 56 57 x=++t; //t相当于是一个节点的地址,每个节点是不同的。 58 59 tree[x]=tree[y]; //复制前一个树的对应节点【它们代表的权值区间相同】。 60 61 tree[x].sum++; //给这个节点的sum加1.(这个1指的就是p) 62 63 if(l==r) return; //搜索到根节点就返回。 64 65 int mid=(l+r)>>1; 66 67 68 69 //判断在哪个区间继续插入。 70 71 if(p<=mid) insert(tree[y].ls,tree[x].ls,l,mid,p); 72 73 else insert(tree[y].rs,tree[x].rs,mid+1,r,p); 74 75 } 76 77 78 79 //k是查询第k小 80 81 //x和y相当于是树的节点的地址。而l和r就是这两个节点的权值区间。 82 83 //一开始query(root[l-1],root[r],1,m,k)。 84 85 //root[l-1]就是第l-1颗树的根节点。root[r]就是第r颗树的根节点。 86 87 //比较它们左儿子代表的区间中的数的个数,差值为delta。根据delta判断这两个节点一起往哪个方向跳。 88 89 //分析过程和刚才二分的过程一样。 90 91 int query(int x,int y,int l,int r,int k) 92 93 { 94 95 if(l==r) return l; //查到权值线段树的叶子节点就返回这个值。 96 97 int delta=tree[tree[y].ls].sum-tree[tree[x].ls].sum; 98 99 int mid=(l+r)>>1; 100 101 if(k<=delta) return query(tree[x].ls,tree[y].ls,l,mid,k); 102 103 else return query(tree[x].rs,tree[y].rs,mid+1,r,k-delta); 104 105 } 106 107 int main() 108 109 { 110 111 int l,r,i,k; 112 113 scanf("%d%d",&n,&q); 114 115 for(i=1;i<=n;++i) 116 117 { 118 119 scanf("%d",&a[i]); 120 121 b[i]=a[i]; 122 123 } 124 125 disc(); 126 127 for(i=1;i<=n;++i) 128 129 insert(root[i-1],root[i],1,m,a[i]); 130 131 for(i=1;i<=q;++i) 132 133 { 134 135 scanf("%d%d%d",&l,&r,&k); 136 137 138 139 //query函数返回的是第k小的权值。 140 141 //把这个权值转化为原来这个权值对应的数就行了。 142 143 printf("%d\n",b[query(root[l-1],root[r],1,m,k)]); 144 145 } 146 147 return 0; 148 149 }
参考博客:
https://blog.csdn.net/g21glf/article/details/82986968
https://blog.csdn.net/creatorx/article/details/75446472


