树状数组 && 板子
本文树状数组讲解转载于:https://www.cnblogs.com/xenny/p/9739600.html
本文新加内容为模板代码部分
1.什么是树状数组?
顾名思义,就是用数组来模拟树形结构呗。那么衍生出一个问题,为什么不直接建树?答案是没必要,因为树状数组能处理的问题就没必要建树。和Trie树的构造方式有类似之处。
2.树状数组可以解决什么问题
可以解决大部分基于区间上的更新以及求和问题。
3.树状数组和线段树的区别在哪里
树状数组可以解决的问题都可以用线段树解决,这两者的区别在哪里呢?树状数组的系数要少很多,就比如字符串模拟大数可以解决大数问题,也可以解决1+1的问题,但没人会在1+1的问题上用大数模拟。
4.树状数组的优点和缺点
修改和查询的复杂度都是O(logN),而且相比线段树系数要少很多,比传统数组要快,而且容易写。
缺点是遇到复杂的区间问题还是不能解决,功能还是有限。
5.树状数组的时间复杂度
树状数组建树时间复杂度为O(N)
树状数组查询和修改时间复杂度为O(logN)
一、树状数组介绍
二叉树大家一定都知道,如下图

如果每个父亲都存的是两个儿子的值,是不是就可以解决这类区间问题了呢。是的没错,但是这样的树形结构,叫做线段树。
那真的的树形结构是怎样的,和上图类似,但省去了一些节点,以达到用数组建树。
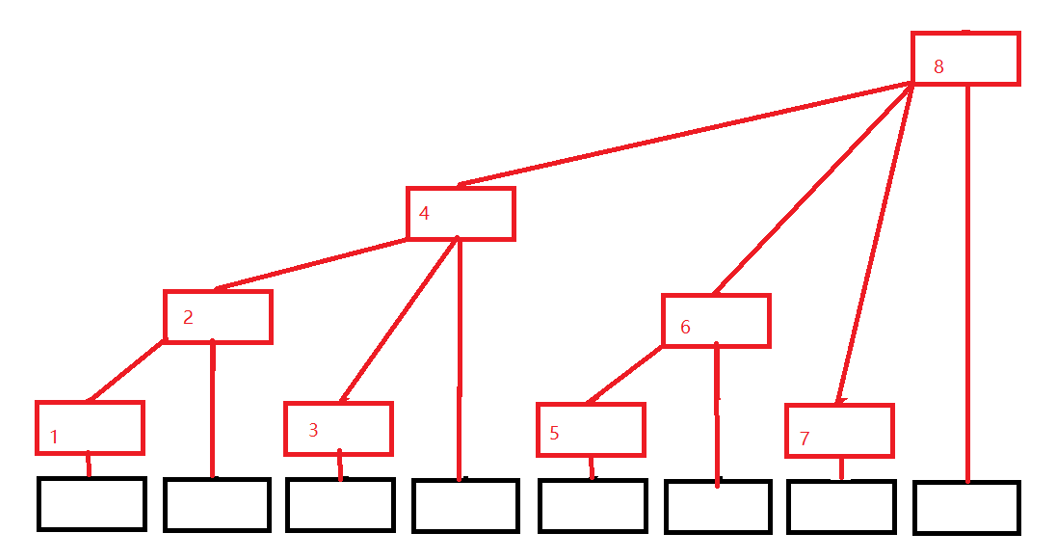
黑色数组代表原来的数组(下面用A[i]代替),红色结构代表我们的树状数组(下面用C[i]代替),发现没有,每个位置只有一个方框,令每个位置存的就是子节点的值的和,则有
- C[1] = A[1];
- C[2] = A[1] + A[2];
- C[3] = A[3];
- C[4] = A[1] + A[2] + A[3] + A[4];
- C[5] = A[5];
- C[6] = A[5] + A[6];
- C[7] = A[7];
- C[8] = A[1] + A[2] + A[3] + A[4] + A[5] + A[6] + A[7] + A[8];
可以发现,这颗树是有规律的
C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i]; //k为i的二进制中从最低位到高位连续零的长度,get_sum函数原理就是这个
例如i = 8(1000)时候,k = 3,可自行验证。
这个怎么实现求和呢,比如我们要找前7项和,那么应该是SUM = C[7] + C[6] + C[4];
而根据上面的式子,容易的出SUMi = C[i] + C[i-2k1] + C[(i - 2k1) - 2k2] + .....;(SUMi表示区间[1,i]内所有数之和)
这里的k1为i的“二进制中从最低位到高位连续零”,k2为(i-2k1)的“二进制中从最低位到高位连续零”,之后的也是这样
其实树状数组就是一个二进制上面的应用。
现在新的问题来了2^k(单独对一个i求2^k)该怎么求呢,不难得出2^k = i&(i^(i-1));但这个还是不好求出呀,前辈的智慧就出来了,2^k = i&(-i);
为什么呢?
这里利用的负数的存储特性,负数是以补码存储的,对于整数运算 x&(-x)有
● 当x为0时,即 0 & 0,结果为0;
●当x为奇数时,最后一个比特位为1,取反加1没有进位,故x和-x除最后一位外前面的位正好相反,按位与结果为0。结果为1。
●当x为偶数,且为2的m次方时,x的二进制表示中只有一位是1(从右往左的第m+1位),其右边有m位0,故x取反加1后,从右到左第有m个0,第m+1位及其左边全是1。这样,x& (-x) 得到的就是x。
●当x为偶数,却不为2的m次方的形式时,可以写作x= y * (2^k)。其中,y的最低位为1。实际上就是把x用一个奇数左移k位来表示。这时,x的二进制表示最右边有k个0,从右往左第k+1位为1。当对x取反时,最右边的k位0变成1,第k+1位变为0;再加1,最右边的k位就又变成了0,第k+1位因为进位的关系变成了1。左边的位因为没有进位,正好和x原来对应的位上的值相反。二者按位与,得到:第k+1位上为1,左边右边都为0。结果为2^k。
总结一下:x&(-x),当x为0时结果为0;x为奇数时,结果为1;x为偶数时,结果为x中2的最大次方的因子。
而且这个有一个专门的称呼,叫做lowbit,即取2^k。
二、模板代码
1、建立树状数组、修改某位置点的大小、询问区间内所有数之和
上面已经解释了如何用树状数组求区间和,那么如果我们要更新某一个点的值呢,还是一样的,上面说了C[i] = A[i - 2k+1] + A[i - 2k+2] + ... + A[i],那么如果我们更新某个A[i]的值,则会影响到所有包含有A[i]位置。如果求A[i]包含哪些位置里呢,同理有
A[i] 包含于 C[i + 2k]、C[(i + 2k) + 2k]...; //update函数的原理就是这个
模板例题:hdu 1166
代码:

1 #include<stdio.h> 2 #include<iostream> 3 #include<algorithm> 4 #include<string.h> 5 using namespace std; 6 const int maxn=5e5+10; 7 int v,tree[maxn]; 8 int n; 9 int lowbit(int x) 10 { 11 return x&(-x); 12 } 13 void update(int i,int x) 14 { 15 while(i<=n) 16 { 17 tree[i]+=x; 18 i+=lowbit(i); 19 } 20 } 21 int get_sum(int i) //获取区间[1,i]所有数之和 22 { 23 int ans=0; 24 while(i>0) 25 { 26 ans+=tree[i]; 27 i-=lowbit(i); 28 } 29 return ans; 30 } 31 int main() 32 { 33 int t,p=0; 34 scanf("%d",&t); 35 while(t--) 36 { 37 memset(tree,0,sizeof(tree)); 38 scanf("%d",&n); 39 for(int i=1;i<=n;++i) 40 { 41 scanf("%d",&v); 42 update(i,v); 43 } 44 char s[20]; 45 int x,y; 46 printf("Case %d:\n",++p); 47 while(~scanf("%s",s)) 48 { 49 if(s[0]=='E') break; 50 else if(s[0]=='Q') 51 { 52 scanf("%d%d",&x,&y); 53 printf("%d\n",get_sum(y)-get_sum(x-1)); 54 } 55 else if(s[0]=='A') 56 { 57 scanf("%d%d",&x,&y); 58 update(x,y); 59 } 60 else if(s[0]=='S') 61 { 62 scanf("%d%d",&x,&y); 63 update(x,-y); 64 } 65 } 66 } 67 return 0; 68 }
2、建立树状数组、区间更新、单点查询:
如果题目是让你把x-y区间内的所有值全部加上k或者减去k,然后查询操作是问某个点的值,这种时候该怎么做呢。如果是像上面的树状数组来说,就必须把x-y区间内每个值都更新,这样的复杂度肯定是不行的,这个时候,就不能再用数据的值建树了,这里我们引入差分,利用差分建树。
假设我们规定A[0] = 0;
则有 A[i] = Σij = 1D[j];(D[j] = A[j] - A[j-1]),即前面i项的差值和,这个有什么用呢?例如对于下面这个数组
- A[] = 1 2 3 5 6 9
- D[] = 1 1 1 2 1 3
如果我们把[2,5]区间内值加上2,则变成了
- A[] = 1 4 5 7 8 9
- D[] = 1 3 1 2 1 1
发现了没有,当某个区间[x,y]值改变了,区间内的差值是不变的,只有D[x]和D[y+1]的值发生改变,至于为什么我想我就不用解释了吧。
所以我们就可以利用这个性质对D[]数组建立树状数组。
代码:

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=5e5+10; 7 int n,m,tree[maxn]; 8 int lowbit(int x) 9 { 10 return x&(-x); 11 } 12 void update(int x,int y) 13 { 14 while(x<=n) 15 { 16 tree[x]+=y; 17 x+=lowbit(x); 18 } 19 } 20 int get_sum(int x) 21 { 22 int ans=0; 23 while(x>0) 24 { 25 ans+=tree[x]; 26 x-=lowbit(x); 27 } 28 return ans; 29 } 30 int main() 31 { 32 while(~scanf("%d%d",&n,&m)) 33 { 34 memset(tree,0,sizeof(tree)); 35 int start,now; 36 scanf("%d",&start); 37 update(1,start); 38 for(int i=2; i<=n; ++i) 39 { 40 scanf("%d",&now); 41 update(i,now-start); 42 start=now; 43 } 44 while(m--) 45 { 46 int x,y,z; 47 scanf("%d",&x); 48 if(x==1) 49 { 50 scanf("%d%d%d",&x,&y,&z); 51 update(x,z); 52 update(y+1,-z); 53 } 54 else 55 { 56 scanf("%d",&x); 57 printf("%d\n",get_sum(x)); 58 } 59 } 60 61 } 62 return 0; 63 }
3、建立树状数组、区间修改、区间查询
上面我们说的差值建树状数组,得到的是某个点的值,那如果我既要区间更新,又要区间查询怎么办。这里我们还是利用差分,由上面可知
∑ni = 1A[i] = ∑ni = 1 ∑ij = 1D[j];
则A[1]+A[2]+...+A[n]
= (D[1]) + (D[1]+D[2]) + ... + (D[1]+D[2]+...+D[n])
= n*D[1] + (n-1)*D[2] +... +D[n]
= n * (D[1]+D[2]+...+D[n]) - (0*D[1]+1*D[2]+...+(n-1)*D[n])
所以上式可以变为∑ni = 1A[i] = n*∑ni = 1D[i] - ∑ni = 1( D[i]*(i-1) );
如果你理解前面的都比较轻松的话,这里也就知道要干嘛了,维护两个数状数组,sum1[i] = D[i],sum2[i] = D[i]*(i-1);
例题:A Simple Problem with Integers
代码:

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<algorithm> 5 using namespace std; 6 const int maxn=1e5+10; 7 typedef long long ll; 8 ll n,m,tree[maxn],tree2[maxn]; 9 ll lowbit(ll x) 10 { 11 return x&(-x); 12 } 13 void update(ll x,ll y) 14 { 15 ll i=x-1; 16 while(x<=n) 17 { 18 tree[x]+=y; 19 tree2[x]+=i*y; 20 x+=lowbit(x); 21 } 22 } 23 ll get_sum(ll x) 24 { 25 ll ans=0; 26 ll i=x; 27 while(x>0) 28 { 29 ans=ans+i*tree[x]-tree2[x]; 30 x-=lowbit(x); 31 } 32 return ans; 33 } 34 int main() 35 { 36 while(~scanf("%lld%lld",&n,&m)) 37 { 38 memset(tree,0,sizeof(tree)); 39 memset(tree2,0,sizeof(tree2)); 40 ll start,now; 41 scanf("%lld",&start); 42 update(1,start); 43 for(ll i=2; i<=n; ++i) 44 { 45 scanf("%lld",&now); 46 update(i,now-start); 47 start=now; 48 } 49 while(m--) 50 { 51 char s[5]; 52 ll x,y,z; 53 scanf("%s",s); 54 if(s[0]=='C') 55 { 56 scanf("%lld%lld%lld",&x,&y,&z); 57 update(x,z); 58 update(y+1,-z); 59 } 60 else 61 { 62 scanf("%lld%lld",&x,&y); 63 printf("%lld\n",get_sum(y)-get_sum(x-1)); 64 } 65 } 66 } 67 return 0; 68 }



