考研路茫茫——单词情结 HDU - 2243 AC自动机 && 矩阵快速幂

背单词，始终是复习英语的重要环节。在荒废了3年大学生涯后，Lele也终于要开始背单词了。
一天，Lele在某本单词书上看到了一个根据词根来背单词的方法。比如"ab",放在单词前一般表示"相反，变坏，离去"等。

于是Lele想，如果背了N个词根，那这些词根到底会不会在单词里出现呢。更确切的描述是：长度不超过L，只由小写字母组成的，至少包含一个词根的单词，一共可能有多少个呢？这里就不考虑单词是否有实际意义。

比如一共有2个词根 aa 和 ab ，则可能存在104个长度不超过3的单词，分别为
(2个) aa,ab,
(26个)aaa,aab,aac...aaz,
(26个)aba,abb,abc...abz,
(25个)baa,caa,daa...zaa,
(25个)bab,cab,dab...zab。

这个只是很小的情况。而对于其他复杂点的情况，Lele实在是数不出来了，现在就请你帮帮他。

Input本题目包含多组数据，请处理到文件结束。
每组数据占两行。
第一行有两个正整数N和L。(0<N<6,0<L<2^31)
第二行有N个词根，每个词根仅由小写字母组成，长度不超过5。两个词根中间用一个空格分隔开。
Output对于每组数据，请在一行里输出一共可能的单词数目。
由于结果可能非常巨大，你只需要输出单词总数模2^64的值。
Sample Input

2 3
aa ab
1 2
a

Sample Output

104
52

 

 

 

先找出来长度小于等于L的串，一共有多少个。然后找出来长度小于等于L的串不包含模式串有多少个

两者之差就是答案

 

题意：
问出现这几个模式串，长度小于等于L的字符串数量有多少

题解：

建议提前看一下DNA Sequence POJ - 2778
和DNA Sequence POJ - 2778 （问不出现这几个模式串，长度等于L的字符串数量有多少） 这道题差不多。
只需要转化一下：
先求出来长度小于等于L所有串的数量，然后再求一下不出现这几个模式串，长度小于等于L的字符串数量有多少
假设用ac自动机跑出来的矩阵是A
那么就求出来A,A^1,A^2...A^L.每一个矩阵第一行之和。

这就只需要在A矩阵中增加一列，这一列都赋值为1.在对应也要把增加那一行的其他位置赋值为0

例如

原来A=  | 1 2 |       =>>   转化后    A= |1 2 1 |

              | 3 4 |                                    | 3 4 1 |

                                                           |0 0 1 |

这样最后跑出来的A^L的第一行所有数之和就是最后答案

 

至于为什么，看下面：

 

 

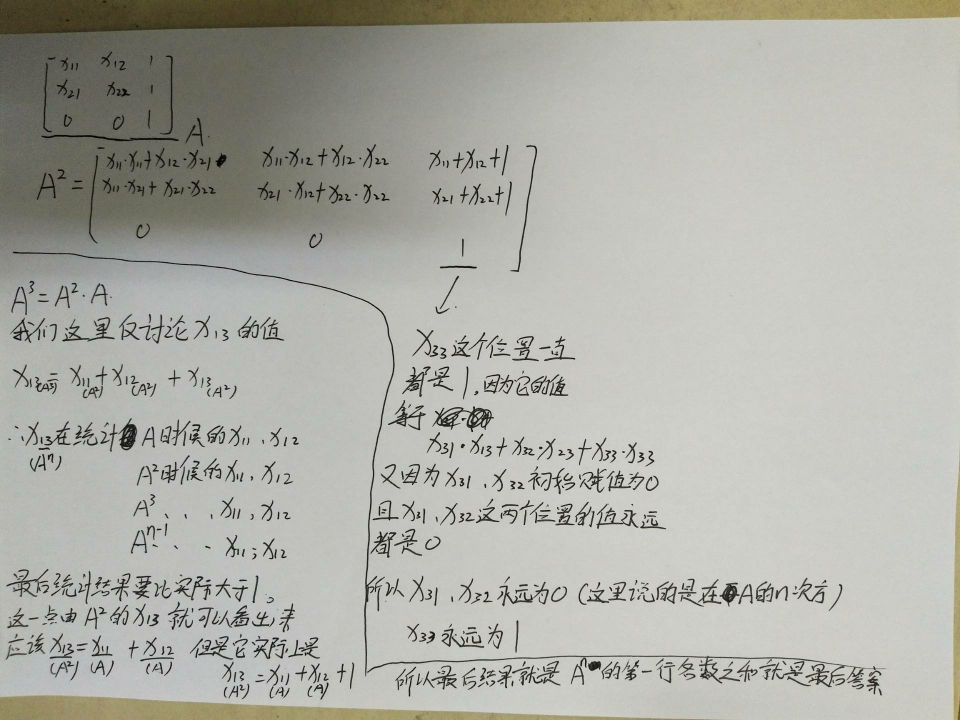
全部串的数量：
26^1 + 26^2 + 26^3 + … + 26^n，也用矩阵快速幂计算。f(n) = 26 * f(n - 1) + 26。
| f(n - 1) 1 |
| 0 0        |
系数矩阵：
| 26 0 |
| 26 1 |
相乘得到：
| f(n) 1 |
| 0 0    |

两者之差就是结果

 

代码：

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=70;
const int N=26;
const int mod=100000;
typedef long long ll;
typedef unsigned long long ull;
ull m;
struct Matrix
{
    unsigned long long mat[40][40];
    int n;
    Matrix(){}
    Matrix(int _n)
    {
        n=_n;
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                mat[i][j] = 0;
    }
    Matrix operator *(const Matrix &b)const
    {
        Matrix ret = Matrix(n);
        for(int i=0;i<n;i++)
            for(int j=0;j<n;j++)
                for(int k=0;k<n;k++)
                    ret.mat[i][j]+=mat[i][k]*b.mat[k][j];
        return ret;
    }
};
unsigned long long pow_m(unsigned long long a,int n)
{
    unsigned long long ret=1;
    unsigned long long tmp = a;
    while(n)
    {
        if(n&1)ret*=tmp;
        tmp*=tmp;
        n>>=1;
    }
    return ret;
}
Matrix pow_M(Matrix a,int n)
{
    Matrix ret = Matrix(a.n);
    for(int i=0;i<a.n;i++)
        ret.mat[i][i] = 1;
    Matrix tmp = a;
    while(n)
    {
        if(n&1)ret=ret*tmp;
        tmp=tmp*tmp;
        n>>=1;
    }
    return ret;
}
struct Trie
{
    ull next[maxn][N],fail[maxn],ends[maxn];
    ull root,L;
    ull New_node() //创建一个新节点
    {
        for(ull i=0; i<N; ++i)
        {
            next[L][i]=-1;
        }
        ends[L++]=0;
        return L-1;
    }
    void init()  //创建根节点
    {
        L=0;
        root=New_node();
    }
    void inserts(char s[])  //往字典树里面插入新字符串
    {
        ull len=strlen(s);
        ull now=root;
        for(ull i=0; i<len; ++i)
        {
            if(next[now][s[i]-'a']==-1)
                next[now][s[i]-'a']=New_node();
            now=next[now][s[i]-'a'];
        }
        ends[now]=1;
    }
    void build()
    {
        queue<ull>r;
        fail[root]=root;
        for(ull i=0; i<N; ++i)
        {
            if(next[root][i]==-1)
            {
                next[root][i]=root;
            }
            else
            {
                fail[next[root][i]]=root;
                r.push(next[root][i]);
            }
        }
        while(!r.empty())
        {
            ull now=r.front();
            r.pop();
            if(ends[fail[now]])
            {
                ends[now]=1;
            }
            for(ull i=0; i<N; ++i)
            {
                if(next[now][i]==-1)
                {
                    next[now][i]=next[fail[now]][i];  //叶节点处没有设置失败节点而是往next上接了一段，这个时候
                    //这个fail里面的值已经在下面的else里面放过东西了
                }
                else
                {
                    fail[next[now][i]]=next[fail[now]][i];  //此节点的子节点的失败节点就是此节点失败节点对应字符位置
                    r.push(next[now][i]);
                }
            }
        }
    }
    Matrix Build_c()
    {
        Matrix res=Matrix(L+1);
        for(ull i=0; i<L; ++i)
        {
            for(ull j=0; j<N; ++j)
            {
                if(ends[next[i][j]]==0)
                {
                    res.mat[i][next[i][j]]++;
                }
            }
        }
        for(ull i=0;i<L+1;++i)
            res.mat[i][L]=1;
        return res;
    }
};
char s[10];
Trie ac;
Matrix pow_M(Matrix a,ull n)
{
    Matrix ret = Matrix(a.n);
    for(ull i = 0; i < ret.n; i++)
        ret.mat[i][i]=1;
    Matrix tmp=a;
    while(n)
    {
        if(n&1)ret=ret*tmp;
        tmp=tmp*tmp;
        n>>=1;
    }
    return ret;
}
int main()
{
    ull n;
    while(~scanf("%llu%llu",&n,&m))
    {
        ac.init();
        while(n--)
        {
            scanf("%s",s);
            ac.inserts(s);
        }
        Matrix two=Matrix(2); /*求出总共有多少单词数*/
        two.mat[0][0]=26;
        two.mat[0][1]=1;
        two.mat[1][1]=1;
        two=pow_M(two,m);
        ull tot=two.mat[0][1]*26;

        ac.build();            /*求不满足题意得单词数量*/
        Matrix ans=ac.Build_c();
        ans=pow_M(ans,m);
        ull sum=0;
        for(ull i=0;i<ans.n;++i)
            sum+=ans.mat[0][i];
        sum--;

        printf("%llu\n",tot-sum);
    }
    return 0;
}