K - Japan（线段树）

小A的楼房外有一大片施工工地，工地上有N栋待建的楼房。每天，这片工地上的房子拆了又建、建了又拆。他经常无聊地看着窗外发呆，数自己能够看到多少栋房子。
　　为了简化问题，我们考虑这些事件发生在一个二维平面上。小A在平面上(0,0)点的位置，第i栋楼房可以用一条连接(i,0)和(i,Hi)的线段表示，其中Hi为第i栋楼房的高度。如果这栋楼房上任何一个高度大于0的点与(0,0)的连线没有与之前的线段相交，那么这栋楼房就被认为是可见的。
　　施工队的建造总共进行了M天。初始时，所有楼房都还没有开始建造，它们的高度均为0。在第i天，建筑队将会将横坐标为Xi的房屋的高度变为Yi(高度可以比原来大—修建，也可以比原来小—拆除，甚至可以保持不变—建筑队这天什么事也没做)。请你帮小A数数每天在建筑队完工之后，他能看到多少栋楼房？
输入：
第一行两个正整数N,M
　　接下来M行，每行两个正整数Xi,Yi
输出：
M行，第i行一个整数表示第i天过后小A能看到的楼房有多少栋

Test case (case number): (number of crossings)
Sample Input

3 4
2 4
3 6
1 1000000000
1 1

    Sample Output

1
1
1
2
数据约定
　　对于所有的数据1<=Xi<=N，1<=Yi<=10^9
N,M<=100000

题意：说简单点就是一个人站在原点，他的前方有好些房子，只有后边的房子到原点的斜率大于前边的房子到原点的最大斜率我们才可以看到它，他的视线是在一条直线上

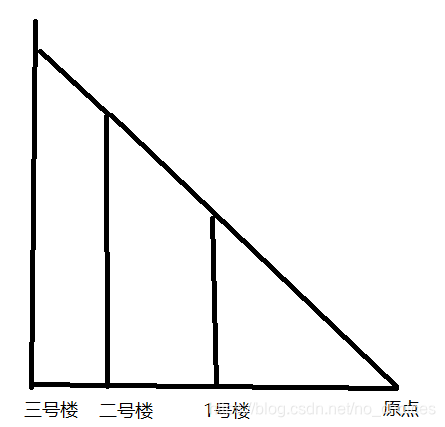
因为二号楼的斜率和一号楼的斜率是一样的，所以我们只能看到一号楼，看不到二号楼，但是三号楼到原点的斜率显然大于前面面所有点的斜率（图中没花出），所以我们还可以看到三号楼
代码操作：
我们要开一个变量专门去存这个区间内的最大斜率value，再开一个去存这个区间内的可见房子数目cnt
如果我们改变一个点的高度，那么这个点到原点这一部分（右侧）距离的房子可见数不会改变，改变的只有后面的（称为左）。对于后面的，如果已经递归到底层叶子节点，那么如果该点的斜率大于右侧区间（也是一个点）最大的斜率，则可以被看到，返回1，反之返回0
在每个叶节点中只要那个点有高度，就给他的的cnt赋值为1

代码：

#include<stdio.h>
#include<string.h>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=100005;
int cnt[maxn<<2];
double value[maxn<<2];
int cal(double val,int l,int r,int rt)
{
    if(l==r) return value[rt]>val;
    int m=(l+r)>>1;
    //if(l==r) return value[rt]>val;
    //int m=(l+r)>>1;
    if(value[rt<<1]<=val) return cal(val,m+1,r,rt<<1|1);
    //if(value[rt<<1]<=val) return cal(val,m+1,r,rt<<1|1);
    //else return cnt[rt]-cnt[rt<<1]+cal(val,1,m,rt<<1);
    else return cnt[rt]-cnt[rt<<1]+cal(val,l,m,rt<<1);   //这里是L不是数字1，卧槽。。
}
//void update(int L,double C,int l,int r,int rt)
//{
//    if(l==r)
//    {
//        cnt[rt]=1;
//        value[rt]=C;
//        return;
//    }
//    int m=(l+r)>>1;
//    if(L<=m) update(L,C,1,m,rt<<1);
//    else update(L,C,m+1,r,rt<<1|1);
//    value[rt]=max(value[rt<<1],value[rt<<1|1]);
//    cnt[rt]=cnt[rt<<1]+cal(value[rt<<1],m+1,r,rt<<1|1);
//}
//int cal(double val,int l,int r,int rt){


//
//}
void update(int loc,double val,int l,int r,int rt){
    if(l==r){
        cnt[rt]=1;
        value[rt]=val;
        return;
    }
    int mid=(l+r)>>1;
    if(loc<=mid) update(loc,val,l,mid,rt<<1);
    else         update(loc,val,mid+1,r,rt<<1|1);
    value[rt]=max(value[rt<<1],value[rt<<1|1]);
    cnt[rt]=cnt[rt<<1]+cal(value[rt<<1],mid+1,r,rt<<1|1);
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        update(x,double(y*1.0/x),1,n,1);
        printf("%d\n",cnt[1]);
    }
    return 0;
}