HDU -1151 二分匹配与有向无环图不相交最小路径覆盖数

题意：

考虑一个小镇，那里的所有街道都是单向的，并且每条街道都从一个路口通往另一个路口。还众所周知，从一个十字路口开始，穿过城镇的街道，您将永远无法到达同一十字路口，即，城镇的街道没有环。

基于这些假设，您的任务是编写一个程序，以找到可以降落在城镇上的伞兵的最小数量，并以不止一个伞兵不交叉路口的方式（也就是说一个十字路口只能到达一次）访问该镇的所有十字路口。每个伞兵都会降落在一个十字路口，并可以沿着城镇街道访问其他十字路口。每个伞兵的起始十字路口都没有限制。

问你把所有十字路口都走一遍需要的最少伞兵数量 

 

题解：

那么很显然像1->2->3->4这样的图，只需要一个机器人就可以了。我们这个时候可以利用拆点就是把{1}拆成两个点{1，1`},也相当于复制了一个1

本题可以不考虑为啥这一道题目是二分图路径覆盖，我们可以推出来。题目上面说士兵可以从一个城市走到另一个城市，一直到
不能走。那么可以说像1->2->3这一条路只需要一个士兵，这是因为1与2相连，2与3相连，所以用其他点减去有几条匹配边就是结果了（假设1，2和2，3是两条匹配边）
可是二分图上的匹配一个点只能用一次，那么我们就可以通过拆点来实现我们的方法

 

证明：

 

 

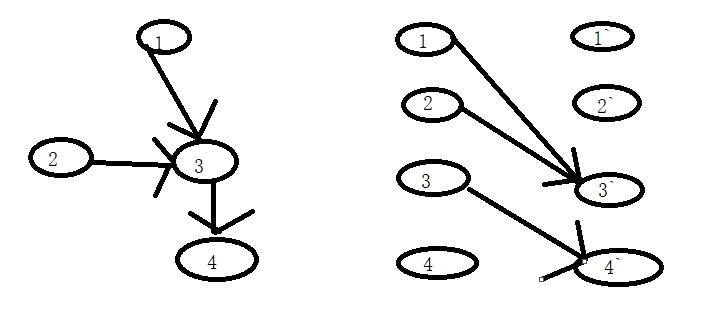
上图中,对应左边的DAG建立构造右边的二分图,可以找到二分图的一个最大匹配M:1-3',3-4',那么M中的这两条匹配边怎样对应DAG中的路径的边?
使二分图中一条边对应DAG中的一条有向边,1-3'对应DAG图中的有向边1->3,这样DAG中1就会有一个后继顶点(3会是1的唯一后继,因为二分图中一个顶点至多关联一条边!),
所以1不会成为DAG中一条路径中的结尾顶点,同样,3-4'对应DAG中3->4,3也不会成为结尾顶点,那么原图中总共4个顶点,减去2个有后继的顶点,就剩下没有后继的顶点,即DAG路径的结尾顶点,
而每个结尾顶点正好对应DAG中的一条路径,二分图中寻找最大匹配M,就是找到了对应DAG中的非路径结尾顶点的最大数目,那么DAG中顶点数-|M|就是DAG中结尾顶点的最小数目,即DAG的最小路径覆盖数.
本题目求的是“最小覆盖数”，而不是“最小覆盖”
上一个图的最小覆盖是3，（这里说的是原图）因为他只能找出来一条边，之后用4（总节点）-1（最大匹配）=3

 

代码：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
const int maxn=210;
vector<int>str[maxn];
int n,match[maxn],visit[maxn];
int dfs_solve(int x)
{
    int len=str[x].size();
    for(int i=0;i<len;++i)
    {
        int v=str[x][i];
        if(!visit[v])
        {
            visit[v]=1;
            if(match[v]==0 || dfs_solve(match[v]))
            {
                match[v]=x;
                return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        int m;
        scanf("%d",&m);
        while(m--)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            str[u].push_back(v);
        }
        int sum=0;

        memset(match,0,sizeof(match));
        for(int i=1;i<=n;++i)
        {
            memset(visit,0,sizeof(visit));
            sum+=dfs_solve(i);
        }
        //printf("%d\n",sum);
        printf("%d\n",n-sum);
//        printf("-------------\n");
//        for(int i=1;i<=n;++i)
//        {
//            printf("%d %d\n",i,match[i]);
//        }
//        printf("---------------\n");
        for(int i=1;i<=n;++i)
            str[i].clear();
    }
    return 0;
}