二分图匹配问题
一、
二分图基础:
参考链接:https://blog.csdn.net/jeryjeryjery/article/details/79596922
https://www.cnblogs.com/penseur/archive/2013/06/16/3138981.html
什么叫二分图:给你一些点,其中这些点之间的某两个点是相连的。如果你可以把全部点分成两个集合 且 每个集合的任意两个点之间没有连线
也就是说对于任意一条边它的两个点不能来自于一个集合,就比如:
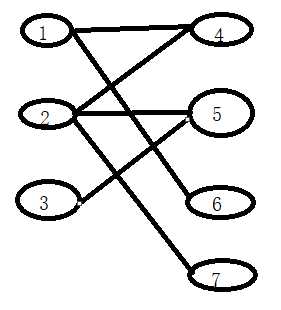
1,2,3一个集合,其他点一个集合就是二分图!
染色法判断是否为一个二分图:https://blog.csdn.net/li13168690086/article/details/81506044
算法过程:用两种颜色,对所有顶点逐个染色,且相邻顶点染不同的颜色,如果发现相邻顶点染了同一种颜色,就认为此图不为二分图。 当所有顶点都 被染色,且没有发现同色的相邻顶点,就退出。
以NYOJ 1015 二部图为例题:
代码:

1 #include <iostream> 2 #include <algorithm> 3 #include <string.h> 4 #include <stdio.h> 5 #include <math.h> 6 using namespace std; 7 const int N = 505; 8 int m,n; 9 int color[N]; 10 int edge[N][N]; 11 bool dfs(int v, int c){ 12 color[v] = c; //将当前顶点涂色 13 for(int i = 0; i < n; i++){ //遍历所有相邻顶点,即连着的点 14 if(edge[v][i] == 1){ //如果顶点存在 15 if(color[i] == c) //如果颜色重复,就返回false 16 return false; 17 if(color[i] == 0 && !dfs(i,-c)) //如果还未涂色,就染上相反的颜色-c,并dfs这个顶点,进入下一层 18 return false; //返回false 19 } 20 } 21 return true; //如果所有顶点涂完色,并且没有出现同色的相邻顶点,就返回true 22 } 23 void solve(){ 24 for(int i = 0; i < n; i++){ 25 if(color[i] == 0){ 26 if(!dfs(i, 1)){ 27 printf("NOT BICOLORABLE.\n"); 28 return; 29 } 30 } 31 } 32 printf("BICOLORABLE.\n"); 33 } 34 int main(){ 35 int u,v; 36 while(cin >> n >> m){ 37 memset(color, 0, sizeof(color)); 38 memset(edge, 0, sizeof(edge)); 39 for(int i = 0; i < m; i++){ 40 cin >> u >> v; //因为是无向图,所以要往两个方向添加边 41 edge[u][v] = 1; //正着添加 42 edge[v][u] = 1; //反着添加 43 } 44 solve(); 45 } 46 return 0; 47 }
什么叫匹配:图中匹配的定义是指,这个图的一个边的集合,集合中任意两条边都没有公共的顶点,则称这个边集为一个匹配。我们称匹配中的边匹 配边,边中的点为匹配点;未在匹配中的边为非匹配边,边中的点为未匹配点。就比如:

这就是一个匹配,每一个点只能使用一次,但是它并不是最大匹配,因为我们可以让2和8相连,这样就会多一条匹配边3->5
要注意所有匹配边都是原来图中存在的边,只是我们选择了这些边中的某几条
最大匹配: 一个图中所有匹配中,所含匹配边数最大的匹配称为最大匹配。
完美匹配: 如果一个图的某个匹配中,图的所有顶点都是匹配点,那么这个匹配就是完美匹配。很显然,完美匹配一定是最大匹配,但是并不是所有的 图都存在完美匹配。
交替路: 从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边、匹配边…,形成这样的交替进行的路径成为交替路。
什么是增广路: 从一个未匹配点出发,走交替路,如果途径一个未匹配点(出发点不算),则这样一条交替路称为增广路。增广路有一个重要的特性,就 是非匹配边要比匹配边多一条(从未匹配点出发,以未匹配点结束,走交替路,显然非匹配边多一条),此时,我们可以让增广路中的匹 配边和非匹配边调换位置,匹配边变为非匹配边,非匹配边变为匹配边,这样匹配边的数量就会加1,并且由于中间的匹配节点不存在其 他相连的匹配边,所以这样做不会破坏匹配的性质,保证了交换的正确性。
匈牙利算法: 算法就是根据增广路的思想,以一个未匹配的节点出发,遍历图,不断的寻找增广路来扩充匹配的边数,直到不能扩充为止。根据遍历图的 方式不同,匈牙利算法可以分为dfs(深度遍历)和bfs(广度遍历)的实现。
匈利牙利算法复杂度:这个问题既可以利用最大流算法解决也可以用匈牙利算法解决。如果用最大流算法中的Edmonds-karp算法解决,因为时间复杂度 为O(n*m*m),n为点数,m为边数,会超时,利用匈牙利算法,时间复杂度为O(n*m),时间复杂度小,不会超时。
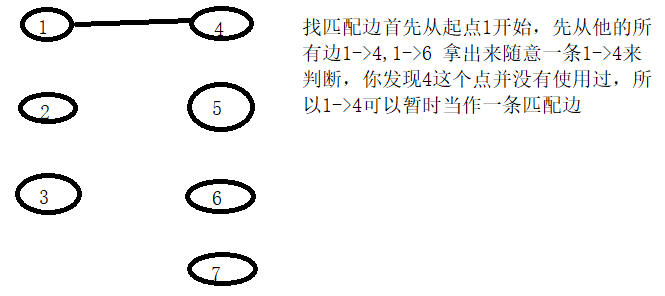

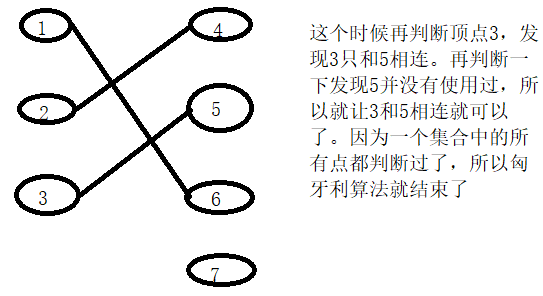
以HDU - 1083 Courses为例子:
题意:给你p个课程和n个学生,你可不可以从这k个学生中找出来p个学生,使得每一个学生负责一个课程。后面会给出课程和上这个课的学生
只要这个学生上这个课就可以负责这个课程
代码:

1 #include<stdio.h> 2 #include<algorithm> 3 #include<string.h> 4 #include<iostream> 5 #include<queue> 6 using namespace std; 7 const int maxn=305; 8 int match[maxn],visit[maxn],n,m,grap[maxn][maxn]; 9 int dfs_solve(int x) 10 { 11 for(int i=1;i<=n;++i) 12 { 13 if(grap[x][i] && !visit[i]) 14 { 15 visit[i]=1; 16 if(match[i]==0 || dfs_solve(match[i])) 17 { 18 match[i]=x; 19 return 1; 20 } 21 } 22 } 23 return 0; 24 } 25 int hungran() 26 { 27 memset(match,0,sizeof(match)); 28 int sum=0; 29 for(int i=1;i<=m;++i) 30 { 31 memset(visit,0,sizeof(visit)); 32 sum+=dfs_solve(i); 33 } 34 return sum; 35 } 36 int main() 37 { 38 int t; 39 scanf("%d",&t); 40 while(t--) 41 { 42 scanf("%d%d",&m,&n); 43 memset(grap,0,sizeof(grap)); 44 for(int i=1;i<=m;++i) 45 { 46 int q; 47 scanf("%d",&q); 48 while(q--) 49 { 50 int w; 51 scanf("%d",&w); 52 grap[i][w]=1; 53 } 54 } 55 int ans=hungran(); 56 if(ans==m) 57 { 58 printf("YES\n"); 59 } 60 else printf("NO\n"); 61 } 62 return 0; 63 }
Hopcroft-Karp算法:这个算法的时间复杂度为O(n^(1/2)*m)。该算法是对匈牙利算法的优化。利用匈牙利算法一次只能找到一条增广路径,Hopcroft-K arp就提出一次找到多条不相交的增广路径(不相交就是没有公共点和公共边的增广路径),然后根据这些增广路径添加多个匹配。 说白了,就是批量处理!
具体过程看下图:
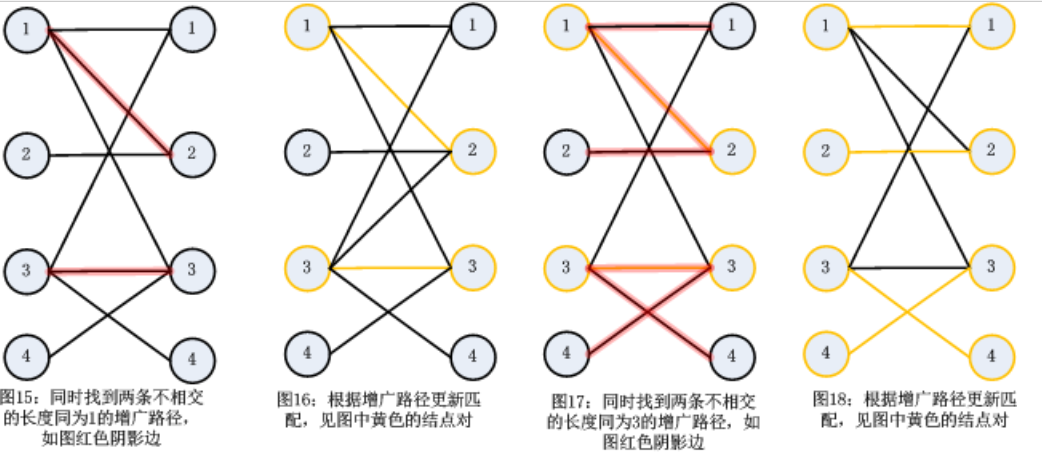
还是以上一道题为例子:

1 #include<iostream> 2 #include<queue> 3 using namespace std; 4 const int MAXN=500;// 最大点数 5 const int INF=1<<28;// 距离初始值 6 int bmap[MAXN][MAXN];//二分图 7 8 int cx[MAXN];//cx[i]表示左集合i顶点所匹配的右集合的顶点序号 9 int cy[MAXN]; //cy[i]表示右集合i顶点所匹配的左集合的顶点序号 10 11 int nx,ny; 12 int dx[MAXN]; 13 int dy[MAXN]; 14 int dis; 15 bool bmask[MAXN]; 16 //寻找 增广路径集 17 bool searchpath() 18 { 19 queue<int>Q; 20 dis=INF; 21 memset(dx,-1,sizeof(dx)); 22 memset(dy,-1,sizeof(dy)); 23 for(int i=1;i<=nx;i++) 24 { 25 //cx[i]表示左集合i顶点所匹配的右集合的顶点序号 26 if(cx[i]==-1) 27 { 28 //将未遍历的节点 入队 并初始化次节点距离为0 29 Q.push(i); 30 dx[i]=0; 31 } 32 } 33 //广度搜索增广路径 34 while(!Q.empty()) 35 { 36 int u=Q.front(); 37 Q.pop(); 38 if(dx[u]>dis) break; 39 //取右侧节点 40 for(int v=1;v<=ny;v++) 41 { 42 //右侧节点的增广路径的距离 43 if(bmap[u][v]&&dy[v]==-1) 44 { 45 dy[v]=dx[u]+1; //v对应的距离 为u对应距离加1 46 if(cy[v]==-1) dis=dy[v]; 47 else 48 { 49 dx[cy[v]]=dy[v]+1; 50 Q.push(cy[v]); 51 } 52 } 53 } 54 } 55 return dis!=INF; 56 } 57 58 //寻找路径 深度搜索 59 int findpath(int u) 60 { 61 for(int v=1;v<=ny;v++) 62 { 63 //如果该点没有被遍历过 并且距离为上一节点+1 64 if(!bmask[v]&&bmap[u][v]&&dy[v]==dx[u]+1) 65 { 66 //对该点染色 67 bmask[v]=1; 68 if(cy[v]!=-1&&dy[v]==dis) 69 { 70 continue; 71 } 72 if(cy[v]==-1||findpath(cy[v])) 73 { 74 cy[v]=u;cx[u]=v; 75 return 1; 76 } 77 } 78 } 79 return 0; 80 } 81 82 //得到最大匹配的数目 83 int MaxMatch() 84 { 85 int res=0; 86 memset(cx,-1,sizeof(cx)); 87 memset(cy,-1,sizeof(cy)); 88 while(searchpath()) 89 { 90 memset(bmask,0,sizeof(bmask)); 91 for(int i=1;i<=nx;i++) 92 { 93 if(cx[i]==-1) 94 { 95 res+=findpath(i); 96 } 97 } 98 } 99 return res; 100 } 101 102 103 int main() 104 { 105 int num; 106 scanf("%d",&num); 107 while(num--) 108 { 109 110 memset(bmap,0,sizeof(bmap)); 111 scanf("%d%d",&nx,&ny); 112 for(int i=1;i<=nx;i++) 113 { 114 int snum; 115 scanf("%d",&snum); 116 int u; 117 for(int j=1;j<=snum;j++) 118 { 119 scanf("%d",&u); 120 bmap[i][u]=1; 121 // bmap[u][i]=1; 122 } 123 } 124 // cout<<MaxMatch()<<endl; 125 if(MaxMatch()==nx) 126 { 127 printf("YES\n"); 128 } 129 else 130 { 131 printf("NO\n"); 132 } 133 } 134 //system("pause"); 135 return 0; 136 } 137 138 /* 139 140 4 141 1 3 142 1 3 4 143 2 144 145 146 */
二、
二分图的使用:
1、最小顶点覆盖:
在图中所有的点中找出来最小的点集合,使得图中的每一条边的两个顶点至少 有一个在这个点集中
结论:最小顶点覆盖 == 最大匹配
证明:假设当前存在一条两个端点都不在最小顶点覆盖点集中,那么这么这条边一定可以增大最大匹配边集,与最大匹配矛盾。
2、最小路径覆盖:在图中找一个最小的边集合,使得图中的每一个点都可以在这个边集合的断点处找到。
结论:最小路径覆盖 == 顶点数 - 最大匹配
证明:因为一条边最多可以包含两个顶点,所以我们选边的时候让这样的边尽量 多,也就是说最大匹配的边集合中边的数目。剩下的点就 只能一个边连上一 个点到集合里。
注意:最大匹配得到的是边的个数,(2*最大匹配)才是点的个数。所以(顶点数 - 最大匹配)得到的是(最大匹配后剩余的点)和(最大匹 配的边)
3、最大独立集:在N个点中选出来一个最大点集合,使这个点集合中的任意两点之间都没有边。
结论:最大独立集 == 顶点数 - 最大匹配
证明:因为去掉最大匹配两端的顶点去掉以后,剩下的点肯定是独立集。我们再从每个匹配里面挑选出来一个点加入到独立集中,也是不会破 坏原有独立集的独立性的。


