P1052 过河

题目描述

在河上有一座独木桥，一只青蛙想沿着独木桥从河的一侧跳到另一侧。在桥上有一些石子，青蛙很讨厌踩在这些石子上。由于桥的长度和青蛙一次跳过的距离都是正整数，我们可以把独木桥上青蛙可能到达的点看成数轴上的一串整点：0,1,…,L0,1,…,L0,1,…,L（其中LLL是桥的长度）。坐标为000的点表示桥的起点，坐标为LLL的点表示桥的终点。青蛙从桥的起点开始，不停的向终点方向跳跃。一次跳跃的距离是SSS到TTT之间的任意正整数（包括S,TS,TS,T）。当青蛙跳到或跳过坐标为LLL的点时，就算青蛙已经跳出了独木桥。

题目给出独木桥的长度LLL，青蛙跳跃的距离范围S,TS,TS,T，桥上石子的位置。你的任务是确定青蛙要想过河，最少需要踩到的石子数。

输入输出格式

输入格式：

 

第一行有111个正整数L(1≤L≤109)L(1 \le L \le 10^9)L(1≤L≤109)，表示独木桥的长度。

第二行有333个正整数S,T,MS,T,MS,T,M，分别表示青蛙一次跳跃的最小距离，最大距离及桥上石子的个数，其中1≤S≤T≤101 \le S \le T \le 101≤S≤T≤10,1≤M≤1001 \le M \le 1001≤M≤100。

第三行有MMM个不同的正整数分别表示这MMM个石子在数轴上的位置（数据保证桥的起点和终点处没有石子）。所有相邻的整数之间用一个空格隔开。

 

输出格式：

 

一个整数，表示青蛙过河最少需要踩到的石子数。

 

输入输出样例

输入样例#1： 复制 
10
2 3 5
2 3 5 6 7
输出样例#1： 复制 
2

说明

对于30%的数据，L≤10000L \le 10000L≤10000；

对于全部的数据，L≤109L \le 10^9L≤109。

2005提高组第二题

题解：

这道题要注意他不一定必须走到石头上，还可以走在没有石头的坐标上

 

之后这道题的dp方程很好推出来

该点为石头： dp[i]=min(dp[i],dp[i−j]+1)(s≤j≤t)dp[i] = min(dp[i],dp[i-j] +1)(s\leq j\leq t)dp[i]=min(dp[i],dp[i−j]+1)(s≤j≤t)

该点不为石头： dp[i]=min(dp[i],dp[i−j])(s≤j≤t)dp[i] = min(dp[i],dp[i-j])(s\leq j\leq t)dp[i]=min(dp[i],dp[i−j])(s≤j≤t)

但是看题目给出的数据1e9，就知道肯定要压缩路径

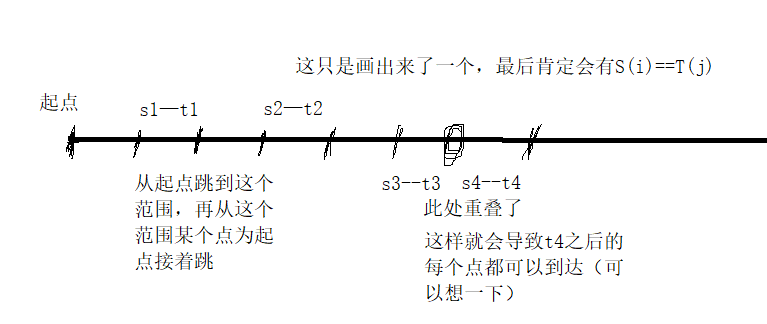
所以如果两个相邻的石头之间的距离大于lcm(s,t)，那么可以把他们的距离调成lcm(s,t)（lcm(s,t)是s和t的最小公倍数，这个点s和t都可以到达）

这个样子不就完成了路径压缩（缩点成功）

 

还要注意，这个输入的m个点还要对他排序（没有排序会RE）

 

代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 using namespace std;
 6 const int maxn=105*105;
 7 const int INF=0x3f3f3f3f;
 8 int stone[105],a[105],dp[maxn];
 9 bool vis[maxn];
10 int main()
11 {
12     int l,s,t,m;
13     scanf("%d",&l);
14     scanf("%d%d%d",&s,&t,&m);
15     int temp=s*t;
16     for(int i=1;i<=m;++i)
17     {
18         scanf("%d",&stone[i]);
19     }
20     sort(stone+1,stone+1+m);
21     if(s==t)
22     {
23         int cnt=0;
24         for(int i=1;i<=m;++i)
25             if(stone[i]%s==0) ++cnt;
26         printf("%d\n",cnt);
27         return 0;
28     }
29     for(int i=1;i<=m;++i)
30     {
31         int distance=stone[i]-stone[i-1];
32         if(distance>=temp) distance=temp;
33         a[i]=a[i-1]+distance;
34         vis[a[i]]=1;
35     }
36     l=a[m]+temp;
37     memset(dp,INF,sizeof(dp));
38     dp[0]=0;
39     for(int i=1;i<=l;++i)
40     {
41         for(int j=0;j<i;++j)
42         {
43             if(i-j>=s && i-j<=t)
44             dp[i]=min(dp[i],dp[j]+vis[i]);
45         }
46     }
47     int ans=INF;
48     for(int i=a[m];i<=l;++i)
49     {
50         ans=min(ans,dp[i]);
51     }
52     printf("%d\n",ans);
53     return 0;
54 }
View Code

 

还有一种方法——传送门

[前方高能,请数学学科恐惧症患者尽快撤离!!]

posted @ 2019-07-18 09:20  kongbursi  阅读(144)  评论(0)  编辑  收藏  举报