UVA442 矩阵链乘 Matrix Chain Multiplication

 

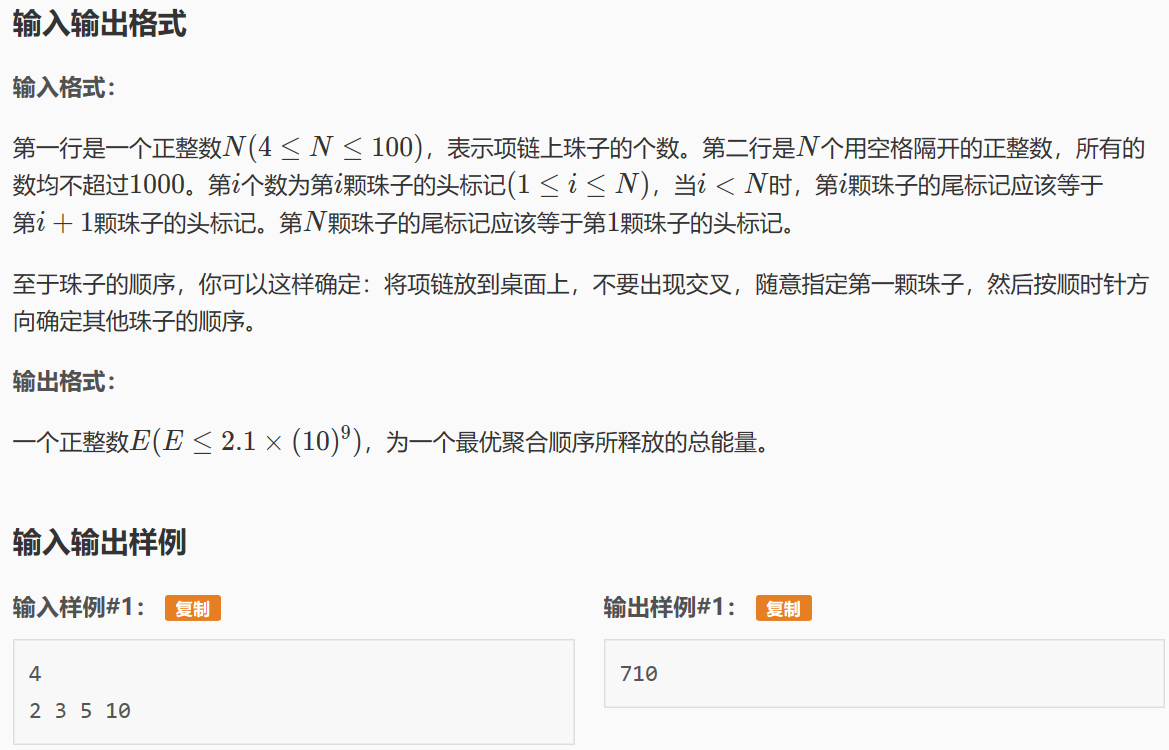
题意：

这道题也是在不改变原序列每个元素位置的前提下，看每个元素与他身边的两个元素那个先结合能得到最大的能量

题解：

很明显这是一道区间dp的题目，这道题要断环成链，这道题需要考虑在这个区间上某个元素先与那个元素结合更好，而如果我们采用了区间dp的模板，那么我们就在dp中不用考虑某个元素先于左右那个结合，因为区间dp的模板已经做到了这一点

i是起点，j是终点，k就是枚举父区间是由哪两个子区间合并而成的

dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+v[i]*v[k+1]*v[j+1])

 

 

但是最后的结果要在dp过程中取最大值，因为我们dp的最终长度是n，但是这个起点位置不是确定的，所以我们要用一个变量来取最大值

代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
const int maxn=2005;
const int INF=0x3f3f3f3f;
int dp[maxn][maxn],v[maxn],w[maxn];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&v[i]);
        v[n+i]=v[i];
    }
    v[2*n+1]=v[1];
    int maxx=0;
    for(int i=2;i<=n;++i)
    {
        for(int j=1;j+i<=2*n+1;++j)
        {
            int ends=j+i-1;
            for(int k=j;k<ends;++k)
            {
                dp[j][ends]=max(dp[j][ends],dp[j][k]+dp[k+1][ends]+v[j]*v[k+1]*v[ends+1]);
            }
            maxx=max(maxx,dp[j][ends]);
        }
    }
    printf("%d\n",maxx);
    return 0;
}