简单数学题（杭电）

已知

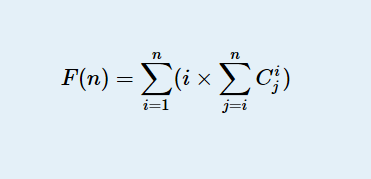
求 F(n) mod 1000000007

这一道题让我很绝望，刚开始感觉是简单模拟，一看数据是1e18我就知道不会这么简单

正解：本题要用到取模运算和快速幂，以及还要用用数学知识进行约分

数学化简是最难的：

 

 其中-sun是用sum-2sum得到的

1*2^0+2*2^1+3*2^2......

0+1*2^1+2*2^2......

错位相减（自己模拟一下）

代码如下：

#include<stdio.h>
#include<string.h>

typedef long long LL;

//LL q_mul(LL a, LL b, LL p) //快速乘法取模      这是为了防止在两个数做乘法运算的时候爆掉long long感觉和快速幂的原理差不多//

//例如32*5=32*（0101）=32*1*1+32*2*0+32*4*1+32*8*0；就是利用这个原理，是不是感觉和快速幂差不多
//{
//    LL ans = 0;
//    while (b)
//    {
//        if(b&1LL) ans=(ans+a)%p;
//        //or ans=(ans+(b%2*a)%p)%p;
//        a = (a +a) % p;
//        b >>= 1;
//    }
//    return ans;
//}
long long pow(long long x,long long y)//大家都知道（快速幂）
{
    if(!y) return 1;
    else
    {
        long long ans=1;
        while(y)
        {
            if(y&1LL)
            {
//            ans=q_mul(ans,x,1000000007);
//
                ans=((ans%1000000007)*(x%1000000007))%1000000007;
              //  printf("%lld\n",ans);
            }
            x=((x%1000000007)*(x%1000000007))%1000000007;//之前我没有在这里对x取余，导致x一直爆掉，下一次要记住了
            y>>=1;
        }
      //  printf("%lld\n",ans);
        return ans;
    }
}
int main()
{
    long long a,g;
    while(~scanf("%lld",&a))
    {
      //  g=q_mul((a-1),pow(2,a),1000000007);
        g=(((a-1)%1000000007*(pow(2,a)%1000000007))%1000000007+1)%1000000007;
        printf("%lld\n",g);
    }
    return 0;
}

其中还有一个知识就是：(a-b)%mod=(a%mod-b%mod)%mod=(a-b+mod)%mod;

这是为了防止a-b为负数