数据结构 浙大MOOC 笔记二 线性结构

线性表及其表现

第二章的内容是关于三种最基本的数据结构 结合《DDSA》第三章 表、栈和队列做一个总结

首先简单说明一下各个数据结构的特点：

数组：连续存储，遍历快且方便，长度固定，缺点是删除和添加数据需要移动(1,n)个数据，时间复杂度高

链表：离散存储，添加和删除方便，空间和时间消耗大，双向链表比单向的灵活，但是空间耗费也更大

Hash表：数据离散存储，利用hash 算法决定存储位置，遍历比较麻烦。 

二叉树： 一般的查找遍历，有深度优先和广度优先两种，遍历分前序、中序、后序遍历，效率都差不多。但是如果数据经过排序，则二叉树查找效率还是不错的。

图： 表示物件与物件之间的关系的数学对象，常用遍历方式为深度优先遍历和广度优先遍历，这两种遍历方式对有向图和无向图都适用，但是遍历查找不及前面任一种数据结构。

 

MOOC的课件首先由多项式的计算为例来引入了链表这一数据结构。多项式计算的关键在于存储关键数据 1.多项式项数n 2.各项系数a 3.指数i

 

方法1 数组存储结构直接表示

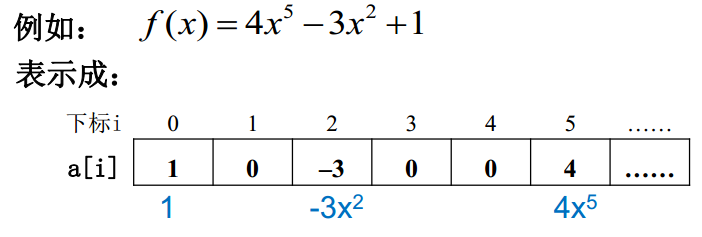
因为存在系数为0的项，所以会造成空间的浪费。改进得到方案2，顺序存储结构只表示非零项，

方法三：链表结构存储非零项

 

　　链表结构

 

 typedef 命令梳理 

typedef : you can use it to give a type, a new name.

 1 struct Books{
 2 
 3     char title[50];
 4     char author[50];
 5     char subject[100];
 6 };
 7 
 8 int main() {
 9     struct Books Book1, Book2;  //Declare Book1 , Book2 of type Books
10     
11     //book 1 specification
12     strcpy(Book1.title, "C Programming");
13     strcpy(Book1.author, "Nuha Ali");
14     strcpy(Book1.subject, "..");
15 
16 
17 typedef sturct Books{
18     char title[50];
19     char author[50];
20     char subject[100];
21 } Book;
22 
23 int main() {
24     Book book;  //只需要用Book 就可以表示 struct Books简写
25     strcpy(Book1.title, "C Programming");
26     strcpy(Book1.author, "Nuha Ali");
27     strcpy(Book1.subject, "..");
28 
29

 

 

“为了避免插入和删除的线性开销，我们需要允许表可以不连续存储，否则表的部分或全部需要整体移动。”
用数组来计算的话，优势在于
 
基本操作: MakeEmpty()  FindKth(int K, List L) Find(ElementType X, List L)
　　　　  Insert(ElementType X, int i, List L)  Delete(int i, List L)  Length(List L) 
 

 

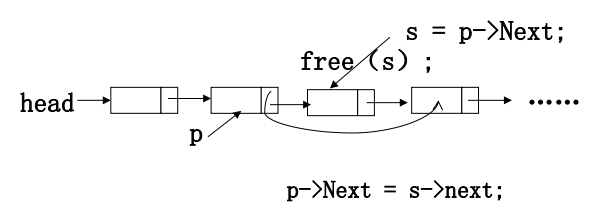
删除图例


 1 // Delete first occurrence of X from a list
 2 // Assume use of a header node
 3 
 4 void 
 5 Delete( ElementType X, List L )
 6 {
 7     Position P, TmpCell; //声明结构体指针
 8 
 9     P = FindPrevious (X, L);
10 
11     if( !IsLast( P, L ))
12     {
13             TmpCell = P->Next; //先存好P内含的指针，再删除P
14             P->Next = TmpCell->Next;
15             free(TmpCell);
16     }
17 }

删除例程 

插入：

先构造结点，P指向 n-1 的结点， 再修改带插入元素的指针

插入图例

 

 1 void Insert(ElementType X, List L, Position P)
 2 {
 3     Position TmpCell;
 4     
 5     TmpCell= malloc( sizeof (struct Node) );
 6     if( TmpCell == NULL)
 7         FatalError( "Out of space!!");
 8 
 9     TmpCell ->Element = X;
10     TmpCell ->Next = P->Next; //先修改插入元素的指针方向
11     P->Next = TmpCell;

 

 2.堆栈结构

导入： 计算机如何进行表达式求值？ 

两类存储对象 1.运算数 2.运算符号 

后缀表达式 与 中缀表达式 

后缀 abc * + de/ -  中缀 a+b*c - d / e

后缀表达式求值策略： 记住未参与运算的数， 遇到运算符号时判断运算符号级别决定运算顺序

6 2/ 3 - 4 2 * +　

６/２＝３　３３－ ＝０　４２× ＝８  ０＋８＝８　　

堆栈的抽象数据类型描述 

 CreatStack( int MaxSize) 创建堆栈

 IsFull(Stack S, int MaxSize) 判断堆栈是否满

 void Push (Stack S, ElementType item)  将item压入堆栈

 int IsEmpty (Stack S) 判断堆栈是否为空　　

 ElementType Pop(Stack S) 删除并返回栈顶元素

 

 

 

 

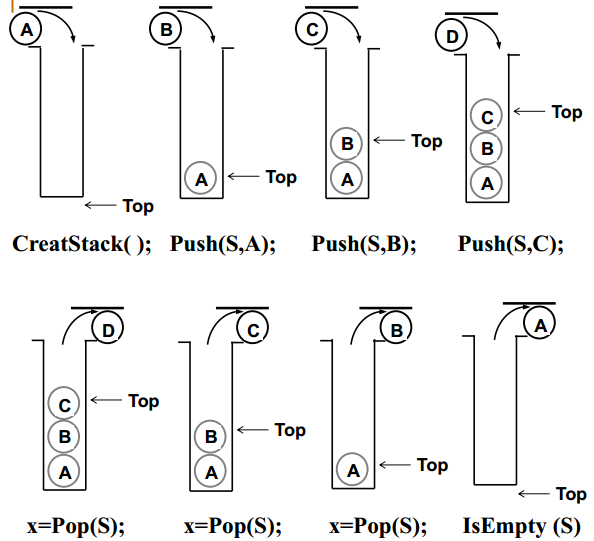
栈模型的链表实现与数组实现 

1 struct Node
2 {
3     ElementType Element;
4     PtrToNode Next;
5 };

链表实现基本的结构体组成

1 struct StackRecord
2 {
3     int Capacity;
4     int TopOfStack;
5     ElementType *Array;
6 };

数组实现的基本结构体组成

 

 

Push 的链表实现

 

Push 的数组实现

 

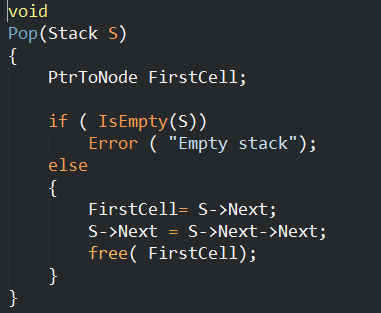
Pop的链表实现

 

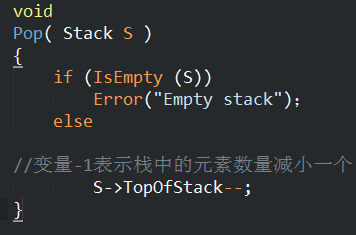
Pop的数组实现

栈的应用实例：

中缀表达式与后缀表达式的转换

扫描中缀表达式中个各个元素，运算数直接输出，运算符号存放在栈中，根据运算优先级确定Pop 和Push的先后顺序

后缀表达式的特点 遍历各元素，遇到运算符后计算与运算符最邻近的两个元素

优先级大的压栈，可以先出，左括号运算符优先级大于 * / 但是右括号返回至左括号的所有内容

 

 

2.3 队列

队列： 具有一定操作约束的线性表 插入和删除操作：只能在一端插入，而在另一端删除

抽象数据类型：

Queue CreatQueue(int MaxSize) ： 生成长度MaxSize 的空队列

int IsFullQ( Queue Q, int MaxSize):  判断队列Q是否已满

void AddQ( Queue Q, ElementType item): 将数据元素item 插入队列Q中

int IsEmptyQ( Queue Q): 判断队列Q是否为空

ElementType DeleteQ(Queue Q): 将队头数据元素从队列中删除并返回

 

 

 

front做删除操作 rear做插入操作   为空间的充分利用可以使用循环数组

 

潜在问题： 无法判定队列的状态是空 还是满

解决方案：1.使用额外标记 Size 或tag域 2.仅使用n-1个数组空间 

 

队列的删除图例

 

 

　

 

 

 

posted @ 2017-01-02 11:26  AugusKong  阅读(263)  评论(0)  编辑  收藏  举报