稀疏矩阵转置
稀疏矩阵转置
前置知识：稀疏矩阵用三元组的保存
一般来说，对于系数矩阵，我们使用三元组来存储。即就是将矩阵的所有非零元素的三元组存放在一个顺序表中，如图所示：
注意一个转置的前提：该顺序表是排好序的，即行优先，列其次。
这里的稀疏矩阵为静态分配空间，所以会有MAXSIZE+1个三元组，但实际上转置时遍历是按照len长度来遍历的
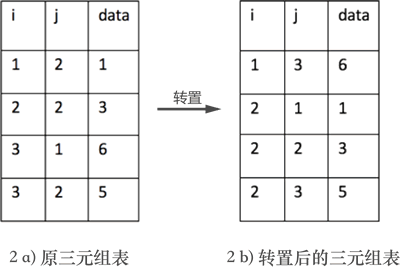
图 2a) 表示的是图 1 中转置之前矩阵的三元组表，2b) 表示的是图 1 中矩阵转置后对应的三元组表。
矩阵转置的实现过程需完成以下 3 步：
- 将矩阵的行数和列数互换；
- 将三元组表（存储矩阵）中的 i 列和 j 列互换，实现矩阵的转置；
- 以 j 列为序，重新排列三元组表中存储各三元组的先后顺序；
一、普通转置
实现思路是：
不断遍历存储矩阵的三元组表，每次都取出表中 j 列最小的那一个三元组，互换行标和列标的值，并按次序存储到一个新三元组表中，。
例如，将图 2a) 三元组表存储的矩阵进行转置的过程为：
- 新建一个三元组表（用于存储转置矩阵），并将原矩阵的行数和列数互换赋值给新三元组；
- 遍历三元组表，找到表中 j 列最小值 1 所在的三元组 (3,1,6)，然后将其行标和列标互换后添加到一个新的三元组表中，如图 3 所示：
-
继续遍历三元组表，找到表中 j 列次小值为 2 的三元组，分别为 (1,2,1)、(2,2,3) 和 (3,2,5)，根据找到它们的先后次序将各自的行标和列标互换后添加到新三元组表中，如图 4 所示：
注：因为文章要求开头提到了，转置的前提是"该顺序表是排好序的，即行优先，列其次。"，所以按照遍历到他们的先后顺序(在原矩阵中data下标按行递增查找)放入新矩阵后，他们按照j也是有序的(此时i相同)。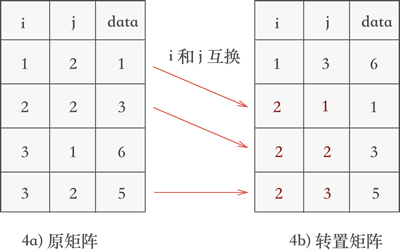
对比图 4 和图 2b) 可以看到，矩阵被成功地转置。
基于上面描述的代码有：
代码
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<stdbool.h>
#define MAXSIZE 1000
#define number 10
//定义三元组
typedef struct{
int row;//第几行
int col;//第几列
int val;//存储的数值
} Triple;
//定义稀疏矩阵
typedef struct{
Triple data[MAXSIZE];
int m, n, len; //稀疏矩阵的行、列、非零元素的个数
} TSMatrix;
void TransMatrix(TSMatrix *, TSMatrix *);
int main(void){
TSMatrix M;
M.m = 4;
M.n = 3;
M.len = 4;
M.data[1].row = 1;
M.data[1].col = 2;
M.data[1].val = 1;
M.data[2].row = 2;
M.data[2].col = 2;
M.data[2].val = 3;
M.data[3].row = 3;
M.data[3].col = 1;
M.data[3].val = 6;
M.data[4].row = 3;
M.data[4].col = 2;
M.data[4].val = 5;
TSMatrix T;
for (int k = 0; k < number; k++) {
T.data[k].row = 0;
T.data[k].col = 0;
T.data[k].val = 0;
}
TransMatrix(&M, &T);
for (int i = 1; i <= T.len; i++) {
printf("(%d,%d,%d)\n", T.data[i].row, T.data[i].col, T.data[i].val);
}
return 0;
}
//稀疏矩阵的转置,A为装置前矩阵，B为转置后矩阵
void TransMatrix(TSMatrix *A, TSMatrix *B){
B->len = A->len; //复制A中非零元素个数至B
B->m = A->n; //将A的行数与列数与B的交换
B->n = A->m;
int q = 1; //辅助计数器，记录转置后的三元组(下一个插入)元素下标值，
//注意：这里A.data[]数组下标从1开始，三元组下标从0开始
if(A){
for (int col = 0; col < A->n; col++){ //按照列优先来遍历矩阵A(因为要先从列最小开始存放至新矩阵中)
for (int p = 1; p <= A->len; p++){ //按照下标递增次序遍历三元组，寻找列下标一致的
if(col==(A->data[p].col)){ //找到，则交换该三元组的行列下标放至新矩阵中
B->data[q].col = A->data[p].row;
B->data[q].row = A->data[p].col;
B->data[q].val = A->data[p].val;
q++;
}
}
}
}
}
运行结果见 图2a) 2b)
二、快速转置
思想：按稀疏矩阵的三元组(source)次序转置，转置结果放入新稀疏矩阵的三元组(dest)中的恰当位置。
- 关键：
- 预先确定source中每一列第一个非零元在dest中位置。
- 为确定这些位置，转置前应先求得source的每一列中非零元个数
- cpos[col] 的计算方法：
初始：cpos[1]=1
其他：cpos[col]=cpos[col-1]+num[col-1] (2<=col<=M.nu)
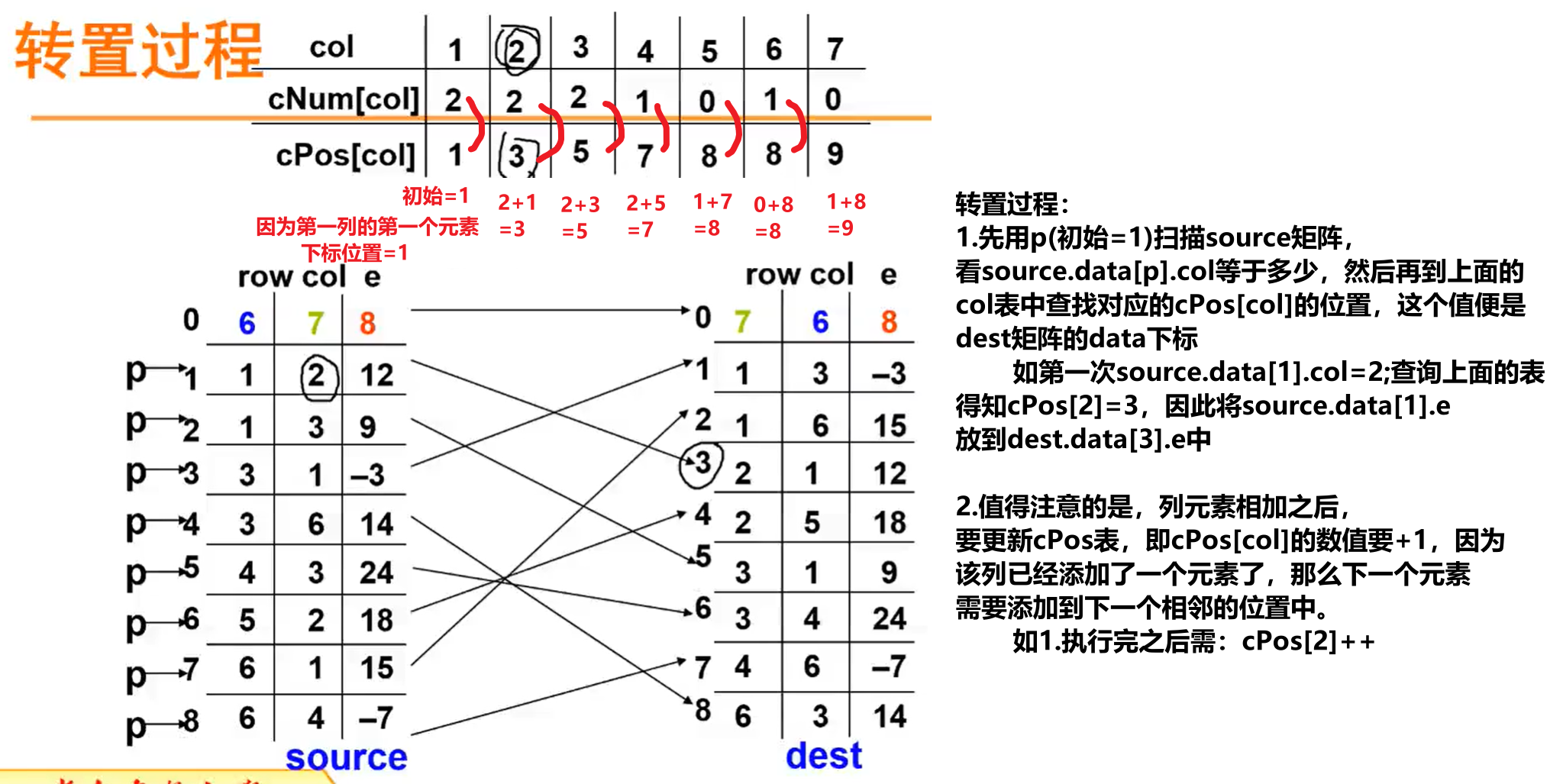
代码
//用三元组表示(顺序存储)的稀疏矩阵的两种转置方法转置
#include<stdio.h>
#include<malloc.h>
#include<stdlib.h>
#include<stdbool.h>
#define MAXSIZE 1000
#define number 10
//定义三元组
typedef struct{
int row;//第几行
int col;//第几列
int val;//存储的数值
} Triple;
//定义稀疏矩阵
typedef struct{
Triple data[MAXSIZE];
int m, n, len; //稀疏矩阵的行、列、非零元素的个数
} TSMatrix;
void Transpose(TSMatrix *, TSMatrix *);
int main(void){
TSMatrix M;
M.m = 4;
M.n = 3;
M.len = 4;
M.data[1].row = 1;
M.data[1].col = 2;
M.data[1].val = 1;
M.data[2].row = 2;
M.data[2].col = 2;
M.data[2].val = 3;
M.data[3].row = 3;
M.data[3].col = 1;
M.data[3].val = 6;
M.data[4].row = 3;
M.data[4].col = 2;
M.data[4].val = 5;
TSMatrix T;
for (int k = 0; k < number; k++) {
T.data[k].row = 0;
T.data[k].col = 0;
T.data[k].val = 0;
}
// TransMatrix(&M, &T);
Transpose(&M, &T);
for (int i = 1; i <= T.len; i++) {
printf("(%d,%d,%d)\n", T.data[i].row, T.data[i].col, T.data[i].val);
}
return 0;
}
void Transpose(TSMatrix *source, TSMatrix *dest){
//采用三元组顺序表存储表示，求稀疏矩阵M的转置矩阵T
int cNum[MAXSIZE] = {0};
int sPos[MAXSIZE] = {0};
dest->m = source->n;
dest->n = source->m;
dest->len = source->len; //将M的行数赋值给T的列数，将M的列数赋值给T的行数，非零元素总数也赋值过去
for (int i=0; i<source->n; i++)
cNum[i] = 0; //初始化假设原三元组每一列元素出现次数都为0
for (int i = 1; i <= source->len;i++)
++cNum[source->data[i].col]; //枚举每一个非0元素， M.data[t].j 为其相应的列
sPos[1]=1; //求第 col列中第一个非零元在T.data中的序号
for (int i=2; i<source->n; i++) //存储source第col列中第一个非零元素在dest的位置
sPos[i] = sPos[i - 1] + cNum[i - 1];
for (int p = 1; p <= source->len; ++p)
{ //枚举所有的三元组
int col = source->data[p].col; //将第i个三元组的列数赋值给col
int q=sPos[col];
/*取出spot数组中spot[col]的值，注意，这里很重要：因为在顺序表中，所有的行元素的大小已经是依次排好的，
所以我们遍历到的这个三元组时，当其与其后面的拥有相同列元素的三元组进行比较的时候，它一定是最小的，
所以应该放在前面时，所以我们取完这个值之后，将spot[col]的值+1，即可在下面的遍历中搜索到与之邻近的
值，正好下标已经+1，直接添加上去即可*/
dest->data[q].row=source->data[p].col;
dest->data[q].col=source->data[p].row;
dest->data[q].val = source->data[p].val; //赋值操作
++sPos[col]; //下标记录+1
}
}
