从斐波那契到矩阵快速幂

说起斐波那契数列大家应该都很熟悉，一个简单的递推公式

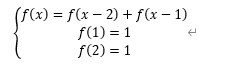
大家应该很容易想出形如这样的代码。

int fib(int x) {
    if (x == 1 || x == 2)return 1;
    return fib(x - 2) + fib(x - 1);
}

一个经典的递归方法。

但这个代码的时间复杂度很差，计算到x=40的情况就有点勉强了，因为他其中有太多次重复的计算了。

比如我们输入x=10，需要计算f(8)与f(9),计算f(9),需要f(8)和f(7)，这里f(8)就重复的计算了两次，在这重复的递归下去重复的计算会越来越多，导致速度缓慢，甚至因为递归次数过多导致栈内存溢出(进入函数后会把上一个函数的一系列信息先暂存在栈中，如果递归次数过多，导致栈的内存不够用，就会导致错误)。

既然是因为重复计算导致高的时间复杂，我们可以记录已经计算过的那部分，下次碰到就直接使用，这就是记忆化搜索。

对上面的函数稍加修改可得

//记录第fb[x]表示第x个斐波那契数列
int fb[100] = {0,1,1};
//为fb数组前3个值赋值
//同fb[0]=0,fb[1]=1,fb[2]=1;

int fib(int x) {
    if (fb[x])return fb[x];//fb[x]非0，说明该值已经计算过，直接返回
    //记忆计算过的值
    fb[x - 1] = fib(x - 1);
    fb[x - 2] = fib(x - 2);
    return fb[x - 1] + fb[x - 2];
}

稍微测试以上的代码，我们发现速度非常的快了，但发现输入稍大点的数就会输出负数，这是因为斐波那契数列往后越来越大，导致超出int，甚至long long的表实范围。C++没有java或者python 那样自带大数计算，如果需要表现斐波那契数列的后面部分的数值就需要手动写大数计算，由于斐波那契数列的计算性质我们只要实现大数加法，这倒是不是很麻烦。

大数计算简单的讲就是，使用数组来模拟数字，数组中每一个元素表示数字的一个位。那样大数加法就是，将每一位相加并进位，就如我们手算加分那样，乘法同样是我们从小学的那种乘法竖式计算。

但一般来说不会要我们输出斐波那契数列的大数，一般来说是对斐波那契数列取模。

稍加修改我们就得出取模的函数

const int mod = 1e9;
int fb[100005] = { 0,1,1 };
int fib(int x) {
    if (fb[x])return fb[x];
    fb[x - 1] = fib(x - 1);
    fb[x - 2] = fib(x - 2);
    return (fb[x - 1] + fb[x - 2])%mod;
}

但我们发现输入稍大的数就会弹出错误，这就是上文中提到的栈溢出，次数过多的递归会导致栈溢出，解决方法是，手动模拟递归过程，将数据储存在堆中，或者，换种方式，不使用递归计算。模拟递归有兴趣的可以自行了解，在这就不多展开了。

我们要换种方法，分析递归的方法我们发现，递归是一种自上而下再从下返回计算的算法。上文的递归在自上而下中是没有进行计算的，只有在自下而上的返回时才有具体的值计算，并且在递归中从1~n-1，的斐波那契数列都计算过一遍，那我们能不能直接自下而上的进行计算，显然可以，我们直接从头开始循环，一步一步的递推到结果。

const int mod = 1e9;
int fb[100005] = { 0,1,1 };
int k = 2;
int fib(int x) {
    while (x > k) fb[++k] = (fb[k - 2] + fb[k - 1])%mod;
    return fb[x];
}

观察递推公式我们发现，如果没有多次查询，那我们一次只要储存2个数据就可以推出下一个斐波那契数，所以我们还有以下这种写法

const int mod = 1e9;
int fib(int x) {
    int f[] = { 0,1 };
    int tmp;
    while (--x) {
        tmp = f[1];
        f[1] = (f[1]+f[0])%mod;
        f[0] = tmp;
    }
    return f[1];
}

以上的这几种算法的时间复杂度已经是O（n）级别了，属于非常低的一种程度了。

但其实可以进一步优化，使时间复杂度变为O（logn）,.斐波那契数列递推出下一个状态只需要前两个数就能推出，也就是说我们有f[]={a,b}这两个相邻的斐波那契数，我们需要的是将{a，b}变为{b，a+b}然后重复该操作，也就是上一个代码的操作。这时就用到一个比较神奇的操作了，我们把数组f[]看成一个2*1的矩阵[a,b],[a,b]到[b，a+b]的变化我们可以用一个矩阵乘法来表示，即[a,b]*A=[b，a+b]，显然当A=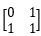时，等式成立。

即[a,b]*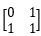=[a*0+b，a+b]= [b，a+b]。

这时我们用数学的方式把一种具体的变化抽象成数学符号。

我们不妨设F(n)=[f(n),f(n+1)]称它为状态矩阵(f(n)为第n个斐波那契数列)，称A为转移矩阵。这时有

F(n+1) = F(n)*A;

即[f(n+1),f(n+2)] = [f(n+1),f(n)+f(n+1)] =[f(n),f(n+1)]*A

根据矩阵乘法的特性易知

F(n)=F(1)*A^(n-1);

这时有的人可能会疑惑了，经行了这么多的步骤大费周章的把问题数学化，但最后还是要一步一步的去进行矩阵乘法，复杂度甚至比之前的还差。

但是先不要着急，我们这么大费周章其实是为了这个A，这个不包含可变量的A的连乘，我们有一些方法可以对这个连乘进行优化，也就是对A的次方进行优化。

我们先摒弃A的矩阵属性，我们把A先化简成一个普通的数。

这时我们得到一个新的问题，x^y 该如何计算。

大家应该很轻松的可以写出形如这样的代码：

int pow(int x, int y) {
    int ans = 1;
    while (y--)ans *= x;
    return ans;
}

代码复杂度是O（y），我们的目标是优化它，上面代码的流程是进行累乘，但如果y很大时，一步步累乘繁琐而缓慢，如果多个多个乘应该会快很多，比如a^7,我们直接写成a^4+a^2+a 就只要递推3次就可以得到答案，a^4 可以由a^2自乘得到，a^2也可以由a自乘得到，自乘在代码中可以使a指数性上升，可以说非常快了，如果运用自乘我们可以将y分割成2^n 的和，如6 分割成 2^2+2^1+2^0。这就与二进制表示不谋而合。我们也可以很轻松的用c++/c 中的二进制操作来实现代码。

int pow(int x, int y) {
    int ans = 1;
    while (y) {
        if (y & 1)ans *= x;
        x *= x;
        y >>= 1;
    }
    return ans;
}

代码的流程，例如：

输入a 和23. 23的二进制码是 10111

先判断y是否是0，非0进入循环。                                   

取y的最低为判断是否是1，是1就ans乘上x ，10111 最低位是1，所以ans*=x，此时ans=a

然后 a自乘 x=a^2

将y右移一位，y=1011

同样先判断y是否是0，非0进入循环，取y的最低为判断是否是1，是1就ans乘上x 1011最低位是1，所以ans*=x，此时ans=a+a^2

…

直到y=0 跳出循环这时 ans=a+a^2+a^4+a^16=a^23

这就是快速幂，这时复杂度已经达到O（logn）已经是非常快的速度了。按上面的这种方法，类似的我们还可以推出10进制的快速幂，这里就不做展开了。

 

让我们回到上面的矩阵幂运算，运用同样的方法对矩阵使用快速幂，我们就可以得到O（m^3 logn）复杂度 (m是转移矩阵的大小，m^3 也就是进行一次矩阵乘法的复杂度，)的斐波那契数列算法了。

终于，在讲这么多的前置知识后我们回到我们的正题，矩阵快速幂算法

与上面的快速幂几乎一样，只不过乘法换成了矩阵乘法

typedef long long ll;
const ll mod = 1e9 + 7;
const int N = 2;//矩阵大小
int c[N][N];
//状态转移
void mul(ll f[N], ll a[N][N]) {
    ll c[N];
    memset(c, 0, sizeof(c));
    for (int j = 0; j < N; j++)
        for (int k = 0; k < N; k++)
            c[j] = (c[j] + f[k] * a[k][j]) % mod;
    memcpy(f, c, sizeof(c));
}
//自乘
void mulself(ll a[N][N]) {
    ll c[N][N];
    memset(c, 0, sizeof(c));
    for (int i = 0; i < N; i++)
        for (int j = 0; j < N; j++)
            for (int k = 0; k < N; k++)
                c[i][j] = (c[i][j] + (a[i][k] * a[k][j])) % mod;
    memcpy(a, c, sizeof(c));
}

//f是状态矩阵，a是转移矩阵，n是指数
ll* pow(ll f[N], ll a[N][N],ll n) {

    while (n) {
        if (n & 1)mul(f, a);
        mulself(a);
        n >>= 1;
    }
    return f;
}

例题：

基础

https://vjudge.net/problem/HRBUST-1115   斐波那契数（取模）

https://vjudge.net/problem/HRBUST-2170   斐波那契数（大数）

https://vjudge.net/problem/POJ-3070  Fibonacci（矩阵快速幂）

提高：

https://vjudge.net/problem/HDU-5950     Recursive sequence （acm亚洲赛真题 ，矩阵快速幂运用）

https://www.cnblogs.com/komet/p/13770633.html（题解）