信号与系统学习笔记 五--离散时间信号与系统频域分析

周期信号的离散时间傅里叶级数(DFS)

• 回顾：连续时间信号频域分析思路
  
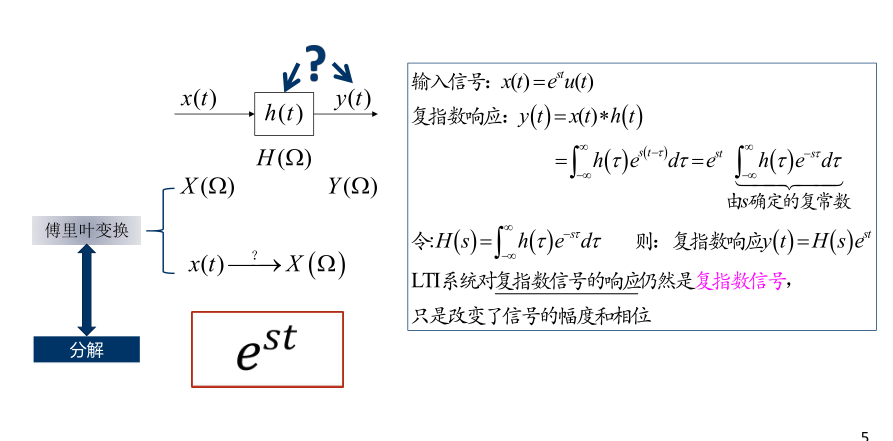
• 离散时间LTI系统特征函数
  
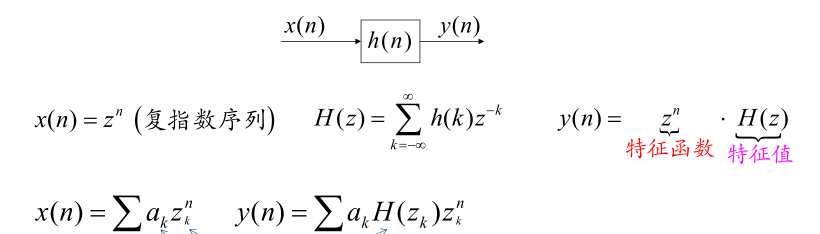
• 周期信号\(x(n)=x(n+N)\)
• 离散复指数信号：
  \(e^{jwn}=e^{jw(n+N)}\) (满足\(\frac {w}{2\pi}=\frac{m}{N})\)
  基波周期为N的周期信号：\(e^{j\frac{2\pi}{N}n}\)
  把所有的周期为N的离散时间周期性复指数信号组合起来，构成信号集： $ \phi_k(n)$= \(e^{j\frac{2\pi}{N}kn}\) \(k=0,\pm1,\pm2，\cdots\)
  注意：与连续时间信号不同，\(\phi_k(n)\)中只有N个序号相连的序列是相互独立的
  将\(\phi_k(n)\)的所有独立的N个信号线性组合起来，它们的组合一定也是以N为周期的离散时间信号，因此，可以用成谐波关系的复指数信号的线性组合表示离散时间周期信号，这就是DFS。

DFS

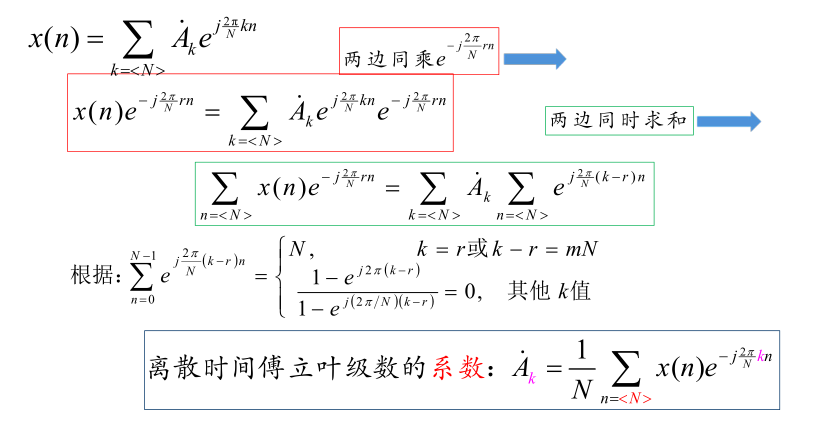
• 离散时间傅里叶级数系数
  1） 是以N为周期的周期信号，周期信号频谱也是周期的
  2）\(\dot{A_k}\)的实部是关于k的偶函数，虚部是关于k的虚函数；模是偶函数，相角是奇函数
  3）主值周期：k=[0,N-1]
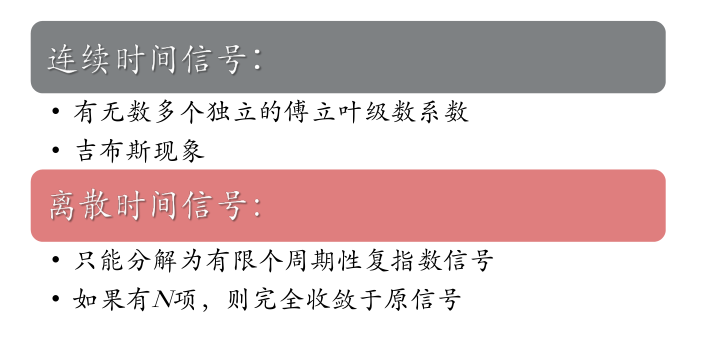
  4）不存在收敛问题
• 比较
  

周期性矩形脉冲序列的频谱

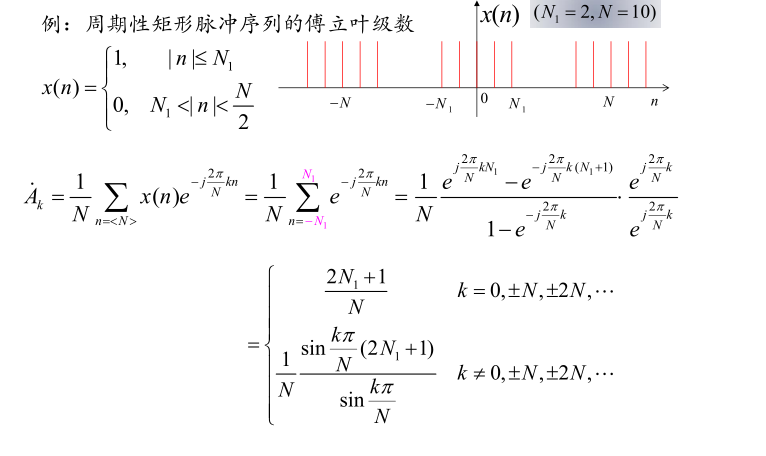
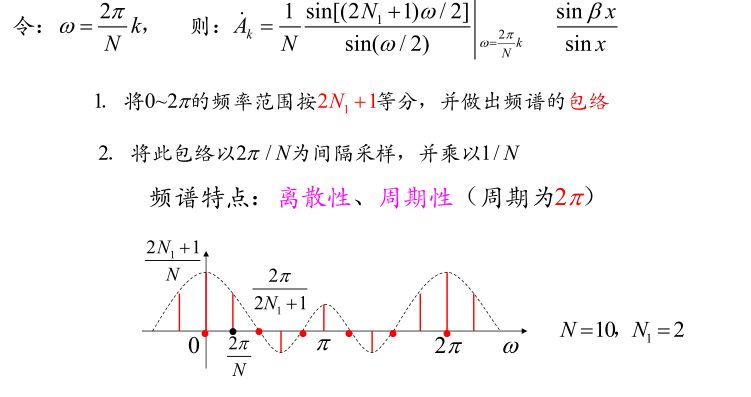
• \(N\)不变，\(N_1\)增大
  
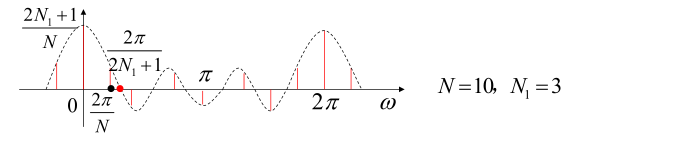
  脉冲宽度增大，频谱包络主瓣的宽度变窄，幅度增加，周期不变，谱线间隔不变
• \(N\)增大，\(N_1\)不变
  
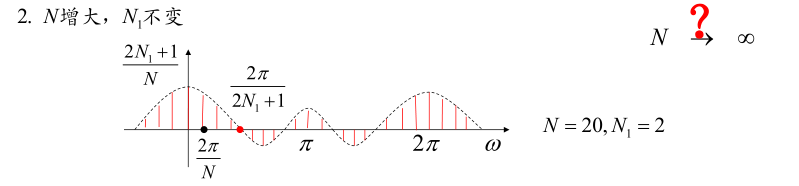
  脉冲宽度不变，频谱包络形状不变。周期增大，频谱幅度减小，谱线间隔减小

离散时间非周期信号傅里叶变换（DTFT）

常用序列的傅里叶变换

单边指数序列：\(x(n)=a^nu(n),\vert a\vert<1\)

双边指数序列：\(x(n)=a^{\vert n\vert},\vert a\vert<1\)

单位脉冲序列：\(x(n)=\delta(n)\)

常数序列：\(x(n)=1\)

离散符号函数序列：\(sgn(n)\)

单位阶跃函数序列：\(x(n)=u(n)\)

矩形脉冲信号

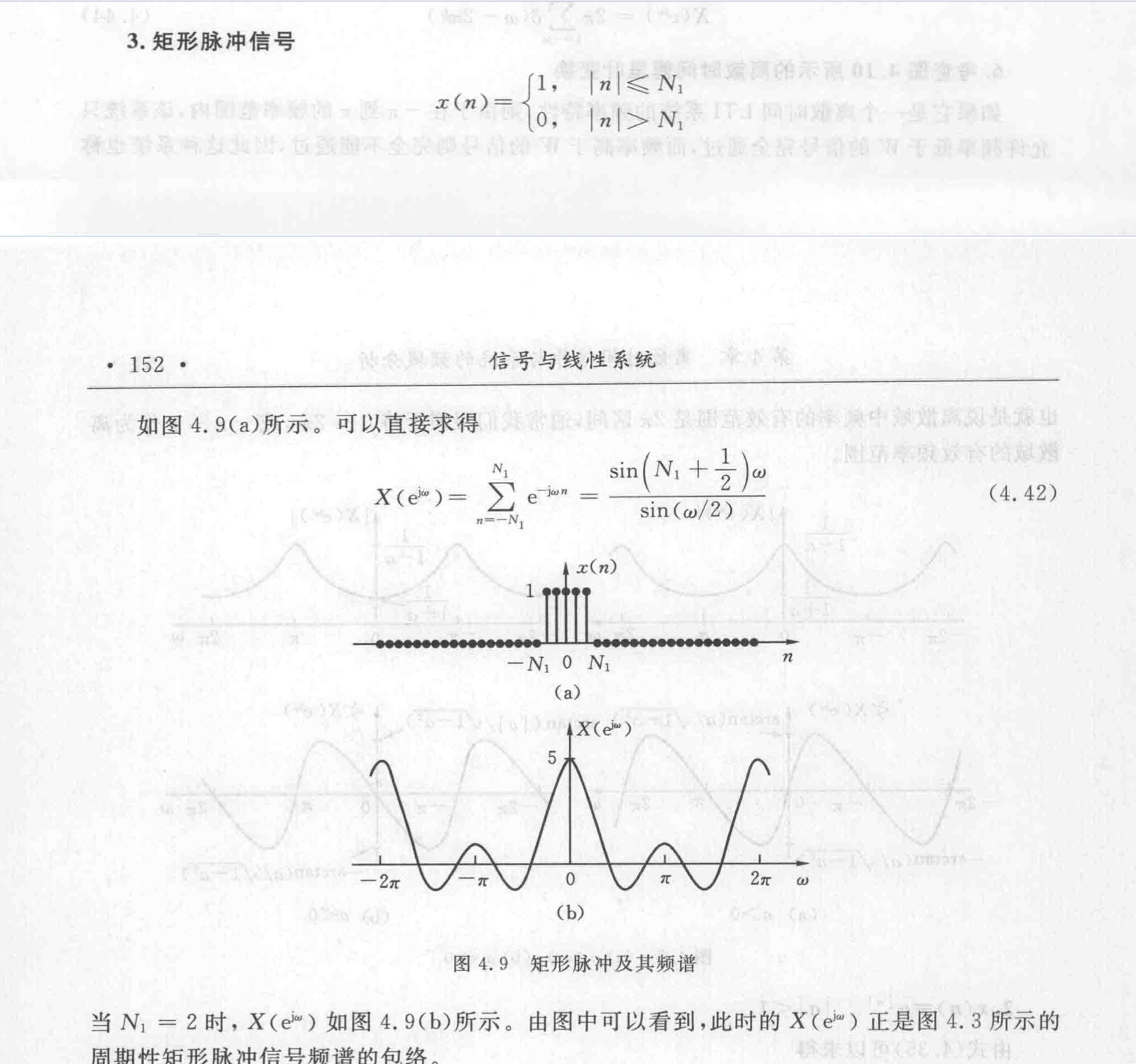
离散时间周期信号傅里叶变换

离散时间傅里叶变换性质

周期性

线性性质

共轭对称性

时延特性

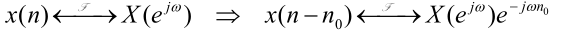
频移特性

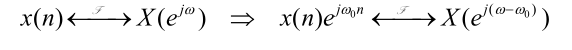
时域和频域的尺度变换

时域差分与求和

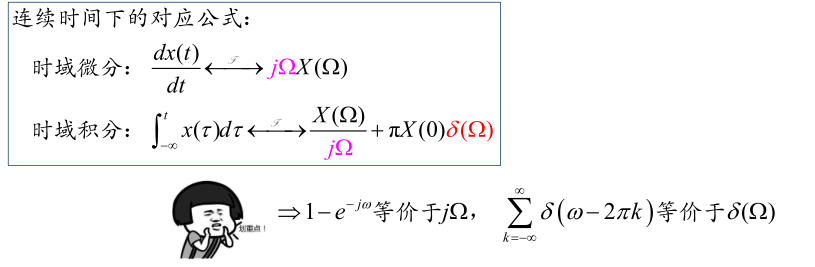
频移微分特性

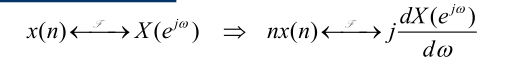
时移卷积特性（频移分析理论基础）

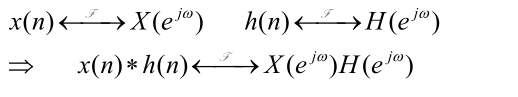
频移卷积特性（调制理论基础）

对偶特性

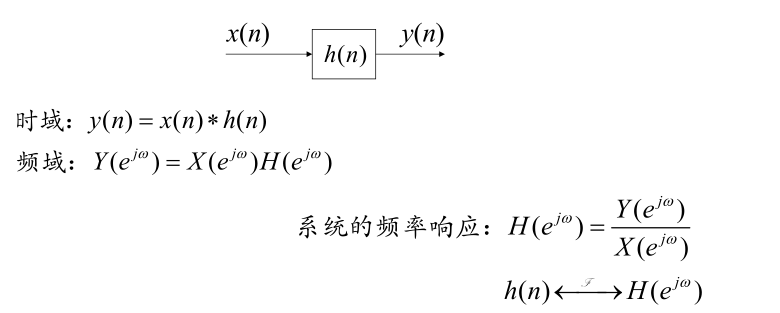
离散时间系统频域分析

• 频率响应