平面或空间中任意点的旋转
平面或空间中任意点的旋转
自己琢磨出来的。若有错误请指出。谢谢！
1. 旋转2D
假设平面上有一个点\(P(x, y)\)，旋转任意角度\(\beta\)，求旋转后的点\(P'(x',y')\)。
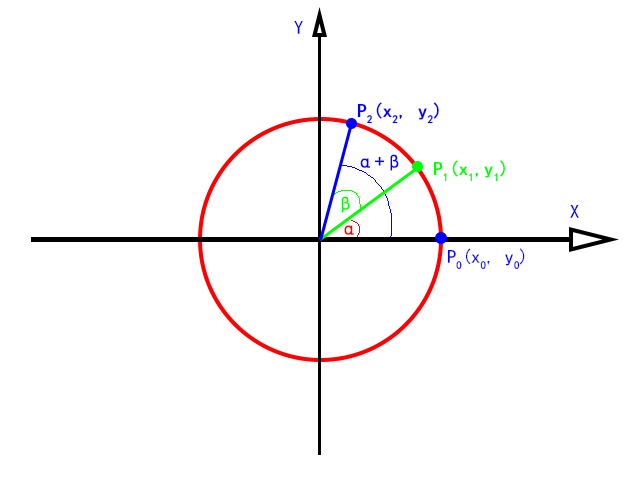
设平面坐标系上有一个半径为\(r\)的圆，圆心位于原点\(O\)。圆与\(x\)轴正坐标的交点为\(P_0(x_0, y_0)\)。
\[P_0 = \begin{cases}
x_0 = r\\
y_0 = 0\\
\end{cases}
\]
将点\(P_0\)旋转任意角度\(\alpha\)弧度得任意点\(P_1(x_1, y_1)\)，那么点\(P_1(x_1, y_1)\)的坐标该怎么通过计算获得？
\[P_1=\begin{cases}
x_1 = r \times cos(\alpha)\\
y_1 = r \times sin(\alpha)\\
\end{cases}
\]
现在将另一任意点\(P_2(x_2, y_2)\)相对于点\(P_1(x_1, y_1)\)旋转任意角度\(\beta\)，那么点\(P_2(x_2, y_2)\)的坐标该怎么通过计算获得？
\[P_2 = \begin{cases}
x_2 = r \times cos(\alpha+\beta)\\
y_2 = r \times sin(\alpha+\beta)\\
\end{cases}
\]
使用三角函数的和角公式把点\(P_2\)的坐标公式展开得：
\[P_2=\begin{cases}
x_2=r \times cos(\alpha+\beta) = r \times cos\alpha \times cos\beta - r \times sin\alpha \times sin\beta\\
y_2=r \times sin(\alpha+\beta) = r \times sin\alpha \times cos\beta + r \times cos\alpha \times sin\beta
\end{cases}
\]
把\(P_1\)得坐标带入上面\(P_2\)的坐标展开式，则有：
\[P_2=\begin{cases}
x_2=x_1 \times cos\beta - y_1 \times sin\beta\\
y_2=y_1 \times cos\beta + x_1 \times sin\beta\\
\end{cases}
\]
总结：对于平面上任意点\(P(x, y)\)，旋转任意角度\(\beta\)后，得到的点\(P'(x', y')\)为：
\[P'=\begin{cases}
x'=x \times cos\beta - y \times sin\beta\\
y'=y \times cos\beta + x \times sin\beta\\
\end{cases}
\]
三角函数和差公式
\[sin(\alpha+\beta)=sin\alpha \cdot cos\beta + cos\alpha \cdot sin\beta\\ sin(\alpha-\beta)=sin\alpha \cdot cos\beta - cos\alpha \cdot sin\beta\\ cos(\alpha+\beta)=cos\alpha \cdot cos\beta - sin\alpha \cdot sin\beta\\ cos(\alpha-\beta)=cos\alpha \cdot cos\beta + sin\alpha \cdot sin\beta\\ \]
2. 旋转3D
假设平面上有一个点\(P(x, y, z)\)，绕\(x\)轴、\(y\)轴和\(z\)轴相对于原点旋转任意角度\(\alpha\)、\(β\)和\(\gamma\)，求旋转后的点\(P'(x',y', z')\)。
按照类似于2D的情况来考虑此问题。该问题可以分解为分别在\(yz\)平面，\(xz\)平面和\(xy\)平面内相对于原点旋转。那么，有以下结论：
在\(yz\)平面内绕\(x\)轴相对于原点旋转\(\alpha\)角度旋转：
\[\begin{align}
&x'=x\\
&y'=y \times cos\alpha-z \times sin\alpha\\
&z'=z \times cos\alpha+z \times sin\alpha\\
\end{align}
\]
在\(xz\)平面内绕\(y\)轴相对于原点旋转\(\beta\)角度旋转：
\[\begin{align}
&x'=x \times cos\beta-z \times sin\beta\\
&y'=y \\
&z'=z \times cos\beta+x \times sin\beta\\
\end{align}
\]
在\(xy\)平面内绕\(z\)轴相对于原点旋转\(\gamma\)角度旋转：
\[\begin{align}
&x'=x \times cos\gamma-y \times sin\gamma\\
&y'=y \times cos\gamma+x \times sin\gamma\\
&z'=z\\
\end{align}
\]
注：绕\(z\)轴旋转，理解为点\(P\)在\(xy\)平面内的投影，并绕原点旋转。其余的情况类似。
3. 代码
这里使用Python语言来编写上面两种旋转的代码，如下：
import math
def rotate_2d(x: int | float,
y: int | float,
rad: int | float) -> (float, float):
"""
Rotate a point around orientation at any given radian.
:param x: X scale of point.
:param y: Y scale of point.
:param rad: Radian value to be rotated.
:return: A new point has been rotated by rad radian.
:raise: None.
"""
rad = float(rad)
r_x: float = (x * math.cos(rad)) - (y * math.sin(rad))
r_y: float = (y * math.cos(rad)) + (x * math.sin(rad))
return r_x, r_y
def rotate_3d(x: int | float,
y: int | float,
z: int | float,
ax: float,
ay: float,
az: float) -> (float, float, float):
"""
Rotate a point in 3d space around orientation at any given radian.
:param x: X scale of point.
:param y: Y scale of point.
:param z: Z scale of point.
:param ax: Radian value to be rotated around orientation x.
:param ay: Radian value to be rotated around orientation y.
:param az: Radian value to be rotated around orientation z.
:return: A new point has been rotated by rad radian.
:raise: None.
"""
ax = float(ax)
ay = float(ay)
az = float(az)
# rotate around axis x
r_x = x
r_y = y * math.cos(ax) - z * math.sin(ax)
r_z = z * math.cos(ax) + y * math.sin(ax)
x, y, z = r_x, r_y, r_z
# rotate around axis y
r_y = y
r_x = x * math.cos(ay) - z * math.sin(ay)
r_z = z * math.cos(ay) + x * math.sin(ay)
x, y, z = r_x, r_y, r_z
# rotate around axis z
r_z = z
r_x = x * math.cos(az) - y * math.sin(az)
r_y = y * math.cos(az) + x * math.sin(az)
return r_x, r_y, r_z
def radian(degree: int | float):
"""
Convert radian value in to radian value.
:param degree: Degree value to be converted.
:return: Radian value.
:raise: None.
"""
return degree * math.pi / 180.0
if __name__ == "__main__":
def main():
x = 1.0
y = 0.0
for i in range(360+1):
p = rotate_2d(x, y, radian(i))
print("{:>3d} degree, ".format(i), '(x: {:+.3f}, y:{:+.3f})'.format(*p))
return
main()
参考资料：
