计算机基础知识之原码、补码、反码和移码
补数的概念
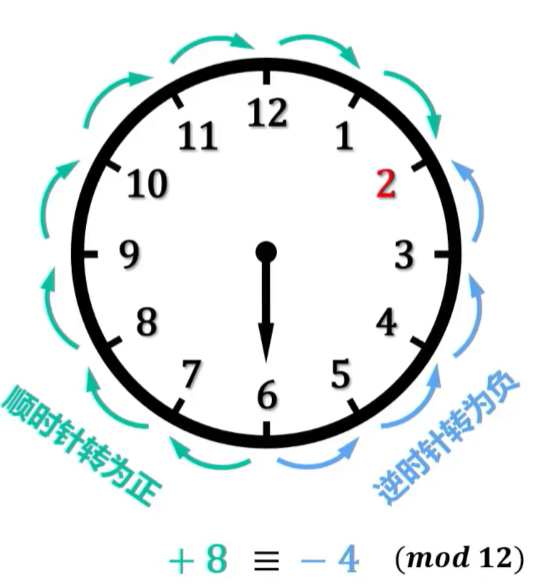
如果讲时钟的指针从6拨到2，可以两种操作方式。
- 逆时针拨动4下
- 顺时针拨动8下
这两种方式是等价的，按照逆时针为负顺时针为正的话，在时钟拨动的案例中，+8 是-4以 12 为模的补数。
模的概念：
- 模(或称模数)是一个数值计量系统的计量范围，记作mod或M。
- 只要确定了“模”，就可找到一个与负数等价的正数来代替此负数，该正数就是负数的补数。
- 超出计量范围的数都应该自动舍去模数
【举例】
6+13=19三7(mod 12)
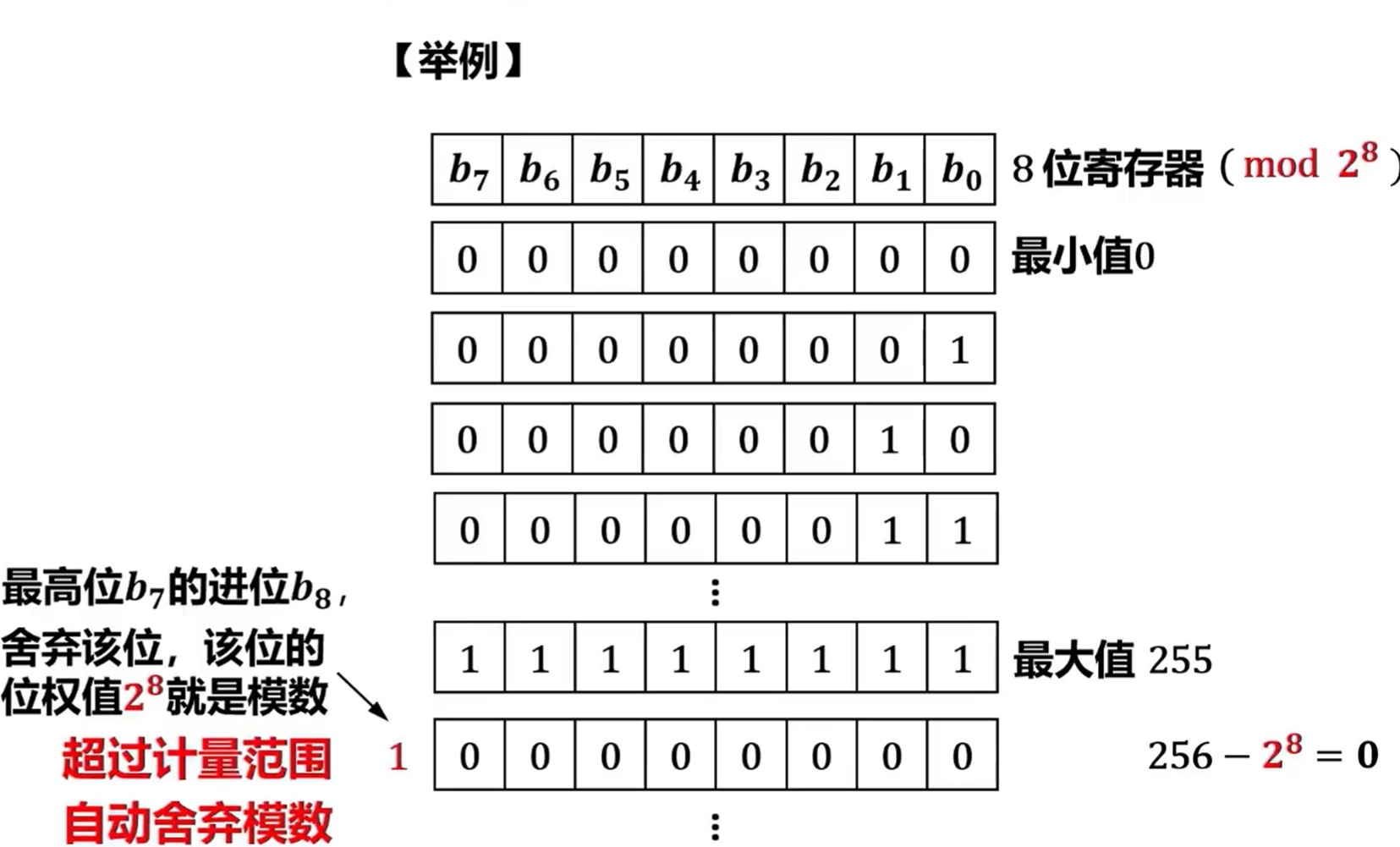
在该8位寄存器中，能表示的无符号定点数最大数值为\(2^{8}\),最小值为0。当超过最大值的时候就会舍弃模数（向前再进一位），而后这8位都从0开始。
补数的特点：
- 一个负数可用它的正补数来替代，而这个正补数可以用模数加上负数本身求得。
- 一个正数和一个负数互为补数时，它们绝对值之和即为模数
- 正数的补数即该正数本身（这个不用深究，记住就行）
对特点1来说，前面时钟的案例中[-4]的补数=12+(-4)=+8,同样的[-9]的补数为12+[-9]=+3
对特点2来说，|+8|+|-4|=12，|-9|+|3|=12
寻找一个负数的整补数的意义何在呢？
- 把减法运用加法实现
- 符号位也可以直接参与运算
这样在计算机内部就可以使用加法器来实现减法运算，而不必专门设置减法器，因而降低了硬件的复杂度和成本。
最后因为16超过模数范围自动舍弃模数即16-12得到最终结果4。
补码
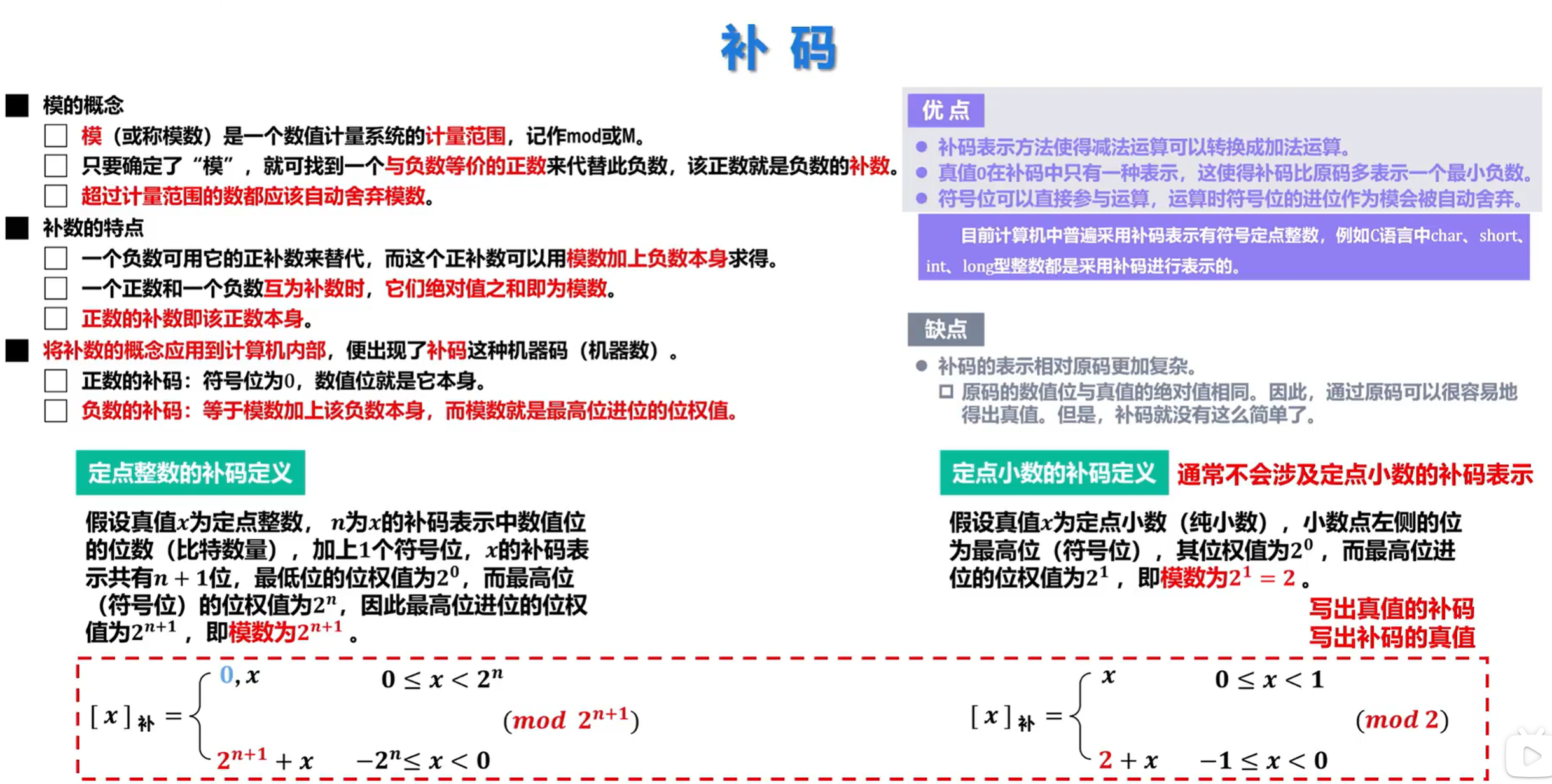
将补数的概念应用到计算机内部，便出现了补码这种机器码（机器数）。
-
正数的补码：符号位为0，数值位就是它本身。
-
负数的补码：等于模数加上该负数本身，而模数就是最高位进位的位权值。
定点整数的补码定义：
假设真值x为定点整数，n为x的补码表示中数值位的位数（比特数量），加上1个符号位，x的补码表示共有n+1位，最低位的位权值为\(2^{0}\)，而最高位（符号位）的位权值为\(2^{n}\)，因此最高位进位的位权值为\(2^{(n+1)}\)，即模数为\(2^{(n+1)}\)。
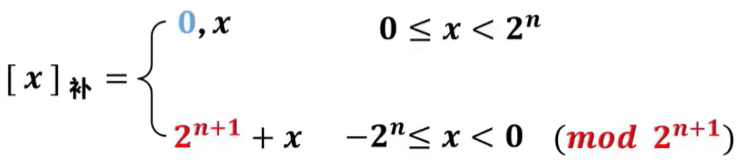
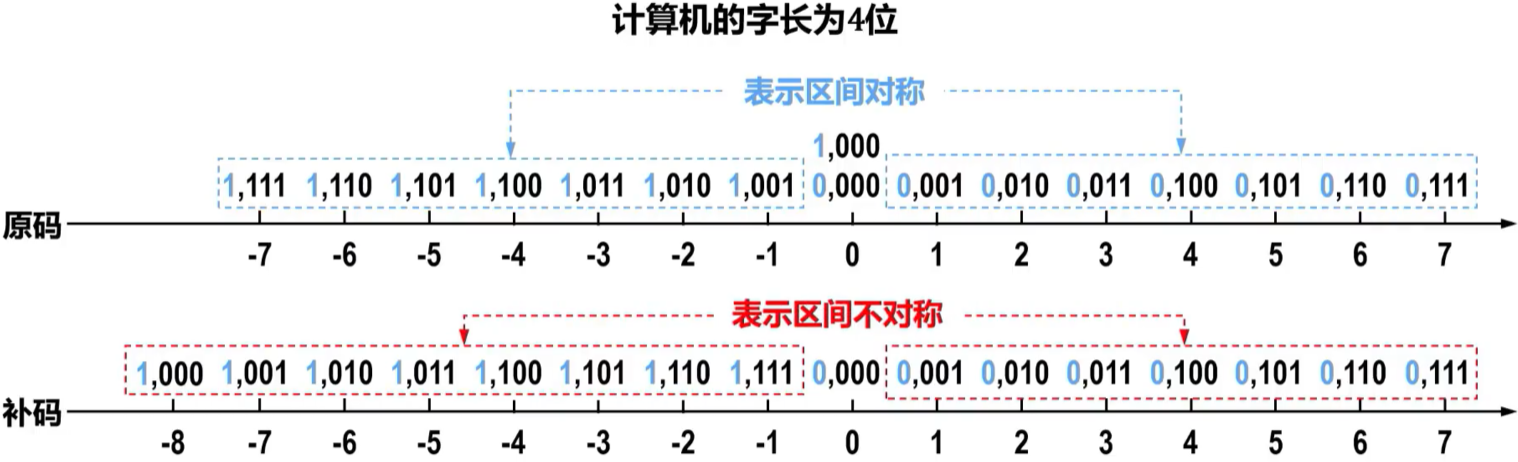
0在补码和原码表示时候的区别：
可以看出正数的原码与补码相同，而负数的原码和补码是不同的。
0在原码中有两种表示形式，但是在补码中只有一种表示形式，因此补码可以比原码多表示一个数。
定点小数的补码定义:
假设真值x为定点小数（纯小数），小数点左侧的位为最高位（符号位），其位权值为\(2^{0}\)，而最高位进位的位权值为\(2^{1}\)，即模数为\(2^{1}\)=2。
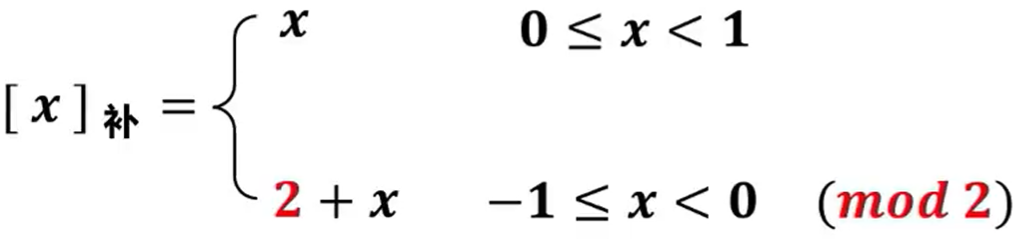
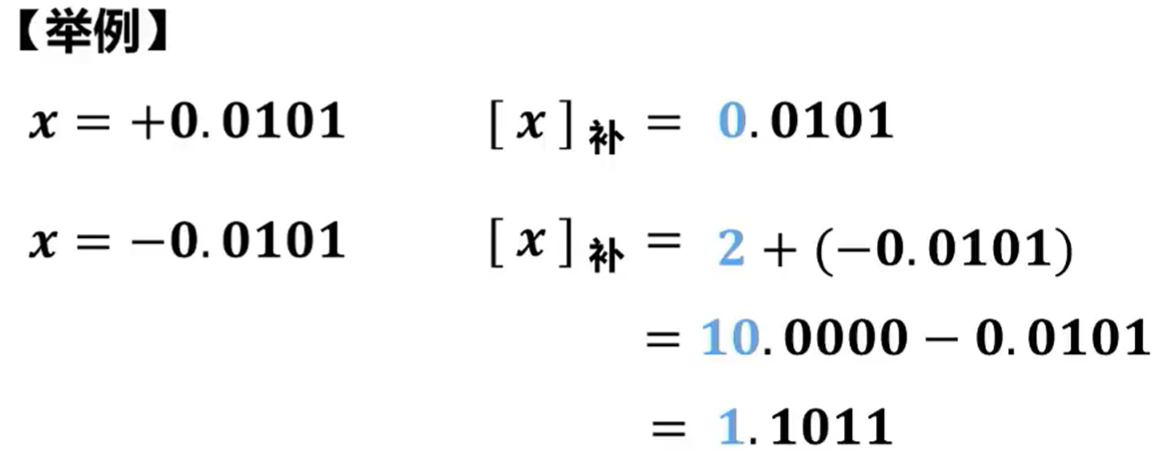
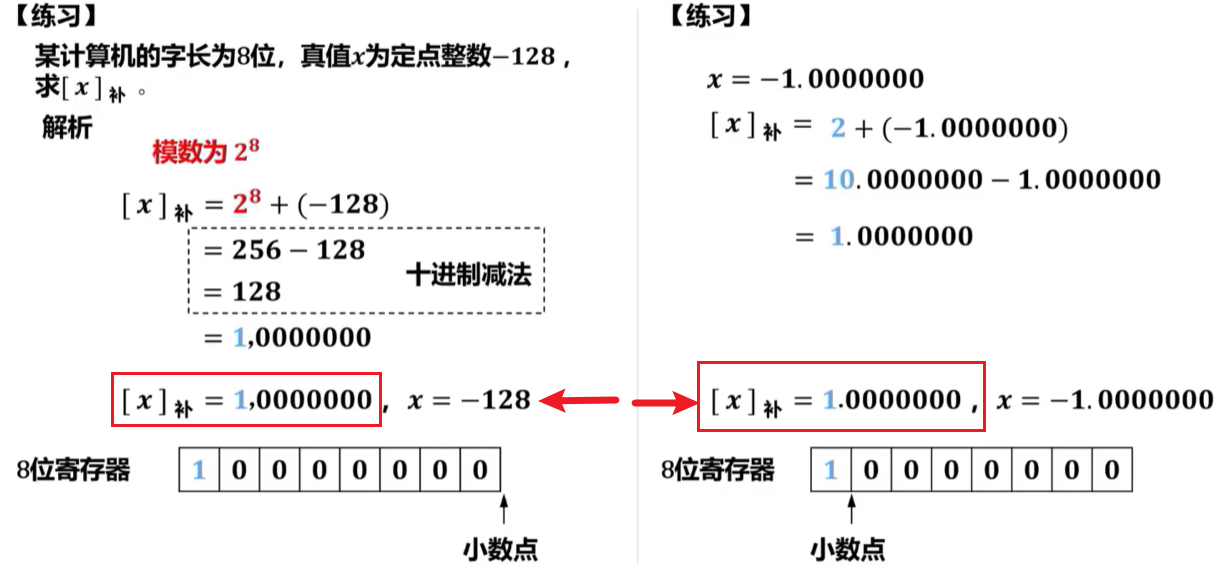
现代计算机中多采用IEEE754标准表示浮点数，而其中的定点小数采用原码表示，因此通常不会涉及定点小数的补码表示。
相关参考：https://www.cnblogs.com/kevinq/p/4480563.html
补码优缺点：
优点：
-
表示方法使得减法运算可以转换成加法运算。
-
真值0在补码中只有一种表示，这使得补码比原码多表示一个最小负数。
-
符号位可以直接参与运算，运算时符号位的进位作为模会被自动舍弃。
目前计算机中普遍采用补码表示有符号定点整数，例如C语言中char、short、int、long型整数 都是采用补码进行表示的。
缺点：
- 补码的表示相对原码更加复杂。
□原码的数值位与真值的绝对值相同。因此，通过原码可以很容易地得出真值。但是，补码就没有这么简单了。
总结：
反码
怎么从原码快速得到补码呢？
在转换原码到补码时候，原码的符号位保持不变，将原码的数值为皆按位取反，之后再在末位+1，即刻得到补码。
而中间的这个末位+1前的就是反码(即原码符号位不变，数值位按位取反得到反码)。
反码通常用来作为由原码求补码或者由补码求原码的中间过渡。
-
正数的反码：符号位为0，数值位就是它本身。
-
负数的反码：符号位为1，数值位就是真值数值位取反。
定点整数的反码定义：
假设真值x为定点整数，n为x的反码表示中数值位的位数（比特数量）。
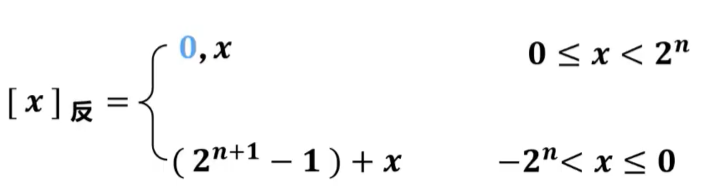
第二个的推导过程：
根据本节的第一张从原码到补码的转换可以得出，原码的反码=该原码的补码-1，在补码的章节中我们知道当-\(2^{n}\) < x ≤0时，该定点整数的补码为\(2^{n+1}\)+x。故进而可以得出此时的定点整数的反码表示为(\(2^{n+1}\)-1)+x。
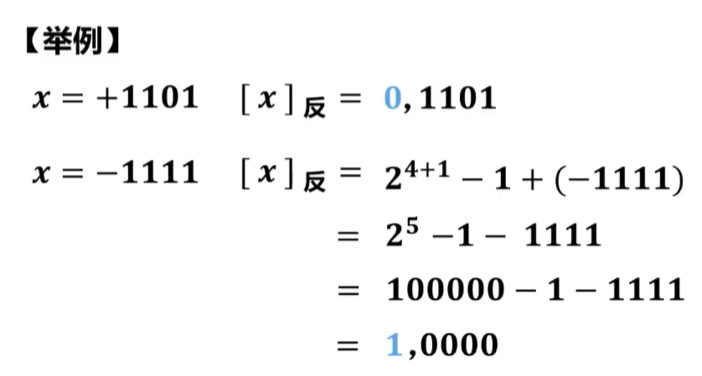
定点小数的反码定义
假设真值x为定点小数， n为x的反码表示中数值位的位数（比特数量）。
当0≤x<1时，其反码为其本身，当-1≤x<0时，根据原码转换补码可知，反码=补码-1,此时的位权值为0，减去的为\(2^{0}\)，推广到小数所应减去的是负的纯小数最低位的位权值为\(2^{-n}\)。又由补码这一章节得知当-1≤x<0时的定点小数的补码为2+x，故得出定点小数的反码定义如下：
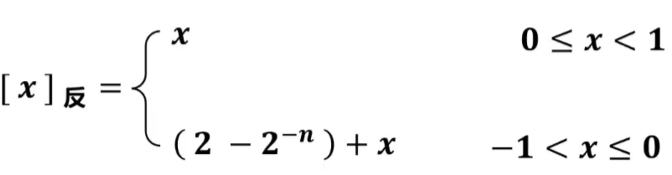
注意：真值0在反码中有两种不同的表示。
原码、反码和补码对比：
真值加法与反码加法对比：
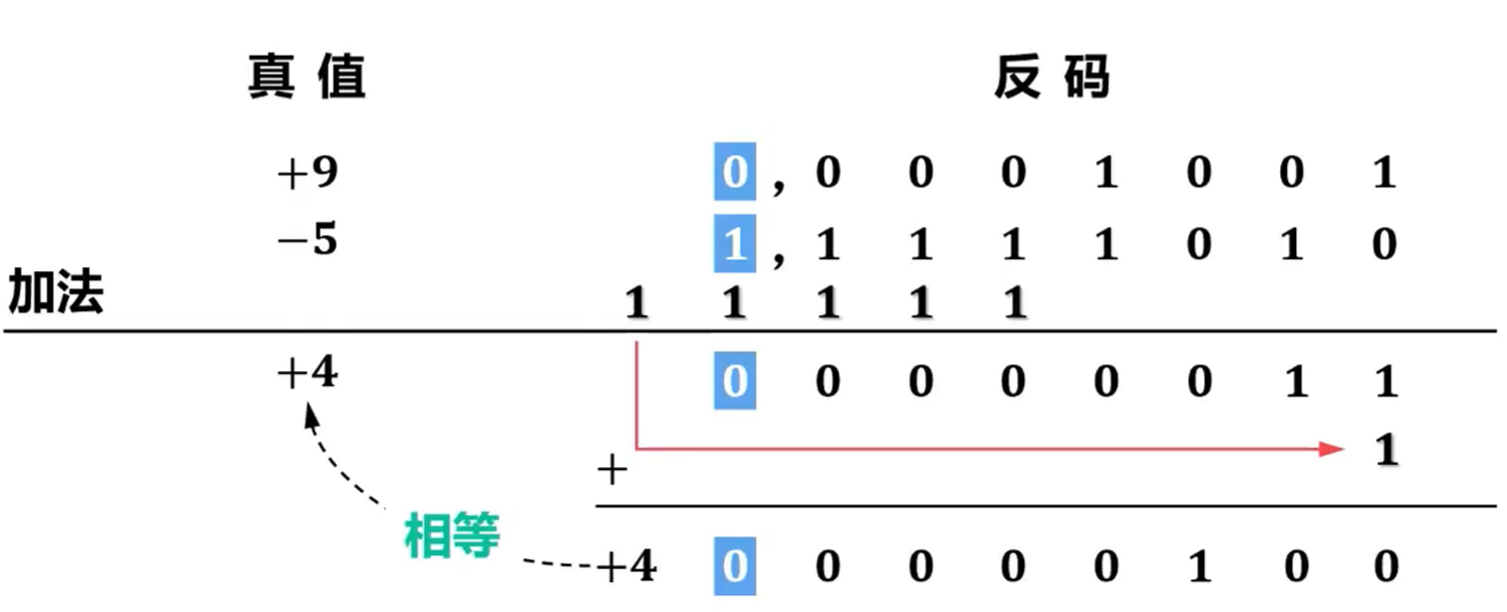
可以看出，如果符号位的进位知识简单地向前进位则与真值的加法结果不同，但是将符号位的进位再加到末位进行计算的得到结果和真值加法计算的结果是一样的。
进而我们可以得到反码的优缺点如下：
| 优点 | 缺点 |
|---|---|
| 符号位可以参与运算 | 1、最高位（符号位）产生的进位要加到运算结果的低位（循环进位） 2、真值0在反码中有两种不同的表示 |
反码在计算机中很少使用，一般是作为原码转补码或补码转原码的中间值。
原码、反码和补码优缺点对比：
| 原码 | 补码 | 反码 |
|---|---|---|
| 优点： 表示方法简单直观 缺点： 1、符号位不能直接参与运算 2、真值0在原码中有两种不同的表示 原码在计算机中目前仅仅用于表示浮点数的尾码。 |
优点： 1、补码表示方法使得减法运算可以转换成加法运算。 2、真值0在补码中只有一种表示，这使得补码比原码和反码多表示一个最小负数。 3、符号位可以直接参与运算，运算时符号位的进位作为模会被自动舍弃。 缺点： 补码的表示比原码复杂。 原码的数值位与真值的绝对值相同。通过原码可以很容易地得出真值。但是，补码就没有这么简单了。 通常不会涉及定点小数的补码表示。 |
优点： 符号位可以参与运算。 缺点： 1、最高位(符号位)产生的进位要加到运算结果的低位(循环进位) 2、真值0在反码中有两种不同的表示 反码在计算机中目前很少被使用。通常用来作为由原码求补码或者由补码求原码的中间过渡。 |
移码
移码就是在真值上加一个常数\(2^{n}\)。移码只用于定点整数的表示。
在数轴上，移码所表示的范围对应于真值在数轴上的范围向轴的正方向移动\(2^{n}\)个单元，如图所示。
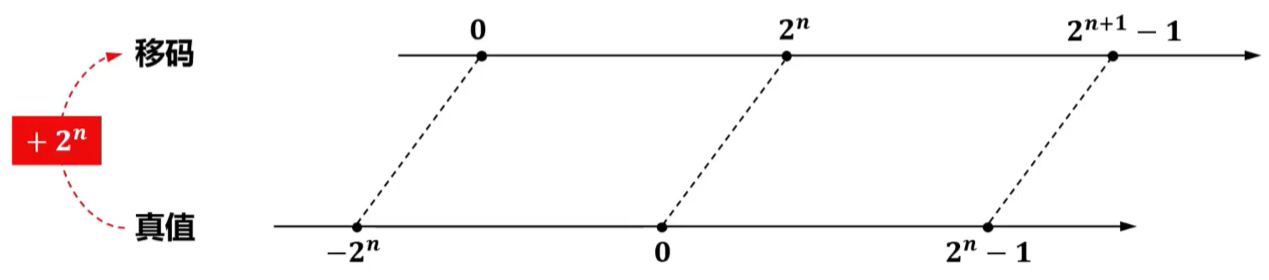
移码定义：
假设真值x为定点整数，n为x的移码表示中数值位的位数（比特数量）。
\([x]_{移}\)=x+\(2^{n}\),-\(2^{n}\)≤x<\(2^{n}\)
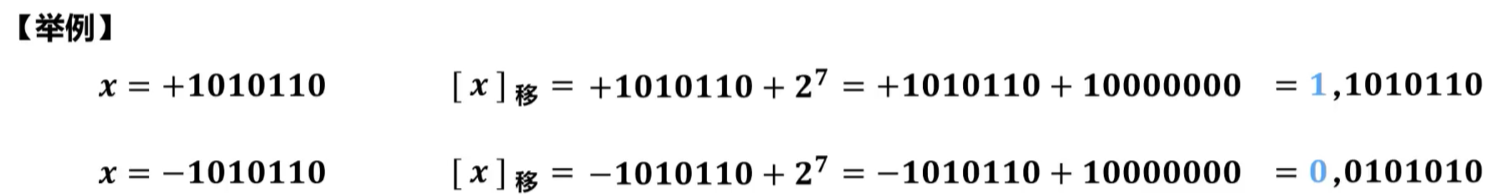
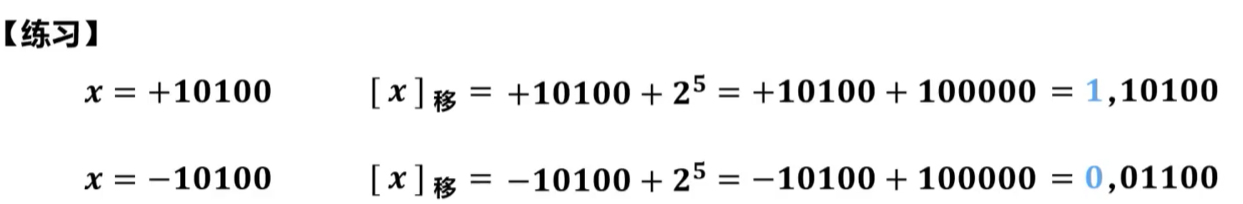
对于0来说，真值0在移码中只有一种表示形式。
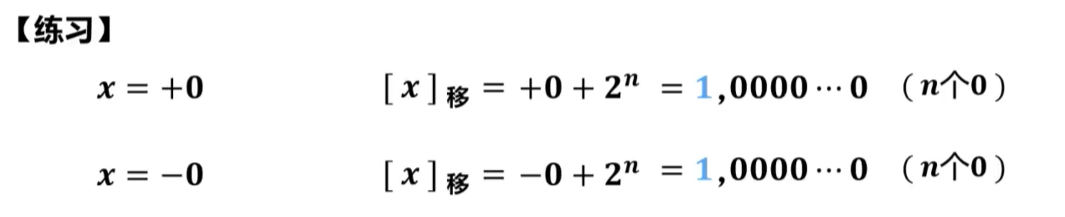
原码、补码、反码和移码对比：
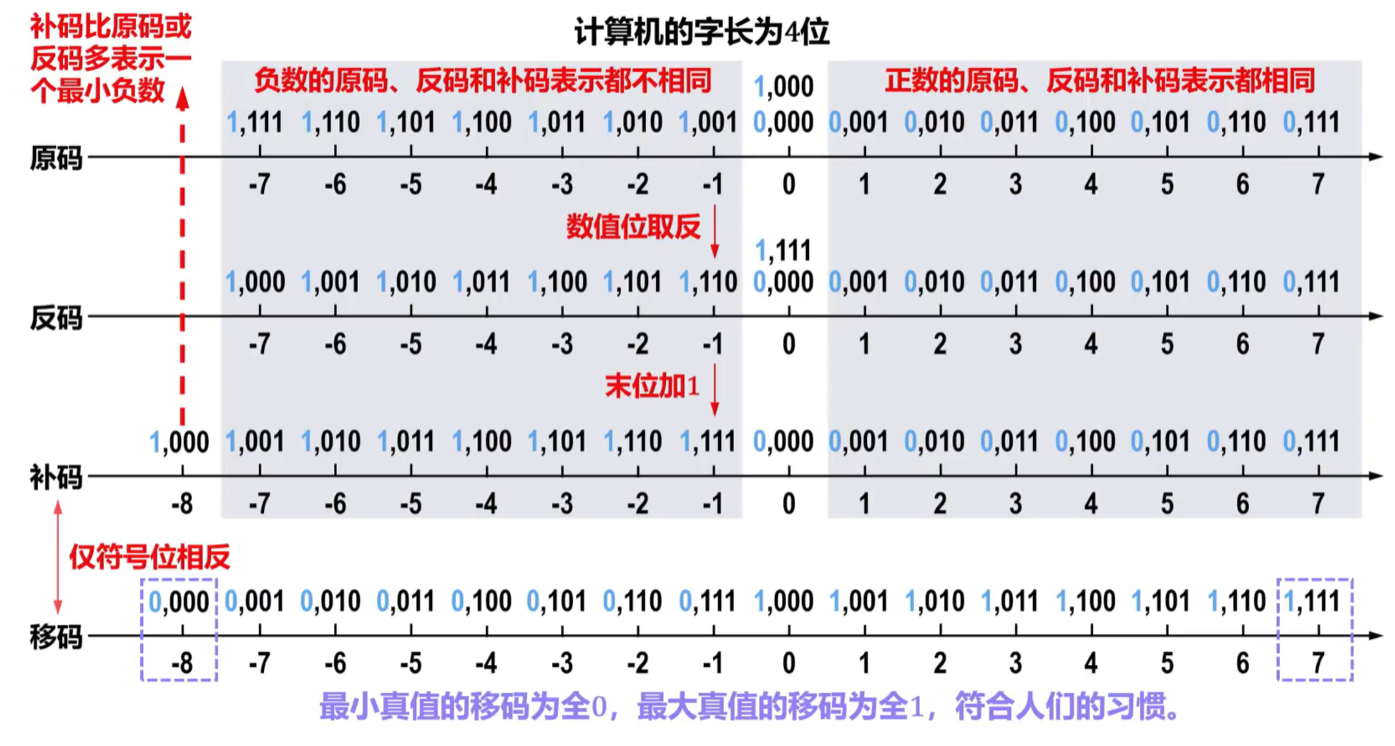
移码优点：
- 真值0在移码中只有一种表示。
- 移码保持了真值原有的大小顺序，可以直接比较大小。
- 最小真值的移码为全0，最大真值的移码为全1，符合人们的习惯。
- 当浮点数的阶码用移码来表示时，就能很方便地比较阶码的大小。
原码、补码、反码和移码的转换
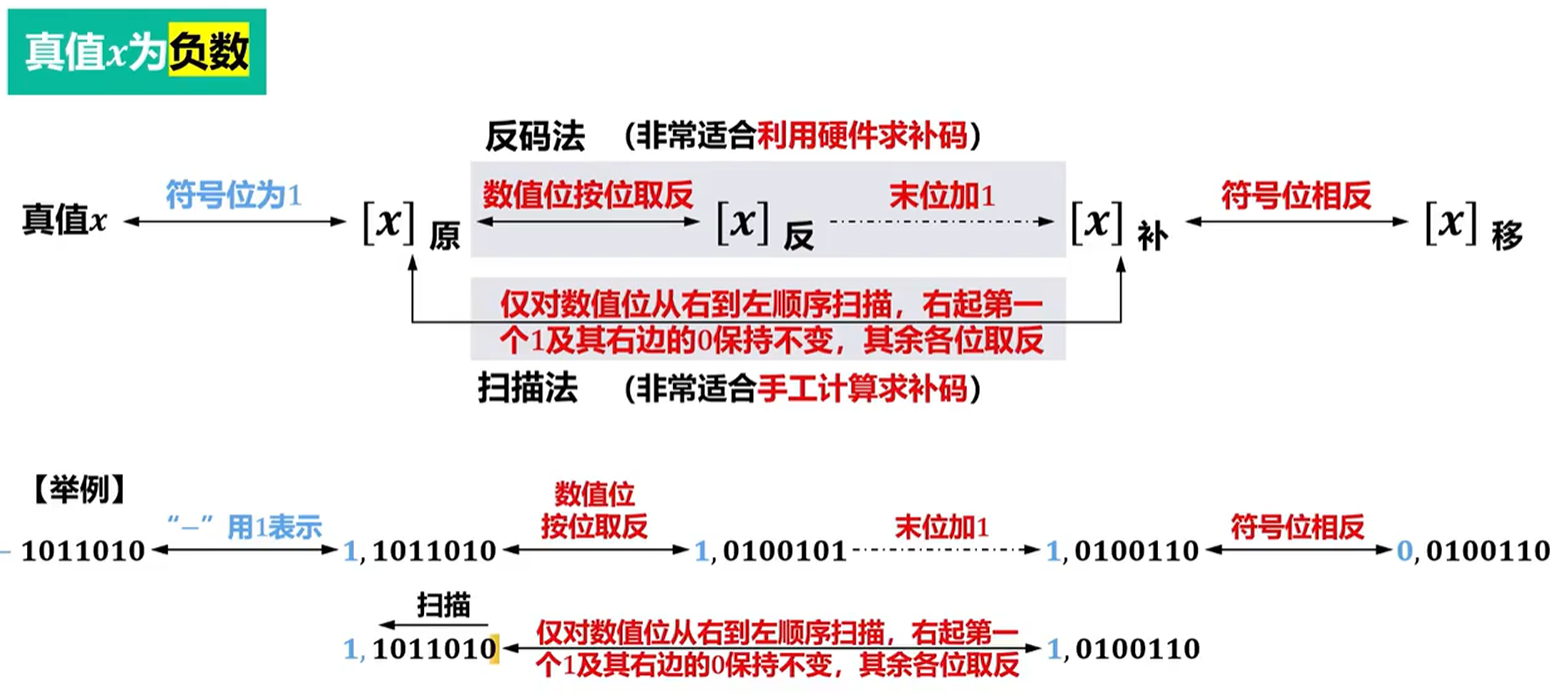
由图可以得出：补码的补码是原码（原码与补码互为补码）。
✏️将一个真值的补码全部位按位取反并末位加1即刻得到该真值的负数的补码。
习题
【习题1】对真值0具有唯一表示形式的机器数（机器码）是（C）。
A.原码
B.补码和反码
C.移码和补码
D.以上都不对
解析：
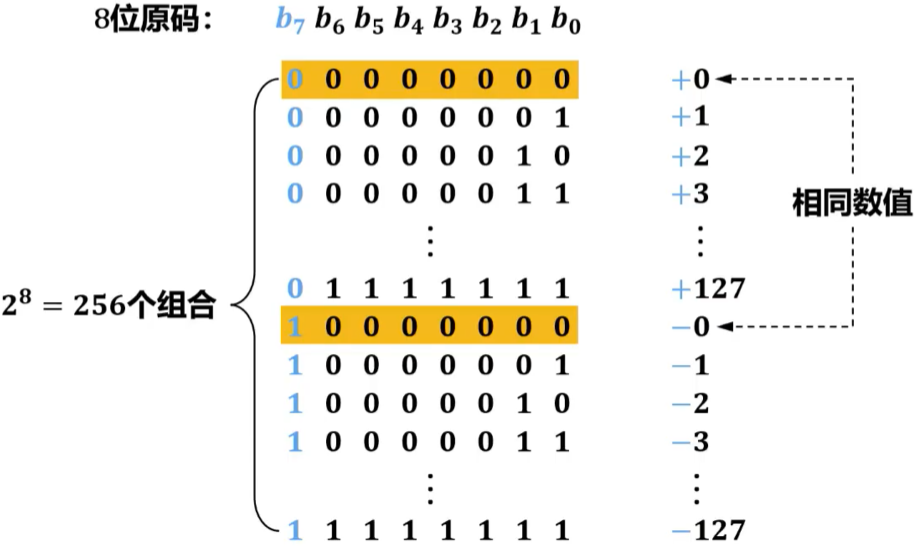
【习题2】8位原码能表示的不同数据的数量是（C）。
A. 127
B. 128
C. 255
D. 256
解析：
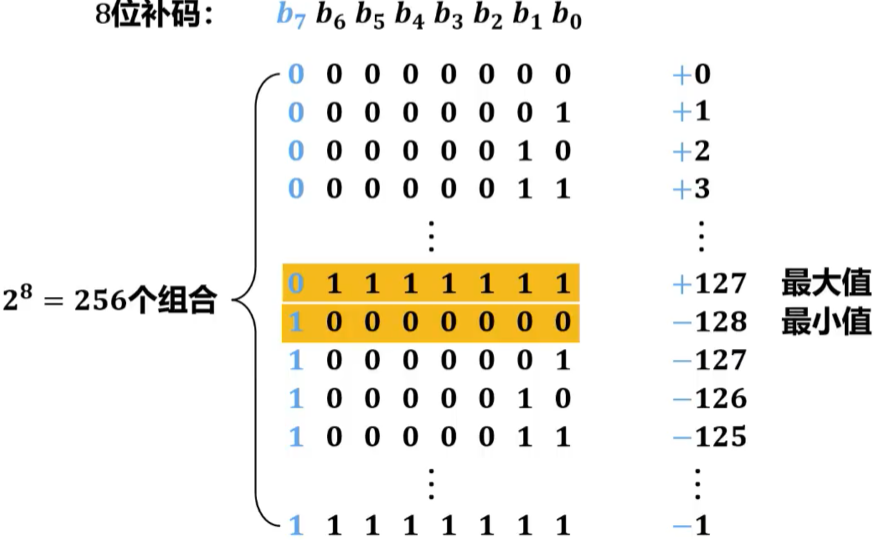
【习题3】某机器字长为8位，机器码采用补码，则机器码所能表示的范围是（B）。
A.-127~+127
B.-128~+127
C.-128~+128
D.以上都不对
解析：
【习题4】若\([x]_{补}\)=1，0110100，则\([x]_{原}\)是（D）。（D）。
A.0,1001011
B.0,1001100
C.1,1001011
D.1,1001100
解析：
【习题5】若[x]补=1，0110100，则x是（D）。
A. +75
B.+76
C.-75
D.-76
解析同上。
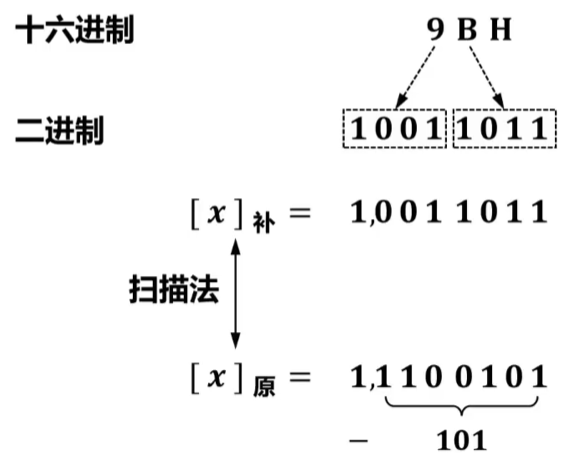
【习题6】设机器数采用补码形式，若寄存器内容为9BH，则对应的十进制数是（C）。
A. -27
B.-97
C. -101
D. 155
解析：
【习题7】假定十进制数为-66，按补码形式存放在一个8位寄存器中，该寄存器的内容用十六进制表示为（）。
A. C2H
В. ВЕН
C. BDH
D. 42H
【习题8】已知\([x]_{补}\)补=1，0110100，则\([-x]_{补}\)是（）。
A.0,1001011
B.0,1001100
C. 1, 1001011
D.1,1001100
【习题9】已知[x]补=1，0000000，则[—x]补是（D）。
A. 0, 1111111
B.0,0000001
C.1,0000000
D.无法表示
【习题10】设x为真值，\(x^{*}\)为其绝对值，满足\([\)-x*\(]_{补}\)=\([-x]_{补}\)的条件是（B）。
A.x任意
B.x为正数
C.x为负数
D.以上都不对
补码的表示是唯一的。
【2015年题13】由3个“1”和5个“0”组成的8位二进制补码，能表示的最小整数是（B）。
A. -126
B. -125
C.-32
D. -3
【2021年题13】已知带符号整数用补码表示，变量x，y，z的机器数分别为FFFDH，FFDFH，7FFCH，下列结论中，正确的是(D)。
A.若x，y和z为无符号整数，则z<x<y
B.若x，y和z为无符号整数，则x<y<z
C.若x，y和z为带符号整数，则x<y<z
D.若x，y和z为带符号整数，则y<x<z
欢迎关注公众号：愚生浅末。
