数据结构代码题-栈、队列
栈、队列
栈
栈的定义
#define MaxSize 100 //储存空间的初始分配量
typedef int ElemType;
typedef struct{
int top; //栈顶指针
ElemType data[MaxSize]; //存放元素的动态数组空间
}sqstack;
链栈的数据结构描述
typedef struct Linknode{
ElemType data; //数据域
struct Linknode *next; //指针域
} *LiStack; //栈类型定义
栈的基本运算:
sqstack *init()//初始化栈s
{
sqstack *s=(sqstack *)malloc(sizeof(sqstack));
s->top=-1;//栈顶指针最初为-1
return s;
}
void destroy(sqstack *s)//销毁栈
{
free(s);
}
bool stackempty(sqstack *s)//判断栈是否为空
{
return (s->top==-1);//为空,返回1
}
int push(sqstack *s,int e)//入栈操作
{
if(s->top==MaxSize-1)//判断栈是否溢出
return 0;//溢出,报错
s->top++;//没溢出,栈顶指针指向上一个
s->data[s->top]=e;//将元素入栈至栈顶位置
return 1;
}
int pop(sqstack *s)//出栈操作
{
int e = 0;
if(s->top==-1)//判断栈是否为空0
return 0;//为空,报错
e=s->data[s->top];//元素e存储栈顶位置元素
s->top--;//栈顶指向下一个
return e;
}
bool gettop(sqstack *s,char e)//取向栈顶元素
{
if(s->top==-1)//判断栈是否为空0
return false;//为空,报错
else e=s->data[s->top];//将元素e存储栈顶元素
return true;
}
04.设单链表的表头指针为L,结点结构由data和next两个域构成,其中data域为字符型。试设计算法判断该链表的全部n个字符是否中心对称。例如xyx、xyyx都是中心对称。
算法思想:
使用栈来判断链表中的数据是否中心对称。 让链表前一半元素依次进栈。 在处理链表的后一半元素时,当访问到链表的一个元素后,就从栈中弹出一个元素,两个元素比较,若相等,则将链表中的下一个元素与栈中再弹出的元素比较,直至链表到尾。这时若栈是空栈,则得出链表中心对称的结构;否则,当链表中的一个元素与栈中弹出的元素不等时,结论为链表非中心对称,结束算法执行。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define MAN_ERR 0
#define MAN_OK 1
struct node
{
char data;
struct node * next;
};
typedef struct node Node;
typedef struct node * link;
void create_link(link *head)
{
*head = (link)malloc(sizeof(Node));
(*head)->next = NULL;
}
int is_malloc_ok(link new_node)
{
if(new_node == NULL)
{
printf("malloc error!\n");
return MAN_ERR;
}
return MAN_OK;
}
void create_node(link head,link *new_node,int n)
{
int i;
char a;
link p;
p = head;
for(i=1;i<=n;i++)
{
scanf("%c",&a);
*new_node =(link)malloc(sizeof(Node));
while(is_malloc_ok(*new_node)==0)
{
*new_node =(link)malloc(sizeof(Node));
}
(*new_node)->data = a;
while(p->next != NULL)
{
p = p->next;
}
p->next = *new_node;
(*new_node)->next = NULL;
}
}
int judge_link(link head, int n)
{
link p;
p = head->next;
char s[10];
int i, j;
for(i=1;i<=n/2;i++){
s[i]=p->data;
p = p->next;
}
if(n%2==1){
p = p->next;
}
j = i-1;
for(i=j;i>=1;i--)
{
if(p->data == s[i])
{
p = p->next;
}
else
{
break;
}
}
if( i!=0)
{
return 0;
}
else
{
return 1;
}
}
void display_link(link head)
{
link p = NULL;
if(head == NULL)
{
printf("link is empty!\n");
return;
}
if(head->next == NULL)
{
return;
}
else
{
p = head->next;
while(p != NULL)
{
printf("data = %c\n",p->data);
p = p->next;
}
}
}
void release_link(link * head)
{
link p;
p = *head;
if(p == NULL)
{
printf("link is empty!\n");
return;
}
else
{
p = (*head)->next;
while(p != NULL)
{
(*head)->next = p->next;
free(p);
p = p->next;
}
free(*head);
*head = NULL;
}
}
int main()
{
link head = NULL;
link new_node = NULL;
int n, a;
printf("要输入几位数据:\n");
scanf("%d",&n);
getchar();
create_link(&head);
create_node(head,&new_node,n);
display_link(head);
a=judge_link(head,n);
if(a==0)
{
printf("不是中心对称\n");
}
if(a==1)
{
printf("是中心对称\n");
}
release_link(&head);
display_link(head);
return 0;
}
05.设有两个栈s1、s2都采用顺序栈方式,并共享一个存储区[0,...,maxsize—1],为了尽量利用空间,减少溢出的可能,可采用栈顶相向、迎面增长的存储方式。试设计s1、s2有关入栈和出栈的操作算法。
算法思想:
两个栈共享向量空间,将两个栈的栈底设在向量两端,初始时,s1栈顶指针为-1,s2栈顶指针为maxsize.两个栈顶指针是否相邻时为栈满.两个栈顶相向,迎面增长,栈顶指针指向栈顶元素.
#define maxsize 100 //两个栈共享顺序存储空间所能达到的最多元素数
#define elemtp int //初始化为100
typedef struct
{
elemtp stack[maxsize]; //栈空间
int top[2]; //top为两个栈顶指针
} stk;
stk s; //s是如上定义的结构类型变量,为全局变量
(1)入栈操作
int push(int i, elemtp x){
//入栈成功返回1,否则返回0
if (i < 0 || i > 1){
printf("栈号输入不对\n");
exit(0);
}
if (s.top[1] - s.top[0] == 1){
printf("栈已满\n");
return 0;
}
switch(i){
case 0:s.stack[++s.top[0]] = x;
return 1;
break;
case 1:s.stack[--s.top[1]] = x;
return 1
}
}
(2)退栈操作
elemtp pop(int i){
//i代表栈号,i=0时为s1栈,i=1时为s2栈
//入栈成功返回1,否则返回0
if (i<0||i>1){
printf("栈号输入错误\n");
exit(0);
}
switch ((i))
{
case 0:
if (s.top[0] == -1){
printf("栈空\n");
return -1;
} else {
return s.stack[s.top[0]--]
}
case 1:
if (s.top[1] == maxsize){
printf("栈空\n");
return -1;
} else {
return s.stack[s.top[1]++];
}
}//switch
}
队列
队列的顺序存储类型描述
#define MaxSize 50 //定义队列中元素的最大个数
typedef struct{
ElemType data[MaxSize]//存放队列元素
int front,rear;//队头指针和队尾指针
} SeQueue;
队列的链式存储
typedef struct { //链式队列结点
ElemType data;
struct LinkNode *next;
} LinkNode;
typedef struct{ //链式队列
LinkNode *front, *rear;//队列的队头和队尾指针
} LinkQueue;
链表实现循环队列
#include <stdio.h>
#include <stdlib.h>
typedef int ElemType;
typedef struct LNode {
ElemType data;
struct LNode *next;
} LNode, *LinkList;
void CircleQueue(LinkList front, LinkList rear) {
//进行初始化
front = (LinkList) malloc(sizeof(LNode));
rear = front;
rear->next = front;
//入队两个元素
EnQueue(front,rear,3);
EnQueue(front,rear,4);
//出队
Dequeue(front,rear);
Dequeue(front,rear);
Dequeue(front,rear);
}
int main() {
LinkList front, rear;
CircleQueue(front, rear);
}
入队
void EnQueue(LinkList front, LinkList &rear, ElemType val) {
LinkList pnew;
if (rear->next == front) {
//rear当前是空节点,如果rear->next== front,说明队列满
//申请新节点
pnew = (LinkList) malloc(sizeof(LNode));
//插入的元素放在rear节点中,而不放在新申请的空节点中
rear->data = val;
rear->next = pnew;
pnew->next = front;
rear = pnew;
} else {
//队列不满,直接放值,rear后移一个节点
rear->data = val;
rear = rear->next;
}
}
出队
void Dequeue(LinkList &front,LinkList rear)
{
if (front==rear)
{
printf("empty queue\n");
}else{
printf("Dequeue->%d\n",front->data);
front=front->next;
}
}
- 若希望循环队列中的元素都能得到利用,则需设置一个标志域tag,并以tag的值为0或1来区分队头指针front和队尾指针rear相同时的队列状态是“空”还是“满”。试编写与此结构相应的入队和出队算法。
算法思想:
思路:利用tag来标记队列空或满的条件如下为:
- tag等于0时,并且Q.front==Q.rear ,则为队空;
- tag等于1时,并且Q.front==Q.rear,则为队满。
队列结构:
#define MaxSize 10;
typedef struct Queue{
int tag;
int front, rear;
int data[MaxSize];
}Queue;
初始化队列:
// 初始化队列
void InitQueue(Queue *Q){
Q.tag = 0;
Q.front = Q.rear = 0;
}
队列判空:
// 判空 空的话返回1,非空返回0
int Empty(Queue Q){
if(tag == 0 && Q.front == Q.rear){
return 1;
}
return 0;
}
队列判满:
// 判满 满的话返回1非满返回0
int Full(Queue Q){
if(tag == 1 && Q.front == Q.rear){
return 1;
}
return 0;
}
入队:
// 入队
int EnQueue(Queue *Q, int n){
// 判满
if(Full(Q)){
return 0;
}
Q.data[Q.rear] = n;
Q.rear = (Q.rear+1)%MaxSize;
// 节点入队后,判断指针是否相等,决定空满标志tag的值
if(Q.rear == Q.front){
Q.tag = 1;
}
return 1;
}
出队:
int DeQueue(Queue *Q, int *e){
if(Empty(Q)){
return 0;
}
e = Q.data[Q.front];
Q.front = (Q.front+1)%MaxSize;
if(Q.front == Q.rear){
Q.tag = 0;
}
return 1;
}
- Q 是一个队列,S 是一个空栈,实现将队列中的元素逆置的算法。
void Inverse(Stack S, Queue Q) {
while (!QueueEmpty(Q)) {
x = DeQueue(Q);
Push(S, x);
}
while (!StackEmpty(S)) {
Pop(S, x);
EnQueue(Q, x);
}
}
- 利用两个栈S1和S2来模拟一个队列,已知栈的4个运算定义如下:
Push(S,x);//元素x入栈
pop(S,x);//S出栈并将出栈的值赋值给x
StackEmpty(S);//判断栈是否为空
stackOverflow(S);//判断栈是否满
如何利用栈的运算来实现该队列的3个运算(形参自己设计)?
Enqueue;//将元素x入队
Dequeue;//出队,并将出队元素存储在x中
QueueEmpty;//判断队列是否为空
算法思想:
利用两个栈s1和s2来模拟一个队列,当需要向队列中插入一个元素时用S1来存放已输入的元素,即S1执行入队操作。当需要出队时,则队S2执行。出栈操作,必须先将S1中所有元素出栈并入栈到S2中,再在S2中出栈即可实现出队操作,而在执行此操作之前必须判断S2是否为空,否则导致顺序混乱。当栈S1和S2都为空时队列为空。
即:
①对S2的出栈操作用作出队,若S2为空则先将S1中所有元素送入S2
②对S1的入栈操作用作入队,若S1满,必须先保证S2为空,才能将S1中的元素全部插入S2中
判断队列为空算法:
int QueueEmpty(Stack S1,Stack S2){
if(StackEmpty(S1)&&StackEmpty(S2)){
return 1;
}
else return 0;
}
入队算法:
//入队算法
int EnQ(Stack *S1,Stack *S2,Elemtype e){
if(!StackOverflow(S1)){
Push(S1,e);
return 1;
}
if(StackOverflow(S1) && !StackEmpty(S2)){
printf("队列满");
return 0;
}
if(StackOverflow(S1) && StackEmpty(S2)){
while(!StackEmpty(S1)){
Pop(S1,x);
Push(S2,x);
}
Push(S1,e);
return 1;
}
}
出队算法:
//出队算法
void DeQueue(Stack *S1,Stack *S2,Elemtype *x){
if(!StackEmpty(S2)){
Pop(S2,x);
}
else if(StackEmpty(S1)){
printf("队列为空");
}
else{
while(!StackEmpty(S1)){
Pop(S1,x);
Push(S2,x);
}
Pop(S2,x);
}
- 【2019统考真题】请设计一个队列,要求满足:①初始时队列为空;②入队时,允许增加队列占用空间;③出队后,出队元素所占用的空间可重复使用,即整个队列所占用的空间只增不减;④入队操作和出队操作的时间复杂度始终保持为O(1)。请回答下列问题:
1)该队列是应选择链式存储结构,还是应选择顺序存储结构?
2)画出队列的初始状态,并给出判断队空和队满的条件。
3)画出第一个元素入队后的队列状态。
4)给出入队操作和出队操作的基本过程。
答案:
(1)链式存储
(2) 初始时,创建只有一个空闲节点的链表,rear,front指针都指向第一个空闲的节点

新增一个元素之后:

队空的判定条件:front=rear
队满的判定条件: rear->next == front
(3)

在插入一个元素之后,一定要确保当前节点的next是下一个空节点

(4)入队和出队操作
出队操作:
移除front指针指向的节点存储的元素,并将front指针向前移动front=front->next

入队操作:

将新元素Element放在Element2之后,同时将rear指向之前移除元素的节点
入队操作:
if(rear->next == front) // 队满
{
在rear之后插入一个新节点
Lnode p = (Lnode*)malloc(Lnode);
p->next = rear->next;
rear->next = p;
rear = p;
}
入队元素保存在rear所指向的节点中;
rear=rear->next;
出队操作:
if (front == rear) //队空
{
return 0;
}else{
// 如果对列不为空
Eletype element = front->data;
front = front->next;
return element;
}
栈和队列的应用
01.假设一个算术表达式中包含圆括号、方括号和花括号3种类型的括号,编写一个算法来判别表达式中的括号是否配对,以字符“\0”作为算术表达式的结束符。
算法思想:
- 初始化一个空栈,顺序读入括号
- 若是右括号则与栈顶元素进行匹配(若匹配,则弹出栈顶元素并进行下一元素 若不匹配,则该序列不合法)
- 若是左括号,则压入栈中
- 若全部元素遍历完毕,栈中仍然存在元素,则该序列不合法
#define ElemType char
#define MaxSize 50
#include<stdio.h>
typedef struct
{
ElemType data[MaxSize];
int top;
}SqStack;
int StackEmpty(SqStack S)
{
if (S.top == -1) //栈空
return 1;
else
return 0; //栈不空
}
int Pop(SqStack* S, ElemType* x)
{
if (S->top == -1) //栈空 不能执行出栈操作
return 0;
*x = S->data[S->top]; //先出栈 指针再减1
S->top--;
return 1;
}
int Push(SqStack* S, ElemType x)
{
if (S->top == MaxSize - 1) //栈满 不能执行入栈操作
return 0;
S->top++; //指针先加1,再入栈
S->data[S->top] = x;
return 1;
}
int GetPop(SqStack S, ElemType* x)
{
if (S.top == -1) //栈空报错
return 0;
*x = S.data[S.top]; //用x存储栈顶元素
return 1;
}
void initStack(SqStack* S)
{
S->top = -1; //初始化栈顶指针
}
int main()
{
SqStack S;
initStack(&S);
char sequence[] = { '[','(',')',']','[',']' };
char* p = sequence;
while (*p == '\0')
{
if (*p == '(' || *p=='[' || *p == '{')
{
Push(&S, *p);
p++;
}
else
{
char getpop;
GetPop(S,&getpop);
//判断是否匹配
if ((getpop=='('&&*p==')')||(getpop == '[' && *p == ']') || (getpop == '{' && *p == '}'))
{
char pop;
Pop(&S, &pop);
p++;
}
else
{
printf("该序列不合法!");
return 0;
}
}
}
if (StackEmpty(S)) //判断最后栈是否为空
printf("该序列合法!");
else
printf("该序列不合法!");
return 0;
}
02.按下图所示铁道进行车厢调度(注意,两侧铁道均为单向行驶道,火车调度站有一个用于调度的“栈道”),火车调度站的入口处有n节硬座和软座车厢(分别用H和S表示)等待调度,试编写算法,输出对这n节车厢进行调度的操作(即入栈或出栈操作)序列,以使所有的软座车厢都被调整到硬座车厢之前。

#include<stdio.h>
#include<stdlib.h>
#define maxsize 30
typedef struct {
char data[maxsize];
int top;
}SeqStack; //定义栈
void Initial(SeqStack *S){
S->top = -1;
} //初始化
int IsFull(SeqStack *S){
return S->top==maxsize-1;
}
int IsEmpty(SeqStack *S){
return S->top==-1;
}
int Push(SeqStack *S,char x){
if(IsFull(S))
return 0;
S->data[++S->top]=x;
return 1;
} //入栈
char Pop(SeqStack *S){
char c;
if(IsEmpty (S))
return 0;
c = S->data[S->top];
S->top--;
return c;
} //出栈
void Railway(SeqStack *S){
int i,j=0,n=20;
char train[20] = { 'H','S','S','S','H','S','H','H','S','S','H','S','H','S','H','S','S','H','H','H' }, result[20];
for(i=0;i<n;i++){
if(train[i]=='S')
result[j++]=train[i]; //将软座车厢存放在数组result中
else{
Push(S,train[i]); //将硬座入栈
}
}
while(!IsEmpty(S)){
for(;j<n;j++){
result[j]=Pop(S); //栈中存储的硬座取出并存放在result剩余的空间内
}
}
for(j=0;j<n;j++){
printf("%c",result[j]); //输出result中的数据
}
}
int main(){
SeqStack *S = (SeqStack*)malloc(sizeof(SeqStack)); //给S分配空间
Initial(S);
Railway(S);
return 0;
}
- 利用一个栈实现以下递归函数的非递归计算:
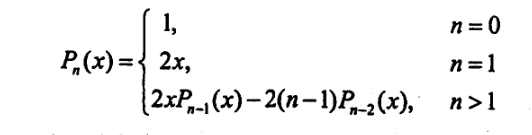
算法思想:
第一步:为递归函数设计一个结构体(Func_val)用于保存函数的n和Pn(x)的值。
第二步:定义一个栈(stack),用于保存递归函数中的n个数据(Func_val类型)。 注:栈stack保存递归函数中从2 到 n的数据
第三步:边出栈边计算Pn(x)的数值(出栈时n从2到n),当栈为空时就计算出了Pn(x)的值。
核心代码:
typedef struct Func_val{
int no;
double val;
}Func_val; // 为递归函数创建数据类型,方便存储
double calculate_val(int n,double x){
Func_val *stack=(Func_val*)malloc(sizeof(Func_val)); //开辟大小为n的栈,栈中存放Func_val数据类型的值
int top = -1; //栈顶指针
double f0, f1; //初始时表示n为0和1时的值
f0 = 1;
f1 = 2 * x;
for (int i = n; i >=2; i--){ //递归函数n个数值依次入栈
top++;
stack[top].no = i;
}
while (top!=-1) //边出栈边计算数值
{
stack[top].val = 2 * x*f1 - 2*(stack[top].no-1) * f0;
f0 = f1; //f0,f1保存本次中n-2和n-1项的值
f1 = stack[top].val;
top--; //出栈
}
if (n == 0){
return f0;
}
else
return f1; //栈空时Pn(x)值计算出来,赋值给f1
}
完整代码:
//递归函数非递归计算
#include<stdio.h>
#include<stdlib.h>
typedef struct Func_val{
int no;
double val;
}Func_val; // 为递归函数创建数据类型,方便存储
double calculate_val(int n,double x){
Func_val *stack=(Func_val*)malloc(sizeof(Func_val)); //开辟大小为n的栈,栈中存放Func_val数据类型的值
int top = -1; //栈顶指针
double f0, f1; //初始时表示n为0和1时的值
f0 = 1;
f1 = 2 * x;
for (int i = n; i >=2; i--){ //递归函数n个数值依次入栈
top++;
stack[top].no = i;
}
while (top!=-1) //边出栈边计算数值
{
stack[top].val = 2 * x*f1 - 2*(stack[top].no-1) * f0;
f0 = f1; //f0,f1保存本次中n-2和n-1项的值
f1 = stack[top].val;
top--; //出栈
}
if (n == 0){
return f0;
}
else
return f1; //栈空时Pn(x)值计算出来,赋值给f1
}
int main(){
int n, x;
double result;
printf("输入非递归函数的n,x:");
scanf("%d %d",&n,&x);
result= calculate_val(n, x);
printf("\n结果为:%f",result);
return 0;
}
- 某汽车轮渡口,过江渡船每次能载10辆车过江。过江车辆分为客车类和货车类,上渡船有如下规定:同类车先到先上船;客车先于货车上船,且每上4辆客车,才允许放上1辆货车;若等待客车不足4辆,则以货车代替;若无货车等待,允许客车都上船。试设计一个算法模拟渡口管理。
算法思想:
此题实际上就是队列的基本操作,唯一的不同就是在入队的时候,对于顺序进行了限制。
- 使用队列Q表示每次载渡的车辆,队列Qp表示客车。Qt表示货车队列;
- 假设Qp中元素足够。则每从队列Qp中出队4个元素。从队列Qt中出队1元素,直到队列Q的长度为10;
- 若队列Qp中元素不充分。则直接使用队列Qt中的元素补齐。
核心代码:
void manager(){
if(IsEmpty(&Qp)!=0&&car<4){
DeQueue(&Qp,&e);
EnQueue(&Q,e);
car++;
count++;
}else if(car==4&&IsEmpty(&Qt)!=0){
DeQueue(&Qt,&e);
EnQueue(&Q,e);
car=0;
count++;
}else{
while(count<=MaxSize&&IsEmpty(&Qt)!=0){
DeQueue(&Qt,&e);
EnQueue(&Q,e);
count++;
}
}
if(IsEmpty(&Qt)==0&&IsEmpty(&Qp)==0){
count=11;
}
}
完整代码:
#include<stdio.h>
#define MaxSize 10
typedef char ElemType;
typedef struct{
ElemType data[MaxSize];
int front, rear;
}SqQueue;
void InitQueue(SqQueue*);
void EnQueue(SqQueue*, ElemType);
void DeQueue(SqQueue*, ElemType*);
int IsEmpty(SqQueue*);
void Mangager(SqQueue*, SqQueue*, SqQueue*);
void PrintQueue(SqQueue);
int main(int argc,char* argv[])
{
SqQueue Q;
SqQueue Qp;//客车
SqQueue Qt;//货车
InitQueue(&Q);
InitQueue(&Qp);
InitQueue(&Qt);
ElemType x='P';
for(int i=0;i<6;i++){
EnQueue(&Qp,x);
}
ElemType y='T';
for(int i=0;i<6;i++){
EnQueue(&Qt,y);
}
int count=0;
int car=0;
ElemType e;
//渡口模拟
while(count<=MaxSize){
if(IsEmpty(&Qp)!=0&&car<4){
DeQueue(&Qp,&e);
EnQueue(&Q,e);
car++;
count++;
}else if(car==4&&IsEmpty(&Qt)!=0){
DeQueue(&Qt,&e);
EnQueue(&Q,e);
car=0;
count++;
}
else{
while(count<=MaxSize&&IsEmpty(&Qt)!=0){
DeQueue(&Qt,&e);
EnQueue(&Q,e);
count++;
}
}
if(IsEmpty(&Qt)==0&&IsEmpty(&Qp)==0)
{
count=11;
}
}
PrintQueue(Q);
return 0;
}
/*---------------------------------------------------------------*/
void InitQueue(SqQueue* Q)
{
Q->front=0;
Q->rear=0;
}
void EnQueue(SqQueue* Q, ElemType x)
{
if(Q->rear==MaxSize-1){
return;
}
Q->data[Q->rear++]=x;
}
void DeQueue(SqQueue* Q, ElemType *x)
{
if(Q->front==Q->rear&&Q->front==0){
return;
}
*x=Q->data[Q->front++];
}
int IsEmpty(SqQueue* Q)
{
if(Q->front==Q->rear){
return 0;
}else{
return -1;
}
}
void PrintQueue(SqQueue Q)
{
while(Q.front!=Q.rear){
printf("%4c",Q.data[Q.front++]);
}
printf("\n");
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号