第三节 单因素方差分析
试验中要考察的指标称为试验指标,影响试验指标的条件称为因素(分类变量),因素所处的状态称为水平,若试验中只有一个因素改变则称为单因素试验,若有两个因素改变则称为双因素试验,若有多个因素改变则称为多因素试验。方差分析就是对试验数据进行分析,检验方差相等的多个正态总体均值是否相等,进而判断各因素对试验指标的影响是否显著,根据影响试验指标条件的个数可以区分为单因素方差分析、双因素方差分析和多因素方差分析。
如果有4组的均数需要比较,如果使用t检验进行两两比较,那需要进行6次。而每次t检验不犯第一类错误的概率为0.95,6次都不犯的概率即是0.95的6次方,所以如果使用t检验进行两两比较,6次t检验 至少有一次犯第一类错误的概率为0.2469,将被放大。如果仍然要使用两两的t检验,就需要控制总的犯第一类错误的概率
各组内部变异(组内变异):反映个体差异(随机变异)的大小
各组均数差异(组间变异):反映了个体差异(随机效用)的影响与可能存在的处理因素的影响之和
总变异=组内变异+组间变异
F检验统计量: F=(SSA/(k-1))/(SSE/(n-k))=MSA/MSE
前提条件:独立性,正态性,方差齐性()
如果得出的结论是多组均数间存在差异,则需要进行事后的两两比较
两两比较中会遇到的一类错误
CER:比较误差,即每做一次比较犯一类错误的概率
EERC:在完全无效假设下的试验误差率,即在H0成立时做完全比较所犯的一类错误的概率,方差分析检验/卡方检验本身控制的就是EERC
MEER:最大试验误差率,即在任何完全或者部分无效假设下,做完全部比较所犯的一类错误的最大概率值,适用范围更广
控制一类错误
直接校正P值:
sidak校正,当无效假设实际成立,即各组均数无差别时,完全两两比较犯第一类错误的概率为1-0.95^(k(k-1)/2),次即EERC,通过控制总的EERC=0.05反向推导没一个检验犯第一类错误的概率,统计软件直接往往将每个检验的屁p值放大(最大放大为1),而固定每个比较的α水准仍为0.05方便阅读
bonferroni校正:大多数实际问题中,都是有些组均数相同,有些不同,因此使用MEER更合适,通过控制CER,使得MEER被控制在所设定的水准内,计算公式为CER=α/c(需要进行比较的次数)
直接校正的缺陷:将两两比较分别进行,不仅使用麻烦,也增加了误差的影响,因为每次两两比较只会用到这一组的数据而利用不到所有的数据,联合检验可解决此类问题,而且对一类错误的控制太严格,结果往往是偏保守的
联合检验:LSD-t检验,LSD最小显著差异,t检验的一个变形,在标准误和自由度的计算上利用了全部样本信息,使得结果更为准确,t检验的标准误和自由度的计算只利用了相应的两组的信息。如果不对检验水准做任何校正,则可以认为LSD是最灵敏,或者最容易得出阳性结论的
常见的联合比较方法:
S-N-K:使用student化的范围分布快速进行检验,将总样本分为多个同质子集,但是组数很多时假阳性较高,一般超过5组就要小心
Tukey:原理类似SNK
Duncan:做了进一步的改进
Scheffe:进行多组的联合检验而不是两两检验,相对比较稳健
Dunnett:需要提供参照组,可进行单侧检验,SCI杂志中经常指定该方法
两两比较方法的选择:
如果两个均数间的比较是独立的,或者虽有多个样本均数,但事先已计划好要做某几对均数的比价,推荐一般t检验
如果存在明确的对照组,要进行的是验证性研究,即计划好的某两个或几个组间(都和对照组)的比价,用LSD发,如果让要要严格的控制,可以先进行bonferroni校正
如果进行的十多个均数间的两两比较(探索研究),此时得到的阳性结论尽可能是真实的,因此要严格控制一类错误
各组人数相等,用Tukey法,该方法此时的检验效能较高
各组人数不相等或者较为复杂时,使用scheffe法更为稳妥,但它相对保守
方差不齐时,最好直接使用非参数检验方法
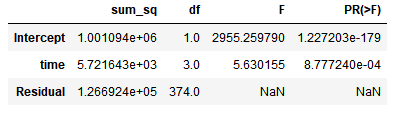
import statsmodels.api as sm # 单因素方差分析的实现 from statsmodels.formula.api import ols ccss.time = ccss.time.astype("str") # 必须将时间从数字调整为category或者str类型 model = ols('index1~time', data=ccss.loc[ccss.s0=='北京',:]).fit() restable = sm.stats.anova_lm(model, typ=3) restable # 多组均数比较,结论拒绝了均值相等的假定,但是没有给出具体的差异信息
1 from statsmodels.sandbox.stats import multicomp as mc # 单因素方差分析事后两两检验的实现 2 res = mc.MultiComparison(ccss.index1, ccss.time).tukeyhsd() # meandiff均值,lower95%置信区间下界,reject是否存在差异 3 res.summary()
| group1 | group2 | meandiff | lower | upper | reject |
|---|---|---|---|---|---|
| 200704 | 200712 | -4.1972 | -8.5083 | 0.1139 | False |
| 200704 | 200812 | -7.897 | -12.2081 | -3.5859 | True |
| 200704 | 200912 | 3.6599 | -0.9332 | 8.253 | False |
| 200712 | 200812 | -3.6998 | -7.9966 | 0.597 | False |
| 200712 | 200912 | 7.8571 | 3.2774 | 12.4368 | True |
| 200812 | 200912 | 11.5569 | 6.9772 | 16.1366 | True |



