SudokuGame 记软工第二次作业

整体概况

1、描述编写整体程序正确过程(含关键代码)
2、整体心路历程及新知分析
3、效能分析、构建之法及整体耗时时间表
4、一些心得体会

GitHub 链接如下:

1、整体开发过程

1> 数独的模型

首先构造出第一行，以此为例构造第一行，第一行可以随机排列，如果不按作业要求的话具有A（9,9）种可能性，也就是说光在第一行随机就可以构造出36万种不同的终盘。
在此我以第一行：1 2 3 4 5 6 7 8 9 为例，介绍一下如何进行变换
以3个为一组，也就是一个宫内为一组，其中组内元素可以调换位置
其中以{1、2、3}、{4、5、6}、{7、8、9}各为一组，向下进行矩阵变换，我先完成的是基本变换也就是不进行组内的全排列变换，可以有两种顺序，我首先按一种顺序进行

第一组第二组第三组 {1、2、3} {4、5、6} {7、8、9}
第二组第三组第二组 {4、5、6} {7、8、9} {1、2、3}
第三组第一组第二组 {7、8、9} {1、2、3}

如此上面三个宫就已经构造完成了。

之后是列变换，以{1、4、7} {2、5、8} {3、6、9}每列为一组，进行类似于以上的列变换，在此不过多赘述了。变换后的结果就如下图所示，其中用红色和蓝色标注的是两个列的变换过程

[9.9] 更新基础作业，模型复杂度增加
根据行之间的关系，由于第一行是通过全排列生成的，因此，第二行上，我通过之前的简单的左右交换，对第一组数据进行全排列的基础上，进行了扩展操作，对第二行的三个三组进行全排列操作，也就是可以生成A（3,3）xA（3,3）xA（3,3）xA（8,8）大概896万种不同的终盘，而随之还可以继续扩展，在此由于题目需求已经满足，没有继续往下写，第二行可以和第三行进行变换，而以4 5 6宫和7 8 9宫为两组的模型，也可以进行交换这样总共理论可以生成A（3,3）xA（3,3）xA（3,3）xA（8,8）x4 大约是3456万种不同的终盘，在此用一张图来表示。

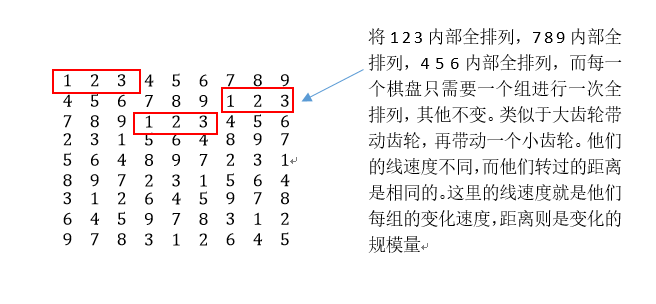
以上就是一个数独终盘的模型构成。我们需要做的就是把它转换成相应代码，以下将详细写一下代码的构造过程

2> 基于基础作业要求的数独C++实现

首先，回答一个问题，大一下的面向对象课上，栋哥讲过这样一个道理，C++面向对象和C的区别在哪里？当时一脸懵逼，之后明白了，C++的类和函数是为了更好的封装。而现在已经深切体会到了这一点，因此现在即使有main函数，也尽量要求自己用函数搞定，因为，好比生产车间，函数就像是人手里的一个工具，而main函数只是一个流水线，流水线是固定的，而工具是任何流水线通用的。
回答完问题，下面就按自己的实现的过程，写一下作业要求.cpp中的函数

1）`void First_Line_Init(int n, struct Sudoku S[])`

此函数为生成第一行函数，其中套用了STL库中的next_permutation（全排列函数），新知识，在以下新知呈现中介绍。我们现在简单的知道，他可以把第一行排列出A（9,9）种不同的组合就可以了。但是由于作业限制第一数位，我最后两位0和6，（0+6）%9 + 1 = 7，因此只有A（8,8）种可能性，同时为了满足10万个数据的要求，我对第一步，也就是我说建模时候的第一次三组数据的第一组数据，也就是作业要求我为{7,x,x}的第一组，进行了全排列，那么也就是A（3,3）*A（8,8），10万个数据量肯定满足了。以下是部分代码
```
        for (int i = 0;i < n;)
        {
            int num[8] = { 1,2,3,4,5,6,8,9 };
            int Times = 0;
             do
    {
	    for (int j = 0;j < 8;j++)
	    {
			    S[i].Finnal_Map[0][j + 1] = num[j];			//下面会写6个原因是A33 = 6所以一个可以出6个不同的矩阵
											//其实感觉，但是如果不是题目的话，最多可以出A33*A33*2个，但是没论证，不确定	
	    }
	    i += 6;
	    Times++;
    } while (next_permutation(num, num + 8) && Times != n/6);
```
}

2）`void Changing(int n, struct Sudoku S[])`

包含void Changing_Row(int i, struct Sudoku S[])（PS：其实开始理解是将行进行变换,改变行，调整到列中，所以起名叫Changing_Row）

此函数进行刚才说的矩阵变换操作，由于列变换相对固定（不必进行列的全排列，如果进行是可以的，但是考虑的问题很多，如果不是要求数据过多，就不尝试了），只单独写了一个列变换函数，而行变换的结果影响列变换的结果，所以直接写在了此函数内。

默认第一组为全排列，因此第二行的前三个数字已经确定，代码与全排列类似，不再贴出，后续的行变换如下：

   for (int i = 0;i < n;i++)
       {
   	    for (int k = 3, l = 0, js = 0;js < 6;l++, k = (k + 1) % 9, js++)
   	    {
   	        	S[i].Finnal_Map[1][l] = S[i].Finnal_Map[0][k];			//剩余第二行
   	    }
   for (int k = 6, l = 0, js = 0;js < 9;l++, k = (k + 1) % 9, js++)
       {
   	    S[i].Finnal_Map[2][l] = S[i].Finnal_Map[0][k];			//第三行
       }
   	    Changing_Row(i, S);		//列变换，构造剩下的6个3x3矩阵
    }

[9.9]更新代码，因为以上代码随模型的复杂而阶梯变化，因此不做移除，相当于是一个进阶版，将第二行的详细构造过程进一步深化，完成与模型同步的代码更新。以下可以认为是本题的核心算法扩容达到216*4万

int num1[3], num2[3], num3[3];
	    for (int i = 0;i < n;)
	    {
		    int Need = i;
		    if (i % 36 == 0)
		    {
			for (int Use = 0; Use < 6; Use++)
			{
				for (int j = 3; j < 6; j++)
				{
					num2[j - 3] = S[Need].Finnal_Map[0][j];
				}
				sort(num2, num2 + 3);
				do
				{
					S[Need].Finnal_Map[1][0] = num2[0];
					S[Need].Finnal_Map[1][1] = num2[1];
					S[Need].Finnal_Map[1][2] = num2[2];
					for (int j = 1; j < 6; j++)
					{
						S[Need + j].Finnal_Map[1][0] = S[Need].Finnal_Map[1][0];
						S[Need + j].Finnal_Map[1][1] = S[Need].Finnal_Map[1][1];
						S[Need + j].Finnal_Map[1][2] = S[Need].Finnal_Map[1][2];
					}
					Need += 6;
				} while (next_permutation(num2, num2 + 3));
			}
			Need = i;
		}
		if (i % 216 == 0)
		{
			for (int j = 0;j < 3;j++)
			{
				num3[j] = S[Need].Finnal_Map[0][j];
			}
			sort(num3, num3 + 3);
			do
		{
			S[Need].Finnal_Map[1][6] = num3[0];
			S[Need].Finnal_Map[1][7] = num3[1];
			S[Need].Finnal_Map[1][8] = num3[2];
			for (int j = 1; j < 36; j++)
			{
				S[Need + j].Finnal_Map[1][6] = S[Need].Finnal_Map[1][6];
				S[Need + j].Finnal_Map[1][7] = S[Need].Finnal_Map[1][7];
				S[Need + j].Finnal_Map[1][8] = S[Need].Finnal_Map[1][8];
			}
			Need += 36;
		} while (next_permutation(num3, num3 + 3));
		Need = i;
	}
	for (int Use = 0; Use < 36; Use++)
	{
		for (int j = 6; j < 9; j++)
		{
			num1[j - 6] = S[i].Finnal_Map[0][j];
		}
		sort(num1, num1 + 3);
		do
		{
			S[i].Finnal_Map[1][3] = num1[0];
			S[i].Finnal_Map[1][4] = num1[1];
			S[i].Finnal_Map[1][5] = num1[2];
			for (int k = 6, l = 0, js = 0; js < 9; l++, k = (k + 1) % 9, js++)
			{
				S[i].Finnal_Map[2][l] = S[i].Finnal_Map[0][k];			
			}
			Changing_Row(i, S);		
			i++;
		} while (next_permutation(num1, num1 + 3));
		
	    }
    }

提交代码中的列变换，其实是为了满足开始随机性的需要，因此进行了随机的两种状况，其实作业基础版本不该写成这样，但是这样做并不会造成重复的发生，我也是在写这份博客的时候刚刚发现的，下面来论证一下，因为左上角的7是固定的，因此以7为第一列往左或者往右换都是一个全新的终盘，而后续的内容，不会影响到该终盘的唯一性，因此即使随机了，但是不会影响最后结果，结果不会重复。同时自己检测过100000份数据的重复率为0，以下贴出代码，由于时间原因，不做修改了。（新版本已经对随机问题进行修正，没有增加这个2倍的量，而100000只是最初设计的程序，只有24万种结果，无法满足题目要求的1000000）
```
 for (int l = 0;l < 3;l++)
   for (int j = l * 3;j < 3 * (l + 1);j++)
   {
       for (int k = 0;k < 3;k++)
       {
   	    if (j == 2 || j == 5 || j == 8)
   		    S[i].Finnal_Map[k + 3][j - 2] = S[i].Finnal_Map[k][j];
   	    else
   		    S[i].Finnal_Map[k + 3][j + 1] = S[i].Finnal_Map[k][j];
       }
   }
   for (int l = 0;l < 3;l++)
   for (int j = l * 3;j < 3 * (l + 1);j++)
   {
       for (int k = 0;k < 3;k++)
       {
   	    if (j == 0 || j == 3 || j == 6)
   		    S[i].Finnal_Map[k + 6][j + 2] = S[i].Finnal_Map[k][j];
   	    else
   		    S[i].Finnal_Map[k + 6][j - 1] = S[i].Finnal_Map[k][j];
       }
   }
```

3）`void Print(int n, struct Sudoku S[])`

提供输出文本功能，核心的话感觉只有一行+一个储存在流中整体输出的思想。
同样在面向对象计算器忘了是第几次作业时候，西瓜学长给我提出了一个计算器批处理改进建议，让我尝试学一下，将内容统一储存在流中，然后整体输出的思想，我之后明白了这个道理，并已经在之前有所应用，而ios::out这个是与之前ios::app不同的。
该函数的核心代码 fstream Out_Put(out, ios::out);
[9.16]更新输出函数
- 其实开始的时候并没有注意到学长的时间要求，以为自己机器测试通过即可，没想到进行了分层，而且测试结果和自己的机子测试结果有所差异。因此我注意并研究了一下自己的输出函数，首先讲一下，fstream的输出问题，就和cin与scanf，cout与printf一样，对于C++的输入输出，和文本的输入输出同样适用，而自己的流文件传输同样存在这个问题，那就是自己的输出慢如狗……前两天在想下一次的结对作业，和组队作业，但是今天就是有一股不服输的劲儿，总觉得对这个项目没有完整通过测评，强迫症驱使下，我开始研究这方面问题。

1】改进第一步 -----从超时10分钟以上，到37秒的救赎

首先自己更改了自己的输出

     f = fopen("sudoku.txt", "w");
     for (int i = 0;i < n;i++)
     {
 	    for (int j = 0;j < 9;j++)
 	    {
 			    fprintf(f, "%d %d %d %d %d %d %d %d %d\n",S[i].Finnal_Map[j][0], S[i].Finnal_Map[j][1], S[i].Finnal_Map[j][2], S[i].Finnal_Map[j][3], S[i].Finnal_Map[j][4], S[i].Finnal_Map[j][5], S[i].Finnal_Map[j][6], S[i].Finnal_Map[j][7], S[i].Finnal_Map[j][8]);
 	    }
 	    fprintf(f, "\n");
     }
     fclose(f);

使用c语言的输出真的可以提升到37秒，这时我只能感受到C++的无限恶意，<<还是没有%d给力啊！

2】进阶版改进，与ACM大佬的对话

其实自己总是好奇为什么自己的改到最后也只有37秒呢？我很不服，觉得既没有递归，也没有冗余的循环，为什么100万要用那么多，于是下午的Linux实践课上，找到了ACM大佬开了小灶。hhhhhhh
下面讲一下方法，就是freopen （补充一下，其实当时可能把freopen和puts等的关系混为一体了。实际加快速速度的是puts的功劳）当然现在VS2017已经要求使用freopen_s了，在网上调查了一下，在预编译设置里加了_CRT_SECURE_NO_WARNINGS,于是美滋滋的编译了一下，自测，3秒解决问题。其实自己在性能分析里看到了99.8%用在了最初版本的out<<S[i].Finnal_Maps[j][k]但是当时并不明白为什么，于是现在明白了，自己的瓶颈完完全全地在自己的输出环节，本次作业收获最大的可能也就在这里吧。感谢K班桔神的教导！代码如下：
```
      int len = 0;
  freopen("sudoku.txt", "w", stdout);
  for (int i = 0; i < n; i++)
  {
      for (int j = 0; j < 9; j++)
      {
  	    for (int k = 0; k < 9; k++)
  	    {
  		    Maps[len++] = S[i].Finnal_Map[j][k] + 48;
  		    Maps[len++] = ' ';
  	    }
  	    Maps[len++] = '\n';
      }
      puts(Maps);
      len = 0;
  }
  fclose(stdout);
```

4）`bool CMD_Check(int argc, string Chk_CMD, string Chk_Num)`

兼容CMD，在之前的测试都完成只有，开始CMD调试，因为CMD适配之后无法在VS2017中调试，所以这步放在最后做
argc -> 参数数量
argv[] -> 参数内容数组
知道这两个，判断是否可以合法，我觉得就已经完成了这个函数了。代码不再罗列出来了。

3>基于选做题的SudokuGame的游戏实现

其实一开始做了大概四个版本的基础作业版本，后面会细讲。而对于游戏而言，需要有乐趣，不能像作业一样1 2 3 4 5 6 7 8 9这样一个个生成，其实在基础作业最开始尝试的时候，写的是随机版本，也因为这个给了我后续的灵感。对于这个新版本的所谓随机，其实就是改变第一行生成函数void First_Line_Init(int n, struct Sudoku S[])，由rand()以及种子srand((unsigned)time(NULL)); “真”随机生成，保证每一盘的随机性。这是第一重要的。
需要一个挖空函数，而挖空函数中，需要一个判别是否唯一解的函数，这两个其实都需要深搜，但是迫于时间，只写了判别唯一解函数，另一个只是随机空，如果无法进行了，就停止，保证30个以上的空是没问题的。以后优化可以在写一个挖空的搜索，这样可以满足不同分级，可以手动控制生成挖空的数目范围。
我在这里提供一张自己制作的各个类之间调用的图，来指明每一个函数的操作。后期，我会把一些类自己的支持函数修改为private，在自己的源码里还没有来的及修改。

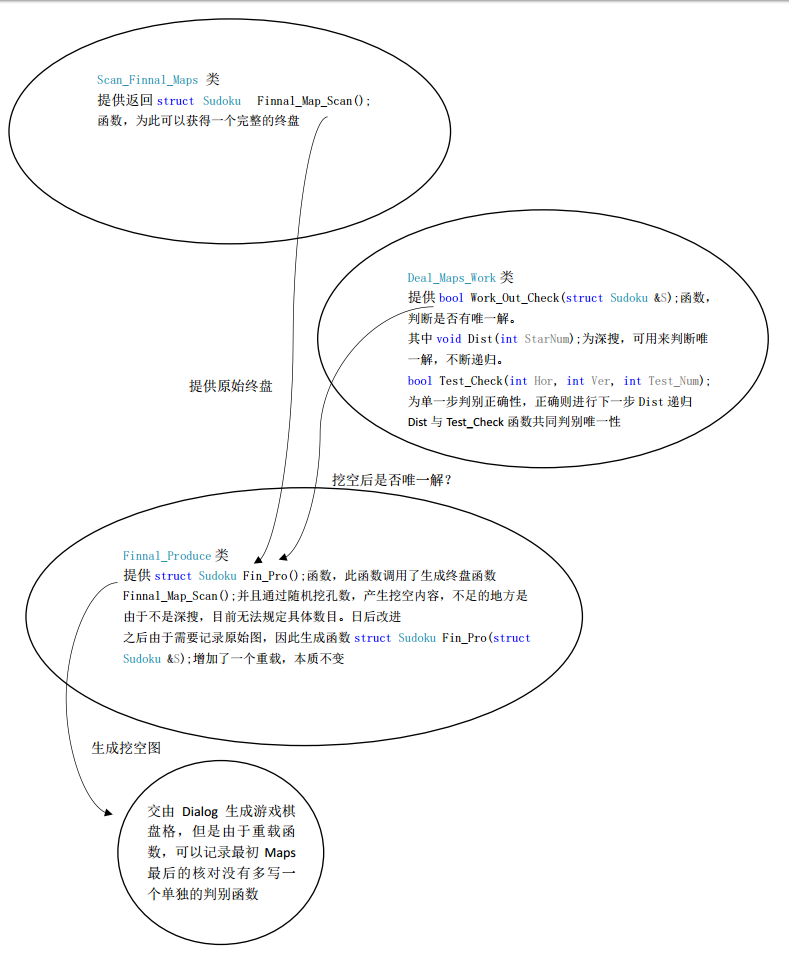
最后在这里讲一下，最后附加程序的制作实际上是先在一个工程里，通过调用输出自己的图，用0作为空，然后再重新建立dialog，重新复制一下类，然后制作成最后完整程序。

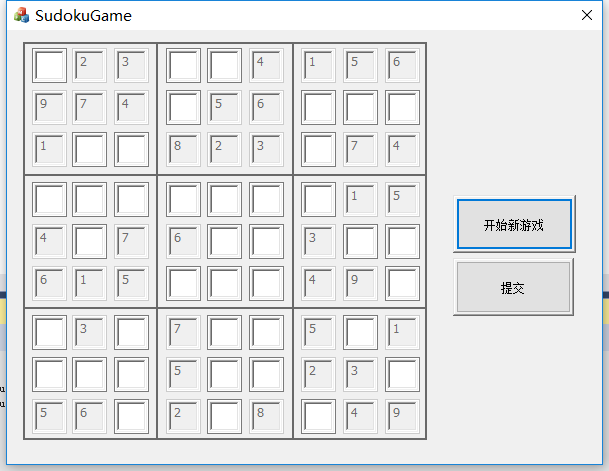
4>运行和效果图

基础程序在CMD中的运行测试

基础程序生成TXT文本

选做程序生成图

游戏成功（会数独同学的测试结果）

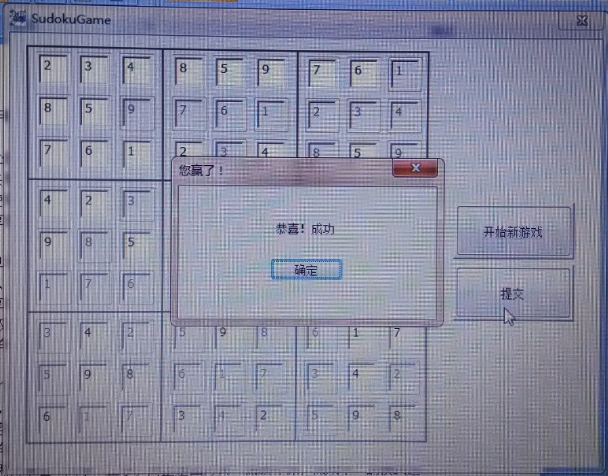
2、整体心路历程及新知呈现

1>第一次尝试

其实开始并没有按作业的拘束去做这件事，只是想着做一个随机生成的终盘，因为自己并不懂数独，甚至是完全没有接触过，我开始以为只需要判定在横、竖的行中，不存在重复的1-9即可，于是我开始写了自己的第一个数独程序，而且由于想要随机生成，就直接加上了很多的随机，开始打算一个位置一个位置随机，用两张棋盘格的图作为判定，来定位某一行某一列是否允许，如果不允许，那么就更换位置，而做着做着，除了随机难以把握控制以外，还有最后浇灭我想法的最后一个东西，那就是难以实现在重复后的递归偏移，以及转换。想了很久没有头绪，最后又由于没考虑到九个九宫格的关系，造成了自己直接放弃了这个想法。但是代码的内容留下了借鉴的之处。

2>第二、三次尝试

有了第一次失败的尝试，第二次就着重先看九个九宫格，通过一些资料的浏览，以及自己的发现，如果我找到第一行，分成三份，然后依次按顺序填入，然后在进行列的变换，这样就是一张完整的终盘了，但是开始的第一行，还是随机进行的。我发现这是可行的，于是开始了第一次成功的尝试，将随机第一行，以及各种矩阵变换进行应用。有了我第一个成品，即可以随机生成一个正确的终盘，但很快就出现一个问题，因为随机的原因，造成了程序无法生成不重复的终图，而改进它的措施，我给出的是，在原程序的基础上进行判别，然后如果重复就再随机生成一个新的再查重，于是有了我的一个自检函数及其所需的几个函数的第三次尝试

bool Map_isRep(struct Sudoku First, struct Sudoku Second);

void Error_Check(int i, struct Sudoku *p);

Sudoku ReBuild();

void Finnal_Check(int n,struct Sudoku S[])

其中Finnal_Check为主函数提供检测工作，有其他三个函数为其提供支持。另外，根据第一次尝试还有整个图的Check函数，我目前把他放到了百度云上，PS：（百度云链接）虽然他并没有能成为最后我的程序的源代码，但是为我后续的查重测试提供了很多帮助。同时我还因此学到了一个新知识。这个知识就是如何处理默认的递归工作栈，由于自己的函数，是一个不断递归的过程，由于100000个数据，一次重复消耗极大，而且重复的次数是随机的，其本身需要大量的栈空间，而默认的栈空间只有1M大小，于是在Running的时候，无限报错。十分头大后通过测试才发现，100 1000 10000 100000的数据量的数据重复数，如下图所示

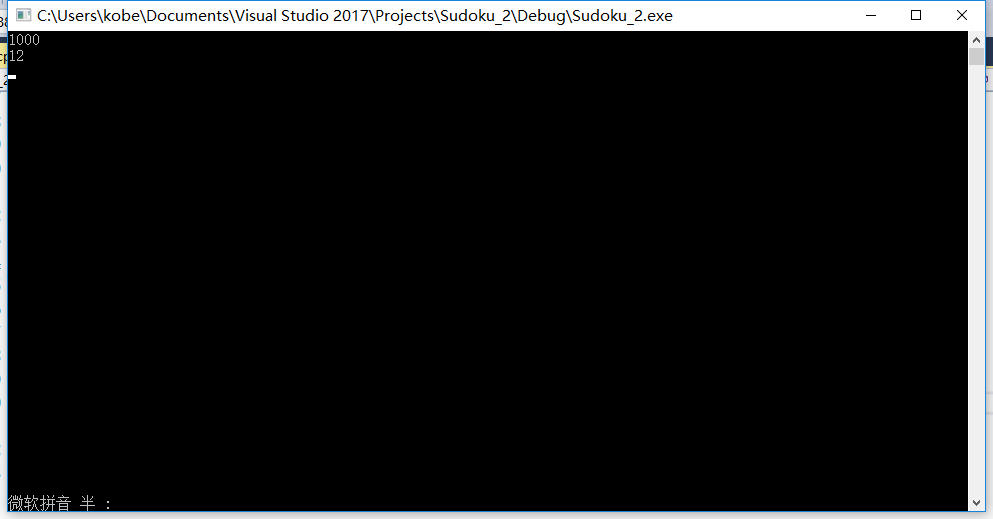
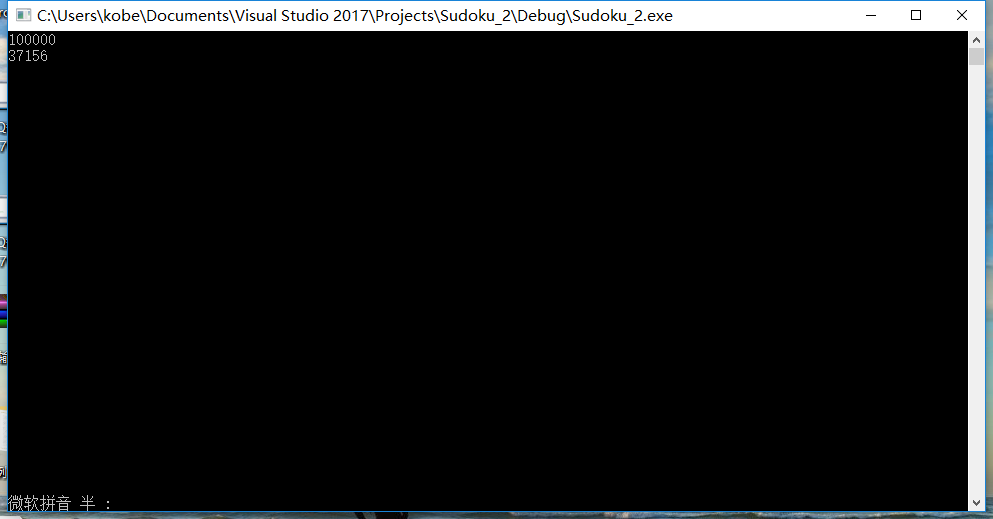
随机坑人，但是100000里有37000多的重复次数！这要是改，得改到什么时候，需要多大的空间，我于是改了默认栈大小如下

最后修改，重新随机生成不重复的100000数据，耗费了10多分钟，并且递归栈使用了500多M的空间。难以想象，但是的确，这个项目完成了。其衍生的重复计数函数，也成为了自己的一项工具。

3>第四次尝试

显然，如果我这样交上去，估计测试的助教学长，或者老师肯定会爆炸的。人不能任性，所以程序更应该不反人类才对嘛，于是就重新打鼓另开张，撤换掉随机功能，引入了一个全排列的STL库函数，并在外部现行做一个测试。让其能够为我所用。代码其实已经在上面了，下面我来讲讲他让我抓狂的一点，这个函数开始在测试时候，输入了1 2 3 4 5 6 7 8 9，一切运转正常，但是如果你输入7 1 2进行三个全排列的时候，你可能会爆炸，因为他执行两遍就停了，（num，num+3）无法让他得到6个不同的结果，究其原因，是因为其会从num[0]开始，next_permutation这个东西，只能是将num[0],找到下一个，7这个数字已经很大了，相当于执行的第四个，因此他之后只有两个排列。所以为保证你不知道这三个数是多少的时候，你需要进行一次排序，将其从小到大装入数组。
程序运行后的自检结果，至此，基础作业，Finnished！

4>GUI及多类分制的面向对象

得幸面向对象计算器的实践，以及自己最初函数的封装，多类分制在我这里只是简单的复制粘贴。

得到以上的.h和.cpp，通过main的运行，可以生成挖空所需的图

4>MFC制作

MFC只是多了几个对话框的.h .cpp以及调用他们的方式。
主要学会了加一个ICON等一些操作吧，给自己的程序设计了一些图标，至于MFC一些高级操作的的话，自己没有系统学习，只是需要什么不会了，就上百度，比如在MFC划线，CSDN的大佬交会了我用Picture Control重合来做，哈哈哈，小技巧很多，慢慢学，不一定记得住，但是百度，谷歌总会告诉我的~

5>章末总结

这次作业总共制作了一下几个工程，用于尝试，调试，以及最后实践

分别对应

1-4次尝试对应Sudoku_(1-4)
Sudoku_Finnal对应面向对象
SudokuGame对应最终程序
Sudoku_Borning对应挖空函数类
Next_Per_Test对应STL库函数测试

3、效能分析与构建之法和图表

1>单元测试及代码覆盖率

1）本次测试的代码，是最终生成了挖空版的数独文件，测试工具：C++ Coverage Validator（注：VS2017 专业版可能需要进行批处理操作才可以得到代码覆盖率结果，否则的单元测试结果文件无法导出。附：学长的教程）
2）本次类共有以上介绍的：Scan_Finnal_Maps类，Deal_Maps_Work类，Finnal_Produce类，main函数
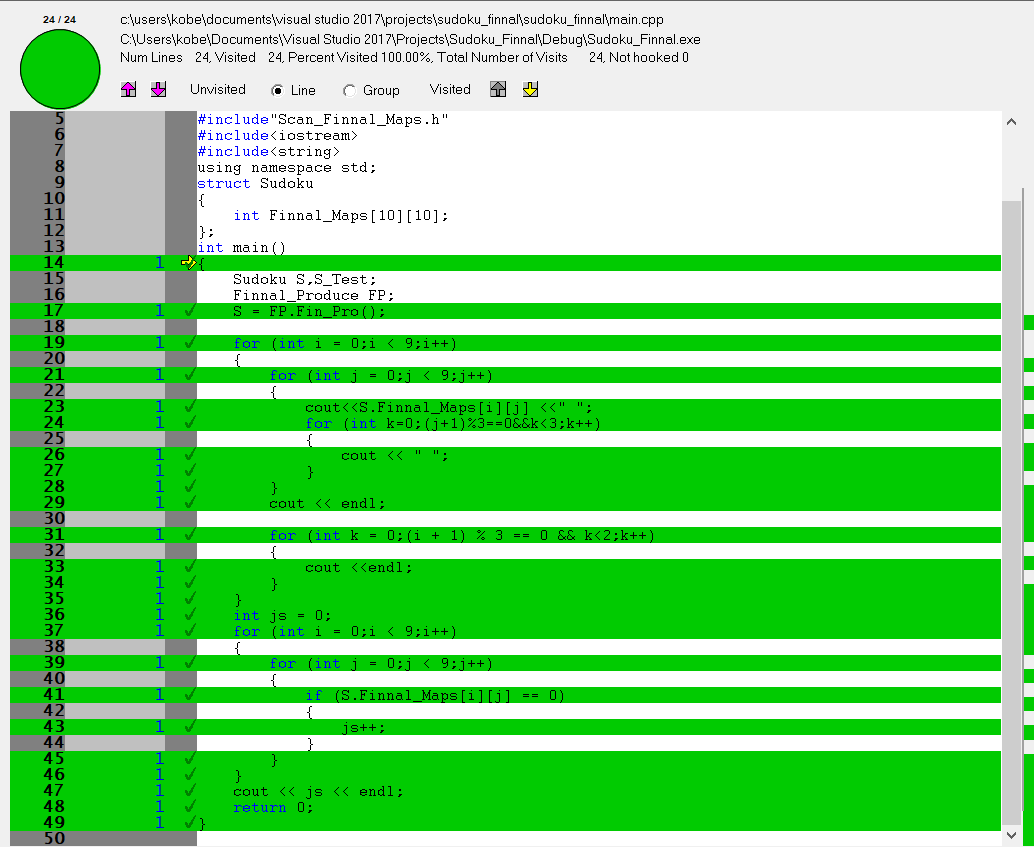
3）总体代码覆盖率结果如下图

4）由此看出其中只有图生成函数存在问题，细节如下

分析一下可以得到这个判断，是增加随机性的，在生成一次挖空终图的结果时，随机带有任意性，因此没有被覆盖。
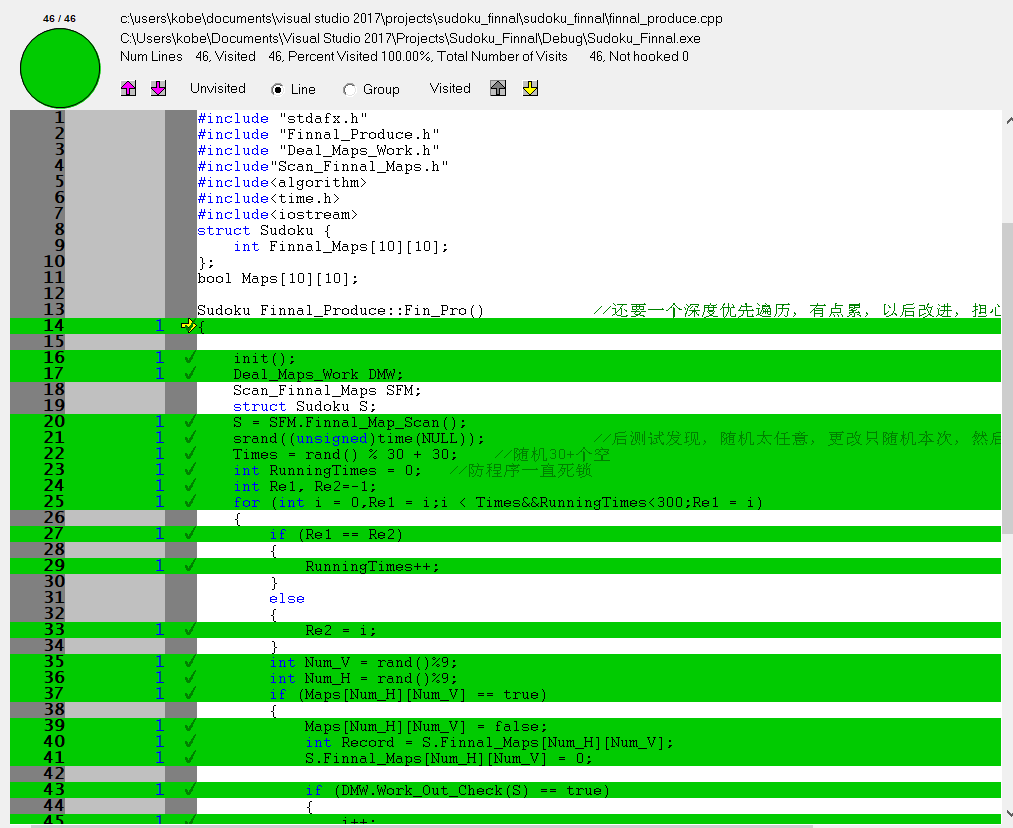
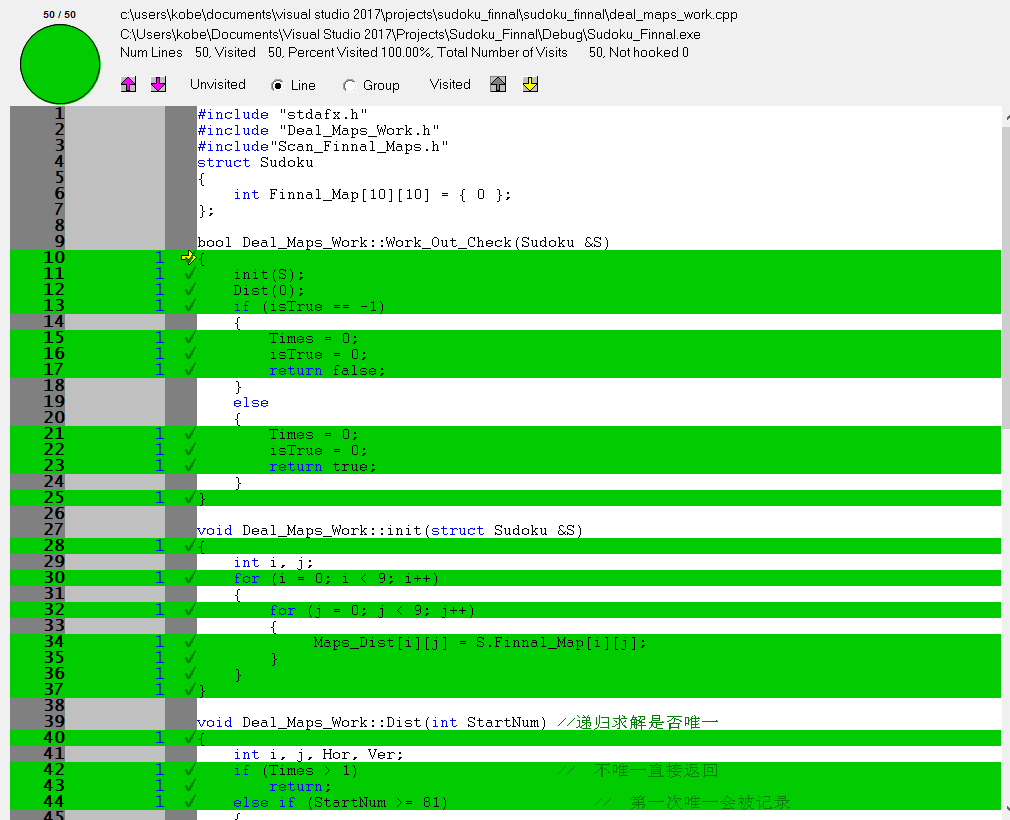
5）其他图代码覆盖率一览
main.cpp

Finnal_Produce类

Deal_Maps_Work类

总结

删除一些不必要的未覆盖的内容，将会增加算法的执行性能

2>性能分析

1）以模块参考，函数的调用关系的性能

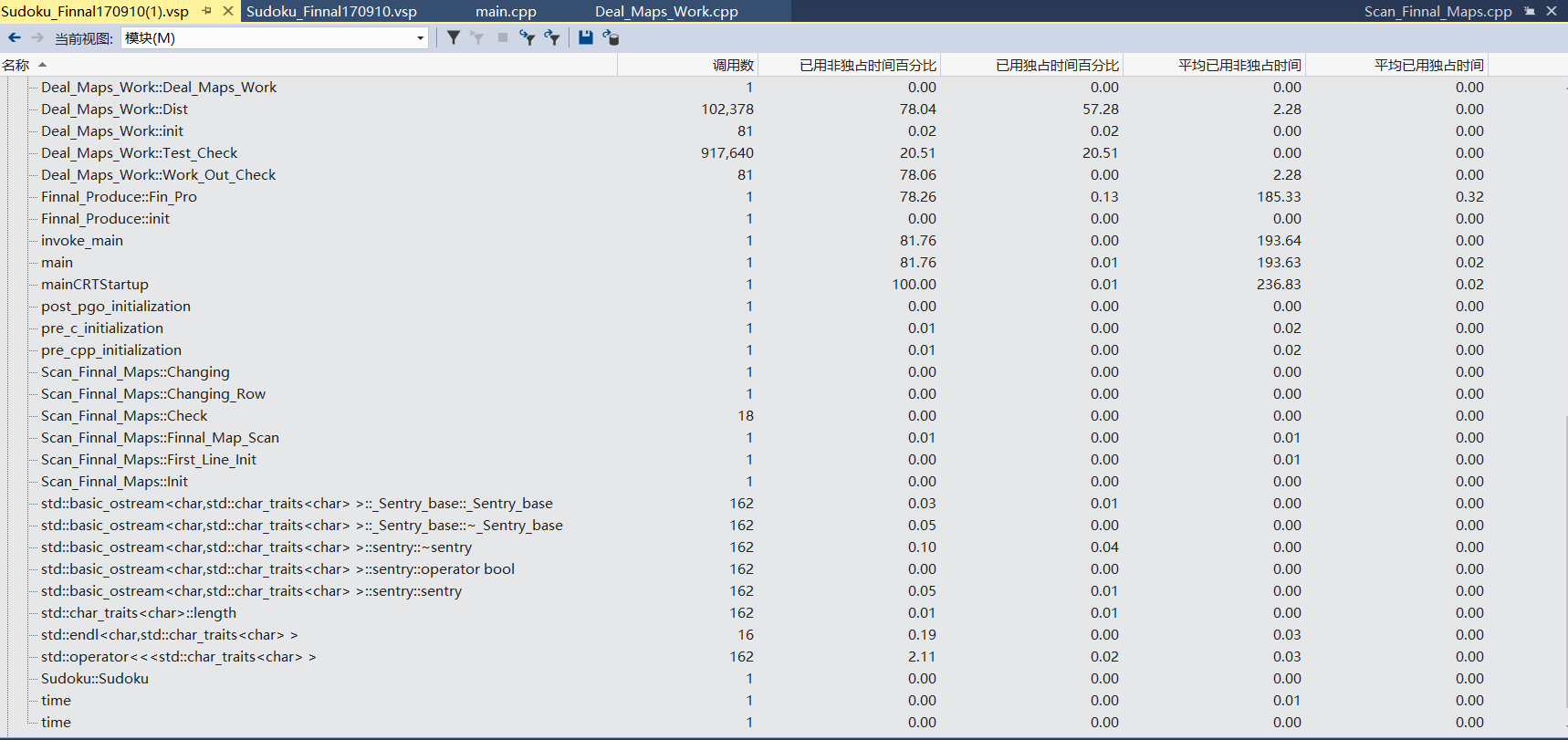
2）各类中函数调用占比概览
由于判定每一个空是否为唯一解，因此每一个空都需要一遍深度遍历，所以Work_Out_Check调用次数最多。

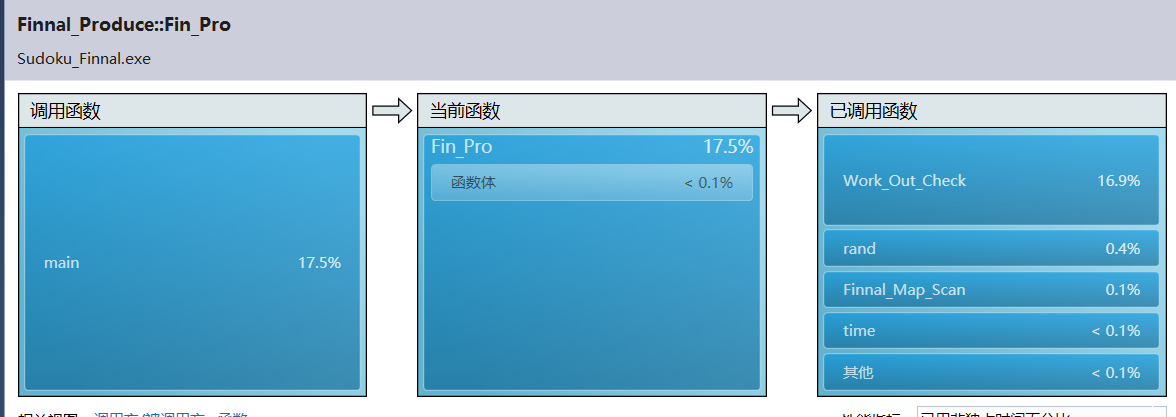
其次，Work_Out_Check中的dist为支持函数，因此递归同样需要。

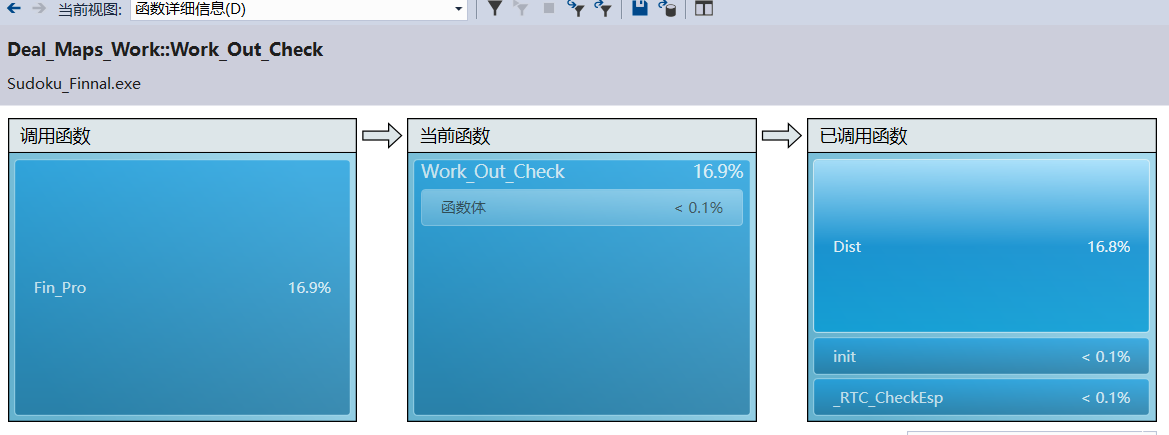
进一步地同步支持函数Test_Check

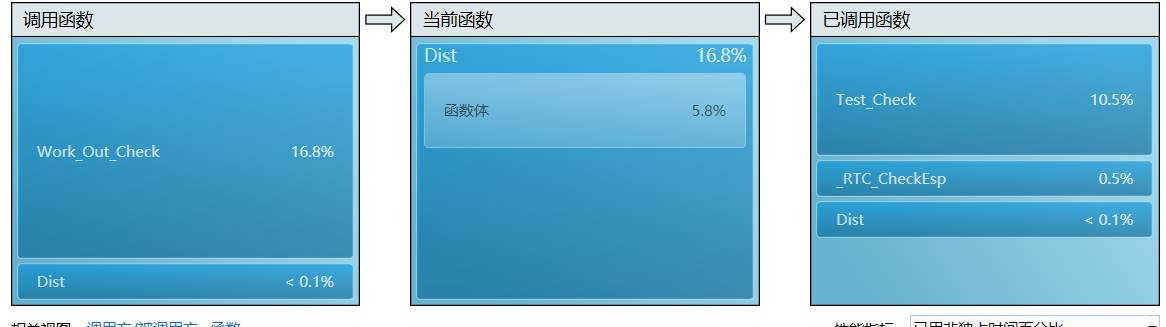
最后看一下生成图类中的情况

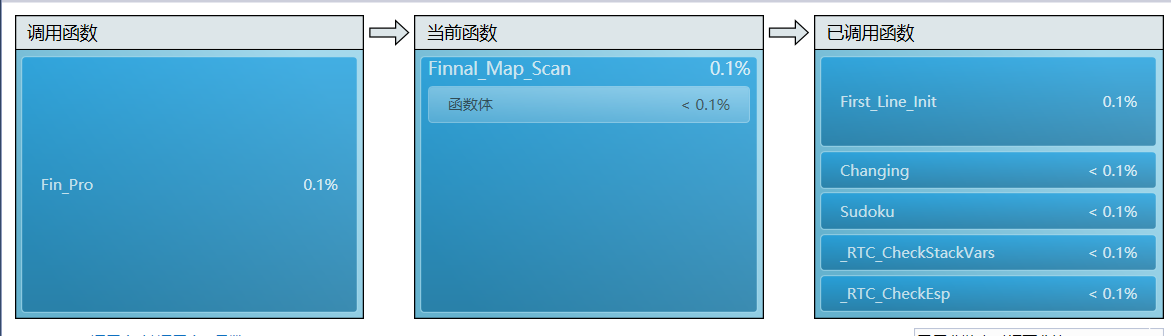
总结：

由此可以得出其限制本程序的瓶颈在于最后的挖空函数，而挖空函数取决于搜索和提供挖空数量的函数，对于搜索的情况，如果可以进一步增加搜索的效率则会提升本程序的执行效率，而对于最终的挖空数量而言，需要更加细致化。

2>《构建之法》启示

1）一个项目起始都是一个小的需求，由一个小的需求增加一些条件变成一个大的需求，然后不断扩展其功能，其中一个例子，从一个制造加法的功能，到加、减、乘、除，再到要求不重复，再到做成一个网站……这一系列的过程，让我明白，一个项目起源于一个需求，从需求入手，到用开发工具构建一个平台，将这个平台展示在人们面前，实现他们需求，这就是一个项目。这也是从宏观角度来讲述一个项目的制作过程。
2）一个软件，由程序和软件工程组成，而程序的开发，需要一个程序员由简单到复杂的过程，对于这个项目而言，模型的实现来讲，我实现的过程就是从构造一个终盘开始，到构造出4万个终盘，到构造6x4万，再构造216x4万，这个过程我认为是符合这个规律的。如果开始就想构造大量的数据，没有一个合理的规划，这样往往会出问题，也就是《构建之法》指出的盲目扩张，一个功能也是如此，我的MFC界面功能很简单，只有简单的构造，提交，确定功能。而在实现这个功能之前，我是在程序确定可以生成一个挖空终盘之后才开始的。而同样，不急于盲目地加上比如：计时功能，排行榜功能，难易度功能……这些可以实现，但是一定要专精一方面，做完之后再去想想如何继续下面的操作，有一个调理，而不是凭空想象，否则将会主次不分，丢了西瓜捡芝麻。因此一定要规划好自己做一件事的过程，如同程序一样，不可随意地return，或者break。这是从微观细化的角度来讲一个项目的问题。
3）软工团队的重要性，对于个人项目，那么一个人就好比一个项目，而对于团队项目，一个人好比一个项目里的一个类，你或许需要提供“界面接口”，“结果接口”，“输出接口”……而不同于各个接口，团队需要是一个个人，因此在内部，需要一个团队内部，交流通畅，按时交付，精确分工，个人投入，流程规划，准备到位，理性合作。这也是我期待的软工团队。虽然我个人实力不强，可能程序的算法没有那么优化，但是我觉得一个团队给我们的是挑战创意，挑战分工，挑战统筹，挑战合作的舞台，我认为这个舞台一定会有我们的一席之地。
4）关于单元测试和代码覆盖率，这是检验一个程序执行是否冗余，是否繁杂的一个很好的工具，对于这个新鲜的事物，我觉得自己还需要慢慢认识它，就如同当时的C++面向对象一样，对我而言一无所知，慢慢才了解到一个函数的工具作用。目前还不能熟练地运用，但之后会用好的。

3>图表

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	30	30
· Estimate	· 估计这个任务需要多少时间	30	30
Development	开发	1140	1410-1590
· Analysis	· 需求分析 (包括学习新技术)	120	60
· Design Spec	· 生成设计文档	120	180
· Design Review	· 设计复审 (和同事审核设计文档)	30	30
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	60	30
· Design	· 具体设计	240	120
· Coding	· 具体编码	480	720-900
· Code Review	· 代码复审	30	30
· Test	· 测试（自我测试，修改代码，提交修改）	60	240
Reporting	报告	180	210
· Test Report	· 测试报告	60	120
· Size Measurement	· 计算工作量	60	60
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	30
合计		1350	1650-1830

4、一些心得体会

首先呢，先提点题外话，我得跟隔壁班的我柯道个谢，组原无论是理论课还是实验课，从头到尾，让我感觉都很nice，除了课上的知识，还教会了我在学习之中怎么玩，开放自己的思想，学问是严谨的，但学习可以是轻松的，报告的数据是客观的，但报告心得可以写的生动有趣。没有枯燥和乏味，虽然知识很难，手动滑稽。所以呢，我也很纠结选哪个老师的课，我也知道栋哥的C++不停留在理论，注重实践，真的能学会很多东西。最后呢，还是随着班里的大多数人，跟随了栋哥，抱团取暖嘛。但还是心心念着我柯的！
之后转入正题，其实说很简单，做却很难，即使在之前有C++的练习，即使之前有msysgit的上传经历，但是一码归一码，做起来仍需努力！很多地方包括细节的传参，包括怎么写.h关联，细到每一步的时候就会发现自己很多东西都忘了，东西还要一点点学，一点点找回来，多次重复记忆，才会有提高。但是有一项东西却是我感觉到真正提升的，那就是会用百度和Google，我不再一味得追着别人问，而是把这个异常抛给搜索引擎来找bug，改bug，或者用一个新的东西。我觉得这是一个大一、大二没有，或者不完全具有的东西。它的获得将会使自己的学习，完全交由自己掌握，在之后的JAVA+AS中，书本是一部分，搜索引擎也将占另一部分比重。因为他就是我写出每一行代码的iostream库，以及import接口吧！

更新日志：
9.8 22：23 发现了基础作业的一个小BUG，正在处理中。。。。
9.9 2：49 BUG已修复，最新版本代码经优化后，可以理论最高生成896万以上不重复的数独终盘，而本代码目前可观的数独不重复最高理论量为3456万以上，如果按上述方式，改变第三行，将第三行更加深入地写，则会在896万的基础上，再乘以216（题目限制首位，不固定还可以x9）
9.9 18：27 基础作业更新，模型更新，C++代码更新，正在准备做修正后更新GitHub
9.9 22：59 GitHub已更新
9.10 10：23 更新了部分图表
9.10 20：39 更新了图表，完善了效能分析，《构建之法》，图表模块，修改了Github的链接，以备检测。
9.16 21：57更新了输出函数瓶颈，完成了3秒输出100万
9.20 17:12 更改了文章中关于freopen的问题，详情马上写在评论下。也感谢K班助教的认真。

posted @ 2017-09-08 14:43 kobe96 阅读(766) 评论(5) 编辑收藏举报

刷新页面返回顶部

kobe96