6 信息的表示和处理_整数运算
有趣的现象：计算机里，两个正数相加会得出一个负数，两个负数相加得出一个正数。为什么呢？看完这章就理解了。
1 无符号数加法
无符号数加法的数学**：
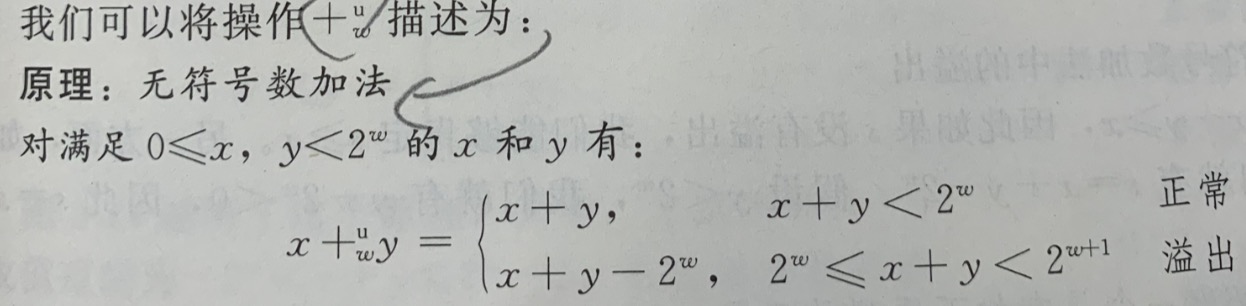
举例验证：
考虑一个4位数字的表示，x=9 和 y =12 的位表示分别是[1001]和[1100]，他们的和是21。5位的表示为[10101]。此时就发生溢出了。如果丢弃最高位，得到[0101]，即十进制的5。 5=9+12-2^4
等同于：
对于可以用x个位表示的两个无符号数，如果没有溢出，相加结果等于他们的和。如果有溢出，结果为两数之和减去2^x
在C中，无符号数相加，不会将溢出作为错误发出信号，需要自行判断是否溢出。
检测溢出：
两个无符号数相加，如果结果少于两个中较大的那个数，那就意味着发生了溢出。
2 补码加法
补码加法的数学推论：
解释下：
- 正溢出：正数相加，得到负数结果。
- 负溢出：负数相加，得到正数结果。
举例子验证：对于用4个位表示的两个有符号数：
| x | y | x+y | 截断后 | 溢出情况 |
|---|---|---|---|---|
| -8：[1000] | -5：[1011] | -13：[10011] | 3：[0011] | 负溢出 |
| -8：[1000] | -8：[1000] | -16：[10000] | 0：[0000] | 负溢出 |
| -8：[1000] | 5：[0101] | -3：[1101] | -3：[1101] | 正常 |
| 2：[0010] | 5：[0101] | 7：[0111] | 7：[0111] | 正常 |
| 5：[0101] | 5：[0101] | 10：[01010] | -6：[1010] | 正溢出 |
等同于：
对于可以用x个位表示的两个有符号数，相加后：
- 如果没有溢出，结果等于他们的和。
- 如果有正溢出，结果等于和减去2^x
- 如果有负溢出，结果等于和加上2^x
检测溢出：
- 正数相加，得到负数结果，表明发生正溢出
- 负数相加，得到正数结果，表明发生负溢出
4 阿尔贝群理论
因为阿尔贝群理论，我们可以得出：
- (x+y)-x ，求值总能得到y，无论加法是否溢出
- (x+y)-y，求值总能得到x，无论加法是否溢出
5 无符号数乘法
无符号数乘法的数学公式：
等同于：
对于可以用n个位表示的两个无符号数：x，y，相乘并对结果保留n位。那么这个截断后的值等于 【x乘以y，然后对2^n取模求余】。
补充说明：
- 任意两个可用x个位表示的无符号数想乘，结果的位数最多可能为2x位。 例如[110] * [110] = [100100]
- C语言中，无符号乘法并定义为产生x位的值，等于2x位的整数乘积的低x位表示的值。【就是截断只保留低x位并作为结果】
6 补码乘法
无符号数乘法的数学推论：
等同于：
对于可以用n个位表示的两个有符号数：x，y，相乘并对结果保留n位。那么这个截断后的值等于 【x乘以y，然后对2^n取模求余，然后将转为补码】
todo 有符号数乘法的二进制如何实现的
7 无/有符号数乘法验证
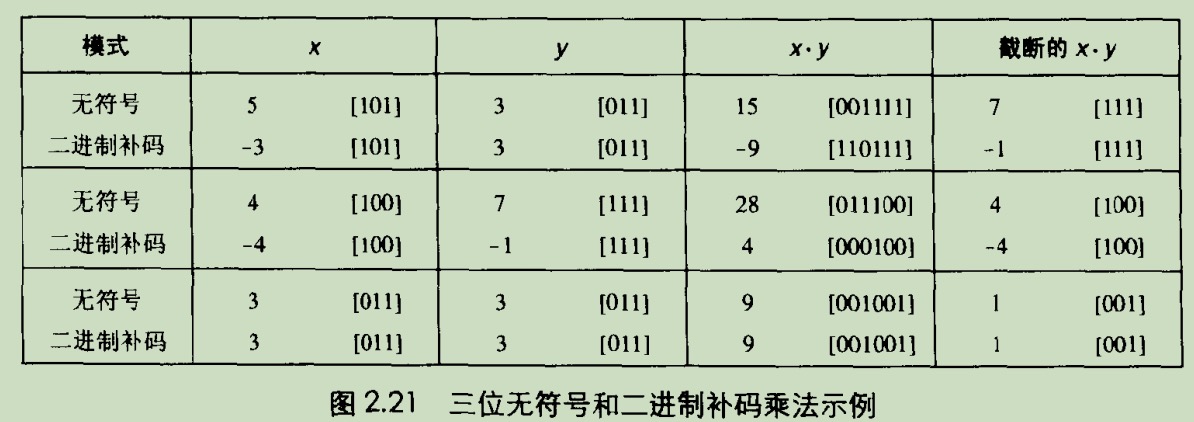
8 乘以常数
了解一下背景：
- 整数乘法、除法运算指令慢，需要耗费更多的时钟周期。慢
- 位运算需要耗费的始时钟周期少。快
- 用位运算和加法运算的组合来代替常数的乘法运算。左移
无符号数乘以2^n，等价左移n位
例如，假设一个程序包含表达式x*14。利用14=2³+2²+2¹，编译器会将乘法重写为 (x<<3)+(x<<2)+(x<<1)，将一个乘法替换为三个移位和两个加法。无论x是无符号的还是补码， 甚至当乘法会导致溢出时，两个计算都 会得到一样的结果
更好的是，编译器还可以利用属性14=24-21，将乘法重写为(x<<4)-(x<<1) ，这时只需要两个移位和一个减法。
9 除以2的幂
1、对于无符号数
数学推论：
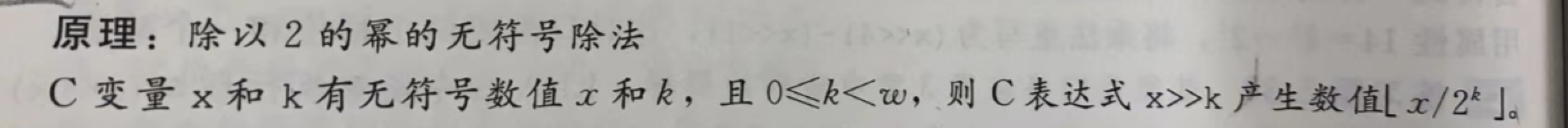
等同于：
无符号数用逻辑右移实现除以2^n。
验证：
16/2^2 =[0001 0000] >>>2 =[0000 0100] = 4
2、对于补码
数学推论：
等同于：
- 当补码为负数时，移位前加一个偏置(1<<k)-1，然后再进行算术右移
- 当补码是正数时，跟无符号数规则一致。
注意，除以2的幂我们可以通过逻辑或算术右移实现，但是与乘法不同，该方法不能推广到除以任意常数。
10 关于整数运算的最后思考
- 计算机执行的“整数”运算实际上是一种模运算形式。 改为【位运算】更容易理解
- 表示数字的有限字长限制了可能的值的取值范围，结果运算可能溢出。
- 补码表示提供了一种既能表示负数也能表示正数的灵活方法，同时使用了与执行无符号算术相同的位级实现，这些运算包括像加法、减法、乘法，甚至除法，无论运算数是以无符号形式还是以补码形式表示的，都有完全一样或者非常类似的位级行为。
- C语言中的某些规定可能会产生令人意想不到的结果，而这些结果可能是难以察觉或理解的缺陷的源头。【unsigned数据类型 很坑爹】
- 我们特别看到了unsigned数据类型，虽然它概念上很简单，但可能导致即使是资深程序员都意想不到的行为。我们还看到这种数据类型会以出意料的方式出现，比如，当书写整数常数和当调用库函数时。
11 阶段性总结
学习完 《4 信息的表示和处理_信息存储》、《5 信息的表示和处理_整数表示》《6 信息的表示和处理_整数运算》 这三节后，应该有以下的收获：
- 数据的表示、数据的运算的底层实现。
- 补码？因为有符号数的缺陷，引入了用补码来实现有符号数（正数或者负数）
- 为什么会产生溢出？因为字节数是固定的，比如只分配2个字节来存储整数，如果相加结果需要用3个字节才能存储，此时就会产生溢出
- 为什么两个正数相加的结果可能是负数？因为溢出，产生了截断。
