递归第二弹:分类强化
在递归第一弹里我介绍了递归的三种作用:
1.解决本来就是用递归形式定义的问题;
2.将问题分解为规模更小的子问题进行求解;
3.代替多重循环。
这篇文章举了一些例子以加深对递归的理解。
1.解决用递归形式定义的问题
之前说过,递归可以用来解决本来就是用递归形式定义的问题。那么什么叫用递归形式定义的问题呢?即定义概念的时候用到了定义自身,不过这个定义一定还会有一个不递归的定义作为终止条件。额......说起来好像有点绕,下面举几个栗子就知道了。
例题:逆波兰表达式
逆波兰表达式是一种把运算符前置的算术表达式(其实一般教科书上称这种表达式为波兰表达式),例如普通的表达式2 + 3的逆波兰表示法为+ 2 3。逆波兰表达式的优点是运算符之间不必有优先级关系,也不必用括号改变运算次序,例如(2 + 3) * 4的逆波兰表示法为* + 2 3 4。本题求解逆波兰表达式的值,其中运算符包括+ - * /四个。
输入
输入为一行,其中运算符和运算数之间都用空格分隔,运算数是浮点数
输出
输出为一行,表达式的值。
样例输入
* + 11.0 12.0 + 24.0 35.0
样例输出
1357.000000
提示: (11.0+12.0)*(24.0+35.0)
对本题中“逆波兰表达式”的定义:
1. 一个数是一个逆波兰表达式,值为该数
2. "运算符 逆波兰表达式 逆波兰表达式" 也是逆波兰表达式,值为两个逆波兰表达式的值运算的结果
在定义2中的逆波兰表达式中又用到了逆波兰表达式的定义,即递归定义。注意定义1不是递归的,它作为终止条件,否则定义会无限递归下去。根据逆波兰表达式的定义,如果读到的是一个运算符而不是数,后面势必还会有两个逆波兰表达式。将读到一个数的情况作为终止条件,避免无限递归。
根据定义写出的程序如下:
1 #include<iostream> 2 #include<stdlib.h> 3 #include<stdio.h> 4 using namespace std; 5 double exp() 6 { 7 char s[20]; 8 cin >> s;//每次读入一个字符串 9 switch(s[0]) 10 { 11 //读到运算符的情况 12 case '+':return exp()+exp(); 13 case '-':return exp()-exp(); 14 case '*':return exp()*exp(); 15 case '/':return exp()/exp(); 16 //读到数的情况 17 default:return atof(s);//终止条件 18 } 19 } 20 int main() 21 { 22 printf("%lf",exp()); 23 return 0; 24 }
输出结果如图(输入用空格分开):

再看一个递归定义的例子:四则运算表达式求值
输入为四则运算表达式,仅由整数、 +、-、 *、 / 、 (、 )组成,没有空格,要求求其值。假设运算符结果都是整数。 "/"结果也是整数
其中对表达式的定义为:
- 可以是一个单独的项
- 任意多个项相加减
对项的定义为:
- 可以是一个单独的因子
- 任意多个因子相乘除
对因子的定义为:
- (表达式)
- 整数
在表达式的定义中用到了项的定义,在项的定义中用到了因子的定义,在因子的定义中用到了表达式的定义,即递归定义。其中在因子定义中的一个整数就是一个因子是一个不递归的定义,即终止条件。
表达式定义的结构图如下:

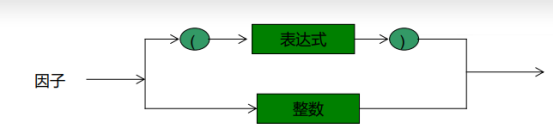
根据表达式的递归定义,对于表达式进行递归分析处理,程序如下:
1 #include<iostream> 2 #include<cstdlib> 3 using namespace std; 4 int factor_value(); 5 int term_value(); 6 int expression_value(); 7 int expression_value()//求一个表达式的值 8 { 9 int result = term_value();//先求第一项的值 10 bool flag = true;//查看是否还有其他项 11 while (flag) 12 { 13 char c = cin.peek();//查看输入流里的第一个字符,只看不取走 14 if (c == '+' || c == '-')//说明还有其他项 15 { 16 cin.get();//从输入中取走一个字符 17 //根据操作符进行相应的计算 18 if (c == '+') 19 { 20 result += term_value(); 21 } 22 else 23 { 24 result -= term_value(); 25 } 26 } 27 else//如果后面没有+或-,说明该表达式只有一项 28 { 29 flag = false;//相当于break; 30 } 31 } 32 return result; 33 } 34 35 int term_value()//求一项的值 36 { 37 int result = factor_value();//先求第一个因子的值 38 while (true) 39 { 40 char c = cin.peek();//查看输入流里的第一个字符,只看不取走 41 if (c == '*' || c == '/')//说明还有其他因子 42 { 43 cin.get();//取走这个操作符 44 //根据操作符进行相应的计算 45 if (c == '*') 46 { 47 result *= factor_value(); 48 } 49 else 50 { 51 result /= factor_value(); 52 } 53 } 54 else//如果后面没有+或-,说明该表达式只有一个因子 55 { 56 break; 57 } 58 } 59 return result; 60 } 61 62 int factor_value()//求一个因子的值 63 { 64 char c = cin.peek(); 65 int result = 0; 66 if (c != '(')//说明该因子为一个整数 67 { 68 while (isdigit(c))//当前为数字最高位 69 { 70 result = result * 10 + c - '0'; 71 cin.get(); 72 c = cin.peek(); 73 } 74 } 75 else//说明该因子为”(表达式)”的形式 76 { 77 cin.get(); 78 result = expression_value(); 79 cin.get(); 80 } 81 return result; 82 } 83 int main() 84 { 85 cout << expression_value() << endl; 86 system("pause"); 87 return 0; 88 }
输入结果如下图:
其实还有很多递归定义的问题,比如树的递归定义如下:
树(Tree)是n(n>=0)个结点的有限集。n=0时称为空树。在任意一颗非空树中:
1.有且仅有一个特定的称为根(root)的结点;
2.当n>1时,其余结点可分为m(m>0)个互补交互的有限集T1、T2...Tm,其中每一个集合本身又是一棵树,并称为根的子树(SubTree)。
这里子树的定义又用到了树的定义自身即递归定义,因此很多关于树的问题也是通过递归来解决的。
2.用递归将问题分解为规模更小的子问题进行求解
在求解原问题时,我们可以考虑是否能把原问题分解为与原问题形式相同,但是规模更小的子问题,通过子问题的解可以推出原问题的解。需要注意的地方是我们同样需要通过边界条件阻止无穷递归的发生。
例题: 爬楼梯
树老师爬楼梯,他可以每次走1级或者2级,输入楼梯的级数,求不同的走法数
例如:楼梯一共有3级,他可以每次都走一级,或者第一次走一级,第二次走两级,也可以第一次走两级,第二次走一级,一共3种方法。
输入
输入包含若干行,每行包含一个正整数N,代表楼梯级数, 1<= N <= 30输出不同的走法数,每一行输入对应一行
输出
不同的走法数,每一行输入对应一行输出
样例输入
5
8
10
样例输出
8
34
89
我们不妨先走第一步看看,由于每次只能走1级或者2级,如果第一步走了1级,那么剩下的问题就变成了如何走剩下额n-1级台阶;如果第一步走了2级,那么剩下的问题就变成了如何走剩下的n-2级台阶。即:n级台阶的走法 =先走一级后,n-1级台阶的走法+先走两级后,n-2级台阶的走法。若用一个函数f(n)表示走n级台阶的走法,那么问题可以表示为递推式f(n) = f(n-1)+f(n-2)。我们需要给这个递推式加上边界条件,避免无穷递归。边界条件的选取不唯一,只要可以阻止函数无穷递归即可。下面给出几种可行的边界条件:
边界条件:
1.n < 0时,f(n)=0;n= 0时,f(0)=1
由于参数每次都是减1或者减2,所以一定会到达小于0或者等于0的边界。当n<0时,即要走一个负数级的楼梯,显然没有这种走法,所以f(n)=0(n<1)。当n=0时,即要走0级楼梯的走法,站着不动就可以了(也算一种走法),所以f(0)=1。
2.n = 0时,f(0)=1;n= 1时,f(1)=1
对f(0)的取值前面已经解释过了,这里不再赘述。当n=1时,即走1级楼梯的走法,由于每次只能走1级或者2级,所以1级楼梯只有一种走法,即f(1)=1。
3.n = 1时,f(1)=1;n=2时,f(2)=2
由于每次只能走1级或者2级,所以2级楼梯有两种走法,两次都走1级楼梯或者一次走2级楼梯,即f(2)=2。
这里我用第二种情况作为边界条件,程序如下:
1 #include<iostream> 2 #include<stdlib.h> 3 using namespace std; 4 int f(int n) 5 { 6 if (n == 0 || n == 1) 7 return 1; 8 else 9 { 10 return f(n - 1) + f(n - 2); 11 } 12 } 13 int main() 14 { 15 int n; 16 while (cin >> n) 17 { 18 cout << "走" << n << "级楼梯数的方案为:"; 19 cout << f(n) << endl; 20 } 21 system("pause"); 22 return 0; 23 }
输出结果如下:

例题:放苹果
把M个同样的苹果放在N个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法? 5, 1, 1和1, 5, 1 是同一种分法。
输入
第一行是测试数据的数目t( 0 <= t <= 20)。以下每行均包含二个整数M和N,以空格分开。 1<=M, N<=10。
输出
对输入的每组数据M和N,用一行输出相应的K。
样例输入
1
7 3
样例输出
8
我们可以设i个苹果放在k个盘子里放法总数是 f(i,k),有下面两种情况:
一、k > i ,即盘子数量比苹果多,那么至少会有k-i个空盘,由于不考虑放苹果的顺序,所以我们不用关心具体哪几个盘子是空的。在有空盘的情况放求i个苹果的放法,其实就是求把i个苹果放到i个盘子上的放法,即 f(i,k) = f(i,i)。
二、k <= i 时,即盘子数量不比苹果多,那么总放法 可以分为两种:1.有盘子为空的放法;2.没盘子为空的放法。
我们分情况讨论:
1.有盘子为空的放法:有盘子为空,即有大于1个空盘,把i个苹果放在至少有1个空盘的k个盘子上的方法和把i个苹果放在有k-1个盘子的方法是一样的(其他盘子都确定了,最后一个空盘当然也就确定了)。
如果这k个盘子只有一个空盘,那剩下的问题就是求把i个苹果放在无空盘的k-1个盘子上的放法,即情况2。如果k个盘子有大于1个空盘,那么剩下的问题变成求把i个苹果放在k-1个至少有1个空盘上的方法,又变成了情况1,只是规模更小了,即求f(i,k-1) 。
2.没盘子为空的方法:没有空盘子,意味着每个盘子上至少会放一个苹果,那问题就变成了当求每个盘子上都放一个苹果后,i-k个苹果放在k个盘子上的方法,即求f(i-k,k)。
综上所述,k<=i时,总放法=有盘子为空的放法+没盘子为空的方法,即f(i,k) = f(i,k-1) + f(i-k,k)。
下面讨论一下边界问题,以下两种边界应该是比较容易想到的:
1.没有盘子可以放:不管手里有多少苹果,没有盘子的放法都为0,即k=0时,f(i,0)=0。
2.有盘子但没有苹果:没有苹果的放法是每个盘子都不放,放法为1,即i=0时,f(0,k)=1。
边界条件的设立的作用是避免无穷递归,也就是我们需要在递归进行到某些特殊时刻的时候,设立一块“挡板”把它给“挡住”,不让它有继续递归下去的可能。从上面的分析可以看出来f(i,k)只会有这两个变化方向:
1.k > i时,f(i,k) = f(i,i);
2.k <= i时,f(i,k) = f(i,k-1) + f(i-k,k)
我们来分析一下我们对之前对边界条件的设立到底能不能避免无穷递归:
当k>i时,返回f(i,i),即i=k,跳到2。
当k<=i时,i和k的变化是要不i每次-k,要不k每次-1。根据题意k≥0且k每次-1,那么k一定会到达临界点k=0。由于k<=i,因此i-k总是大于等于0的,因此i也一定会到达临界点i=0。
程序如下:
1 #include<iostream> 2 #include<stdlib.h> 3 using namespace std; 4 int f(int m, int n) 5 { 6 if (m < n) 7 { 8 return f(m,m); 9 } 10 if (m == 0) 11 { 12 return 1; 13 } 14 if (n == 0) 15 { 16 return 0; 17 } 18 return f(m, n - 1) + f(m - n, n); 19 } 20 int main() 21 { 22 int m, n, t; 23 cin >> t ; 24 while (t--) 25 { 26 cin >> m >> n; 27 cout << f(m, n) << endl; 28 } 29 system("pause"); 30 return 0; 31 }
输出结果如下:

例题:算24
1 #include<iostream> 2 #include<cmath> 3 #include<cstdlib> 4 using namespace std; 5 int const eps = 1e-6;//精度判断 6 double a[5];//存放要判断的四个数,由于有除法,可能有分数,所以用double 7 bool count24(double a[],int n)//判断a数组里的前n个数是否能构成24 8 { 9 if (n == 1)//边界条件:如果只有一个数,直接判断这个数是否等于24 10 { 11 if (fabs(a[0] - 24) <= eps) 12 { 13 return true; 14 } 15 else 16 return false; 17 } 18 else//如果不止一个数,就选两个数枚举所有可能的计算方式,把算出来的结果作为新数放进b[],计算count24(b,n-1) 19 { 20 double b[5]; 21 //枚举所有可能的两个数 22 for(int i = 0;i<n-1;++i) 23 for (int j = i + 1; j < n; ++j) 24 { 25 int m = 0;//记录当前b数组的元素个数 26 for (int k = 0; k < n; ++k) 27 { 28 if (k != j && k != i)//不是选中的两个数 29 { 30 b[m++] = a[k]; 31 } 32 } 33 //枚举所有可能的计算方式看是否能构成24 34 b[m] = a[i] + a[j]; 35 if (count24(b, m + 1))//m+1=n-1 36 { 37 return true; 38 } 39 b[m] = a[i] - a[j]; 40 if (count24(b, m + 1)) 41 { 42 return true; 43 } 44 b[m] = a[j] - a[i]; 45 if (count24(b, m + 1)) 46 { 47 return true; 48 } 49 b[m] = a[j] * a[i]; 50 if (count24(b, m + 1)) 51 { 52 return true; 53 } 54 //除法可能出现分母=0的情况 55 if (fabs(a[i] - 0) > eps)//分母不为0 56 { 57 b[m] = a[j] / a[i]; 58 if (count24(b, m + 1)) 59 { 60 return true; 61 } 62 } 63 if (fabs(a[j] - 0) > eps) 64 { 65 b[m] = a[i] / a[j]; 66 if (count24(b, m + 1)) 67 { 68 return true; 69 } 70 } 71 } 72 } 73 return false; 74 } 75 int main() 76 { 77 while (true) 78 { 79 for (int i = 0; i < 4; ++i) 80 { 81 cin >> a[i]; 82 } 83 if (a[0] == 0 && a[1] == 0 && a[2] == 0 && a[3] == 0) 84 { 85 break; 86 } 87 bool result = count24(a, 4); 88 if (result) 89 { 90 cout << "YES" << endl; 91 } 92 else 93 { 94 cout << "NO" << endl; 95 } 96 } 97 system("pause"); 98 return 0; 99 }



