最小生成树-Prim算法

一、基本概念

1.连通图：在无向图中，若任意两个顶点都有路径相通，则称该无向图为连通图。

2.连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。

3.生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。

4.最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。 

二、prim算法

• 基本思想: 

取图中任意一个顶点 v 作为生成树的根，之后往生成树上添加新的顶点 w。在添加的顶点 w 和已经在生成树上的顶点v 之间必定存在一条边，并且该边的权值在所有连通顶点 v 和 w 之间的边中取值最小。之后继续往生成树上添加顶点，直至生成树上含有 n 个顶点为止。 

 一般情况下所添加的顶点应满足下列条件:

在生成树的构造过程中，图中 n 个顶点分属两个集合：已落在生成树上的顶点集 U 和尚未落在生成树上的顶点集V-U ，则应在所有连通U中顶点和V-U中顶点的边中选取权值最小的边。

需要设一个辅助数组：

struct node{
　　VertexData AdjVertex;
　　int lowestcost;
}closedge[105];     

用下标表示未在生成树上的点，AdjVertex存储在生成树上的点，两点连成一个边，lowestcost表示权值，。最后得到的数组中存储的就是最小生成树的边。

• 过程图示：

 

 

 

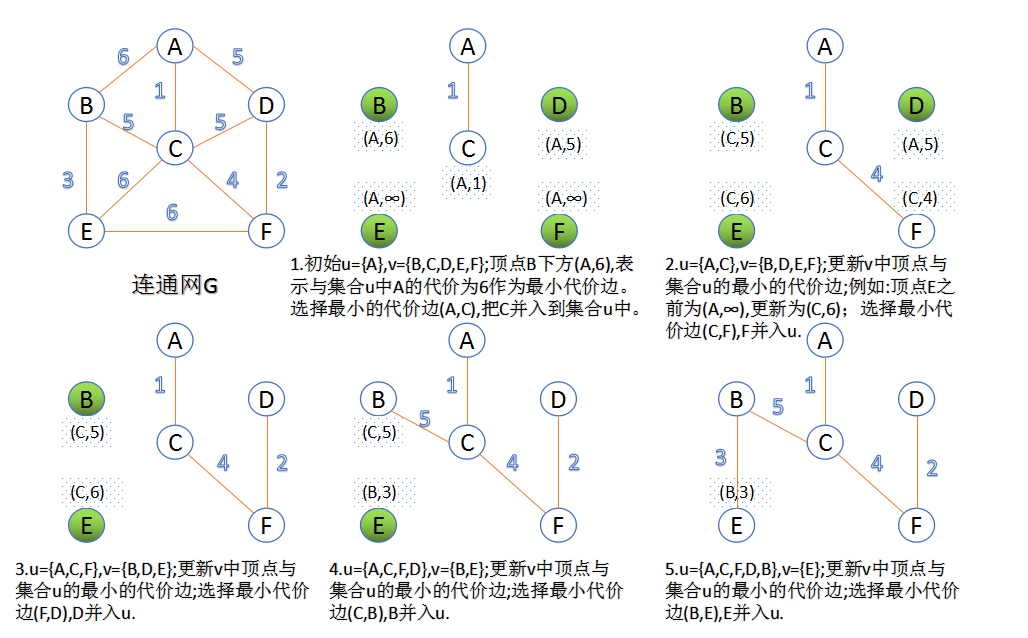
•  代码：

#include <bits/stdc++.h>

using namespace std;

#define VertexData int
#define INFINITE 1000000007

typedef struct{
    int AdjMatrix[105][105]; // 邻接矩阵
    int vertex_num; // 点的个数
    //int arc_num;
    //VertexData vertex[105];
}Graph;

struct node{
    VertexData AdjVertex; // 生成树中的点
    int lowestcost; // 权值
}closedge[105];
char vextex[] = { 'A', 'B', 'C', 'D', 'E', 'F' };

// 初始化邻接矩阵
void Build_Matrix(Graph *G) {
    for (int i = 0; i < G->vertex_num; i++)
        for (int j = 0; j < G->vertex_num; j++) {
            G->AdjMatrix[i][j] = INFINITE;
            G->AdjMatrix[j][i] = INFINITE;
        }
}

// 返回最小权值的边
int getmin(int n) {
    int Min = INFINITE;
    int index = -1;
    for(int i = 0; i < n; i++) {
        if(closedge[i].lowestcost && closedge[i].lowestcost < Min) {
            Min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}

// prim算法
void prim(Graph G, VertexData s) {
    // 初始化辅助数组
    for (int i = 0; i < G.vertex_num; i++) {
        closedge[i].lowestcost = INFINITE;
    }
    // 先存入起始点
    closedge[s].AdjVertex = s;
    closedge[s].lowestcost = 0;
    for(int i = 0; i < G.vertex_num; i++) {
        if(i != s) {
            closedge[i].AdjVertex = s;
            closedge[i].lowestcost = G.AdjMatrix[s][i];
        }
    }
    // 最多循环顶点个数n-1次
    for(int i = 0; i < G.vertex_num-1; i++) {
        int k = getmin(G.vertex_num);
        if(k == -1) break;
        cout << vextex[closedge[k].AdjVertex] << "--" << vextex[k] << endl;
        closedge[k].lowestcost = 0; // 权值赋0表示将该点并入最小生成树的集合
        // 更新树外最小代价边的信息
        for(int j = 0; j < G.vertex_num; j++) {
            if(G.AdjMatrix[k][j] < closedge[j].lowestcost) {
                closedge[j].lowestcost = G.AdjMatrix[k][j];
                closedge[j].AdjVertex = k;
            }
        }
    }
}

int main() {
    int m, n, a, b;
    Graph G;

    int ans = 0, cost, counter = 0;
    cout << "输入点个数" << endl;
    cin >> m;
    G.vertex_num = m;
    Build_Matrix(&G);
    cout << "输入边个数" << endl;
    cin >> n;
    cout << "输入边信息" << endl;
    for (int i = 0; i < n; i++) {
        cin >> a >> b >> cost;
        G.AdjMatrix[a][b] = cost;
        G.AdjMatrix[b][a] = cost;
    }
    prim(G, 0);
    return 0;
}


/*
 *

6
10
0 1 6
0 2 1
0 3 5
1 2 5
1 4 3
2 3 5
2 4 6
2 5 4
3 5 2
4 5 6
 * */
/*
    int locate(Graph G, char c) {
        for(int i = 0; i < G.vertex_num; i++) {
            if(G.vertex[i] == c)
                return i;
        }
        return -1;
    }
*/

 

三、例题

通畅工程：

Description

省政府“畅通工程”的目标是使全省任何两个村庄间都可以实现公路交通（但不一定有直接的公路相连，只要能间接通过公路可达即可）。经过调查评估，得到的统计表中列出了有可能建设公路的若干条道路的成本。现请你编写程序，计算出全省畅通需要的最低成本。 

 

Input

测试输入包含若干测试用例。每个测试用例的第1行给出评估的道路条数 N、村庄数目M ( < 100 )；随后的 N 
行对应村庄间道路的成本，每行给出一对正整数，分别是两个村庄的编号，以及此两村庄间道路的成本（也是正整数）。为简单起见，村庄从1到M编号。当N为0时，全部输入结束，相应的结果不要输出。 

 

Output

对每个测试用例，在1行里输出全省畅通需要的最低成本。若统计数据不足以保证畅通，则输出“?”。 

 

Sample Input

3 3 1 2 1 1 3 2 2 3 4 1 3 2 3 2 0 100

 

Sample Output

3 ?

 ac代码：

#include <bits/stdc++.h>

using namespace std;

#define VertexData int
#define INFINITE 10000000007

typedef struct{
    //VertexData vertex[1005];
    int AdjMatrix[105][105];
    //int arc_num;
    int vertex_num;
}Graph;

struct node{
    VertexData AdjVertex;
    int lowestcost;
}closedge[105];


void Build_Matrix(Graph *G) {
    for (int i = 0; i < G->vertex_num; i++)
        for (int j = 0; j < G->vertex_num; j++) {
            G->AdjMatrix[i][j] = INFINITE;
            G->AdjMatrix[j][i] = INFINITE;
        }
}

int getmin(struct node *closedge, int n) {
    int Min = INFINITE;
    int index = -1;
    for(int i = 0; i < n; i++) {
        if(closedge[i].lowestcost && closedge[i].lowestcost < Min) {
            Min = closedge[i].lowestcost;
            index = i;
        }
    }
    return index;
}

void prim(Graph G, VertexData s) {
    for (int i = 0; i < G.vertex_num; i++) {
        closedge[i].lowestcost = INFINITE;
    }
    closedge[s].AdjVertex = s;
    closedge[s].lowestcost = 0;
    for(int i = 0; i < G.vertex_num; i++) {
        if(i != s) {
            closedge[i].AdjVertex = s;
            closedge[i].lowestcost = G.AdjMatrix[s][i];
        }
    }
    for(int i = 0; i < G.vertex_num-1; i++) {
        int k = getmin(closedge, G.vertex_num);
        if(k == -1) break;
        closedge[k].lowestcost = 0;
        for(int j = 0; j < G.vertex_num; j++) {
            if(G.AdjMatrix[k][j] < closedge[j].lowestcost) {
                closedge[j].lowestcost = G.AdjMatrix[k][j];
                closedge[j].AdjVertex = k;
            }
        }
    }
}

int main() {
    int m, n, a, b;
    Graph G;
    while(~scanf("%d%d", &n, &m)) {
        if(!n) break;
        int ans = 0, cost, counter = 0;
        G.vertex_num = m;
        Build_Matrix(&G);
        for (int i = 0; i < n; i++) {
            cin >> a >> b >> cost;
            G.AdjMatrix[a-1][b-1] = cost;
            G.AdjMatrix[b-1][a-1] = cost;
        }

        prim(G, 0);
        for(int i = 1; i < m; i++) {
            if(closedge[i].lowestcost == 0) {
                ans += G.AdjMatrix[i][closedge[i].AdjVertex];
                counter++;
            }
        }
        if(counter != m-1)
            cout << "?" << endl;
        else
            cout << ans << endl;
    }
    return 0;
}

参考博客：https://blog.csdn.net/a2392008643/article/details/81781766