上一章先鸽子,全是天书
整除性
\[m|n \Rightarrow n=mk
\]
两个数的最大公因子是能整除它们两者的最大整数
\[gcd(n,m)=max\{k,k|m且k|n\}
\]
定义
\[gcd(0,n)=n
\]
最小公倍数
\[lcm(n,m)=min\{k,m|k且n|k\}=\frac{n*m}{gcd(n,m)}
\]
如果\(n\leq 0\)或\(m\leq 0\) 那么它没有定义
欧几里得算法:
\[gcd(0,n)=n\\
gcd(n,m)=gcd(n\ mod\ m,m),m>0
\]
证明式二:
\[只要证gcd(n,m)=gcd(n-m,m)\\
设gcd(n,m)=g\\
n=p*g\\
m=q*g\\
n-m=(p-q)*g\\
若gcd(q,p-q)=c\\
则q=k_1*c,p-q=k_2*c,p=(k_1+k_2)*c\\
因为gcd(p,q)=1\\
所以c=1
\]
推广,用它来计算满足
\[ax+by=gcd(x,y)
\]
的做法是,如果\(x=0\),就直接取\(a=0,b=1\),否则就令\(z=x\ mod\ y\),并用\(z\)和\(y\)替换\(x\)和\(y\)再次应用
\[by+cz=gcd(y,z)
\]
由于\(z=x-\lfloor\frac{x}{y}\rfloor y\)且\(gcd(y,z)=gcd(x,y)\),所以
\[by+c(x-\lfloor\frac{x}{y}\rfloor y)=gcd(x,y)\\
(b-\lfloor\frac{x}{y}\rfloor)y+cx=gcd(x,y)\\
a=b-\lfloor\frac{x}{y}\rfloor y,b=c
\]
小定理:
\[k|m,k|n\Leftrightarrow k|gcd(n,m)\\
\sum_{m|n}a_m=\sum_{m|n}a_{\frac{n}{m}}=\sum_{k}\sum_{m>0}a_m[n=mk]
\]
二重和式
\[\sum_{m|n}\sum_{k|m}a_{k,m}=\sum_{k|n}\sum_{l|(\frac{n}{k})}a_{k,kl}
\]
素数
任何正整数\(n\)都可以表示成素数的乘积
\[n=p_1…p_m=\sum_{i=1}^{k}p_k\ ,\ p_1\leq p_2\leq …\leq p_m
\]
次展开式是唯一的,仅有一种方式将\(n\)按照素数非减的次序写成素数的乘积,这个命题称为算术基本定理
证明略了
素数的例子
素数无限定理:
假设有\(k\)个素数,则\(M=p_1*p_2*…*p_k+1\)是素数
定义欧几里得数
\[e_k=e_1…e_{k-1}+1\\
gcd(e_n,e_m)=1\\
\]
用欧几里得算法易证,因为
\[e_n\ mod\ e_m=1\\
gcd(e_n,e_m)=gcd(1,e_m)=gcd(1,0)=1
\]
尝试将欧几里得数写成封闭形式,如果\(n>1\)
\[e_n=e_1…e_{n-2}*e_{n-1}+1=(e_{n-1}-1)e_{n-1}+1=e_{n-1}^2-e_{n-1}+1
\]
后面会证明,存在常数\(E≈1.264\),使得
\[e_n=\lfloor E^{2^n}+\frac{1}{2}\rfloor
\]
而只包含素数也有类似公式
\[p_n=\lfloor P^{3^{n}}\rfloor
\]
实际上它们不能称为封闭形式,因为常数\(E\)和\(P\)的来源不明
形如\(2^p-1\)的数称为梅森数
如果\(n\)是合数,则数\(2^{n}-1\)不可能是素数,因为\(2^{km}-1\)以\(2^m-1\)作为一个因子
\[2^{km}-1=(2^{m}-1)(2^{m(k-1)}+2^{m(k-2)}+…+1)
\]
但当\(p\)是素数时,\(2^p-1\)并不都是素数
\[P_n\sim nln(n)\\
\pi(x)\sim \frac{x}{ln(x)}
\]
\(\sim\)是渐进于,\(\pi(x)\)是\(x\)以内素数个数
\[ln(x)-\frac{3}{2}<\frac{x}{\pi(x)}<lnx-\frac{1}{2},x\geq67\\
n(ln(n)+lnln(n)-\frac{3}{2})<P_n<n(ln(n)+lnln(n)-\frac{1}{2}),x\geq 20
\]
观察一个随机整数\(n\),它是素数的机会大约是\(\frac{1}{n}\)
但素数分布不具有规律性,如孪生素数\(p\)和\(p+2\)的例子
阶乘的因子
\[n!=1*2*…*n=\prod_{k=1}^{n}k,整数n\geq 0
\]
利用第一章高斯的技巧,可以证明\(n!\)非常大
\[n!^2=(1*2*…*n)(n*…*2*1)=\prod_{k=1}^{n}k(n-k+1)
\]
我们有\(n\leq k(n+1-k)\leq \frac{1}{4}(n+1)^2\)
由于二次多项式\(k(n+1-k)=\frac{1}{4}(n+1)^2-(k-\frac{1}{2}(n+1))^2\)在\(k=1\)以及\(k=n\)时取最小值,在\(k=\frac{1}{2}(n+1)\)时取最大值,于是
\[\prod_{k=1}^{n}n!\leq n!^2\leq \prod_{k=1}^{n}\frac{(n+1)^2}{4}
\]
开方
\[n^{\frac{n}{2}}\leq n!\leq \frac{(n+1)^n}{2^n}
\]
阶乘以指数增长
有斯特林公式
\[n!\sim \sqrt{2\pi n}(\frac{n}{e})^n
\]
渐进误差约为\(\frac{1}{12n}\)
另一个问题:求能整除\(n!\)的\(p\)最大幂次,如\(p=2\)时
\[\varepsilon_2(n!)=\lfloor\frac{n}{2}\rfloor+\lfloor\frac{n}{4}\rfloor+…=\sum_{k\geq 1}\lfloor\frac{n}{2^k}\rfloor
\]
例如
\[\varepsilon_2(100!)=50+25+12+6+3+1
\]
每一项都是前一项的\(\lfloor\frac{1}{2}\rfloor\),从二进制很好看出规律
\[(1100100)_2=100\\
(110010)_2=50\\
(11001)_2=25\\
(1100)_2=12\\
(110)_2=6\\
(11)_2=3\\
(1)_2=1
\]
也表示出了另外的规律
\[\varepsilon_2(n!)=n-v_2(n)
\]
其中\(v_2(n)\)表示\(n\)的二进制中\(1\)的个数
推广到任意的素数\(p\)
\[\varepsilon_p(n!)=\lfloor\frac{n}{p}\rfloor+\lfloor\frac{n}{p^2}\rfloor+…=\sum_{k\geq 1}\lfloor\frac{n}{p^k}\rfloor
\]
\(\varepsilon_p(n!)\)有多大?在求和中直接去掉低,然后对无穷级数求和估计上界
\[\varepsilon_p(n!)<\frac{n}{p}+\frac{n}{p^2}+…\\
=\frac{n}{p}(1+\frac{1}{p}+…)\\
=\frac{n}{p}(\frac{p}{p-1})\\
\frac{n}{p-1}
\]
\(\varepsilon_p(n!)\)的界反过来会给出一个关于\(p^{\varepsilon_p(n!)}\)的界
\[p^{\varepsilon_p(n!)}<p^{\frac{n}{p-1}}
\]
因为\(p\leq 2^{p-1}\) ,我们可以放宽上界化简
\[p^{\frac{n}{p-1}}\leq (2^{p-1})^{\frac{n}{p-1}}=2^n
\]
得到结论,任何素数对\(n!\)的贡献都小于\(2^n\)
利用这个,我们可以得到另一个素数无限定理的证明:
如果只要\(k\)个素数,那么对所有\(n>1\)就会有\(n!<(2^n)^k=2^{nk}\),因为每一个素数最多贡献一个因子\(2^{n}-1\),但是又足够大的\(n\)使\(n!<2^{nk}\)矛盾
甚至能对这一证明方法加强得到\(\pi(n)\)的一个粗略的界,每一个这样的素数都对\(n!\)贡献一个小于\(2^n\)的因子,所以与前相同有
\[n!<2^{n\pi(n)}
\]
用斯特林近似代替\(n!\),并取对数
\[n\pi(n)>nlg(\frac{n}{e})+\frac{1}{2}lg(2\pi n)
\]
与\(\pi(n)\sim \frac{n}{lnn}\)相比,这个下界很弱
互素
\(gcd(n,m)=1\)时,整数\(m\)和\(n\)没有公共的素因子,我们就称它们是互素的,记作\(n⊥m\)
\[\frac{m}{gcd(n,m)}⊥\frac{n}{gcd(n,m)}
\]
可以用\(gcd(kn,km)=k*gcd(n,m)\)得到
有一种方法构造满足\(m⊥n\)的全部非负分数\(\frac{m}{n}\)组成的集合,它称为\(Stern-Brocot\)树,思想是从两个分数\((\frac{0}{1},\frac{1}{0})\)出发,然后依次重复:
在两个相邻的分数\(\frac{m}{n}\)和\(\frac{m'}{n'}\)之间插入\(\frac{m+m'}{n+n'}\),新的分数称为\(\frac{m}{n}\)和\(\frac{m'}{n'}\)的中位分数
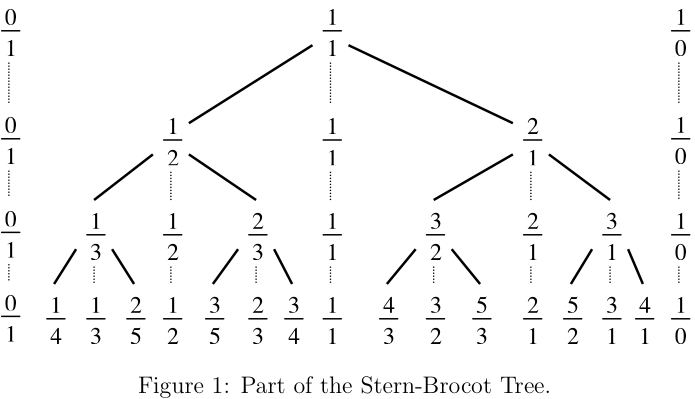
为什么每一个出现在树中的分数都是最简分数?为什么所有可能的分数\(\frac{m}{n}\)都刚好出现一次?
如果\(\frac{m}{n}\)和\(\frac{m'}{n'}\)是这个构造中任何一个阶段的相邻分数,我们就有
\[m'n-mn'=1
\]
这个关系开始时正确:
\(1*1-0*0=1\)
当新插入一个中位分数时,需要检验
\[(m+m')n-m(n+n')=1\\
m'(n+n')-(m+m')n'=1
\]
易证这两个等于都等价于它们替换的原始条件
由此证明了\(\frac{m+m'}{n+n'}\)是最简的


