汉诺塔
设\(T_n\)为\(n\)个圆盘的方案数，显然\(T_0=0,T_1=1\)
构造一种方案：将\(n-1\)个圆盘移动到第二根柱子上，将最大的圆盘移动到第三根柱子，再将\(n-1\)个圆盘移动过去
那么按照此方案至少有
\[T_n≤2T_{n-1}+1,n>0
\]
且易证最优
\[T_n≥2T_{n-1}+1,n>0
\]
所以
\[T_0=0,T_n=2T_{n-1}+1,n>0
\]
\(n\)很大时递归式不好算，考虑一个封闭形式
观察好像有
\[T_n=2^n-1
\]
至少\(T_1=2^1-1\)
那么当\(T_{n-1}=2^{n-1}-1\)时，有\(T_n=2T_{n-1}+1=2^n-1\)，根据归纳得\(T_n=2^n-1\)
有时我们观察不到\(T_n=2^n-1\)
也许更容易发现\(U_n=T_n+1=2^n\)
平面上的直线
求平面上\(n\)条直线所界定的区域的最大个数\(L_n\)
显然\(L_0=1，L_1=2,L_2=4\)
那么似乎有\(L_n=2^n\)
然后有\(L_3=7\)，What a pity
第\(n\)条直线使得区域增加\(k\)个，当且仅当对\(k\)个已有区域进行分割，即与已有直线有\(k-1\)个交点，此前仅有\(n-1\)条直线
\[L_n≤L_{n-1}+n,n>0
\]
易证等号可取（第\(n\)条与此前所有直线有交点可取）
\[L_0=1,L_n=L_{n-1}+n,n>0
\]
展开\(L_n\)得
\[L_n=L_0+1+2+3+…+n
\]
\[L_n=1+S_n
\]
\[S_n=1+2+3+…+n
\]
\(S_n\)又称三角形数，是一个有\(n\)行的三角形阵列中保龄球的个数
高斯九岁得出了计算\(S_n\)的办法
\[S_n=1+2+3+…+n
\]
\[S_n=n+(n-1)+(n-2)+…+1
\]
\[2S_n=(n+1)+(n+1)+…+(n+1)=n*(n+1)
\]
\[S_n=\frac{n*(n+1)}{2}
\]
由此得出
\[L_n=1+\frac{n*(n+1)}{2},n≥0
\]
归纳也可得
\[L_n=L_{n-1}+n=(\frac{(n-1)*n}{2}+1)+n=1+\frac{n*(n+1)}{2}
\]
问题变形：用折线代替直线，每个折线包含一个尖，求\(n\)条折线能界定的区域最大个数\(Z_n\)
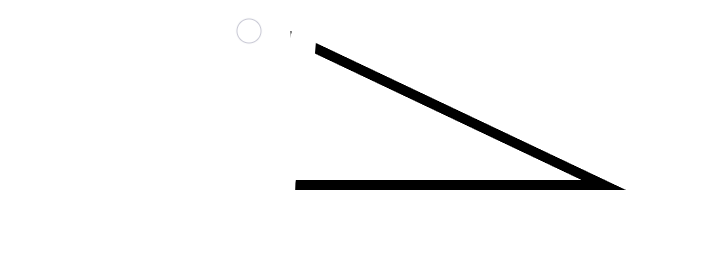
先列小数据：\(Z_0=1,Z_1=2,Z_2=7\)
观察发现（根本没法发现x）：一个折线相当于两条相交直线去掉一半（去掉蓝色一半）
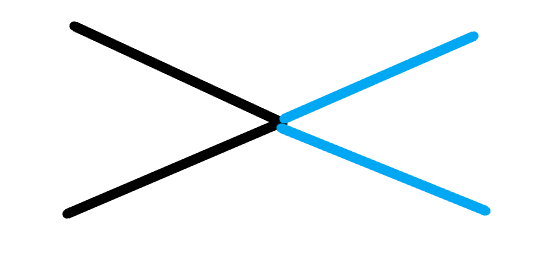
等价于：每条折线我们失去了两条直线界定空间中的两个，也就是
\[Z_n=L_{2n}-2n
\]
\[Z_n=2n^2-n+1,n≥0
\]
约瑟夫问题
\(n\)个人围成一个圆圈，隔一个杀一个，直到只有一人存活，求存活的人的编号
如\(n=10\)时，杀死的顺序是\(2、4、6、8、10、3、7、1、9\)
于是得到\(J(10)=5\)
猜测\(J(n)=\frac{n}{2}\)
然后试了几次就\(GG\)了
假设有\(2n\)个人，经过第一轮只剩下奇数编号的人，那么\(3\)号就成为下一个要离开的人
也就是除了每个人的号码加倍再减一，其他规则同\(n\)个人一致
那么\(J(2n)=2J(n)-1\)
由此\(J(20)=2*J(10)-1,n≥1\)
同理\(J(2n+1)=2J(n)+1\)
结合得到递推式
\[J(1)=1
\]
\[J(2n)=2J(n)-1,n≥1
\]
\[J(2n+1)=2J(n)+1，n≥1
\]
指数级的递推式更快捷
打表
\[J(1)=1
\]
\[J(2)=1,J(3)=3
\]
\[J(4)=1,J(5)=3,J(6)=5,J(7)=7
\]
\[J(8)=1,J(9)=3,J(10)=5,J(11)=7,J(12)=9,J(13)=11,J(14)=13,J(15)=15
\]
\[J(16)=1
\]
似乎可以按\(2\)的幂分组，并且每组开始\(J(n)=1\)
\[J(2^m+l)=2l+1,m≥0,0≤l<2^m
\]
对\(m\)归纳
\[J(1)=1,J(2^m+l)=2J(2^{m-1}+\frac{l}{2})-1=2(\frac{l}{2}+1)-1=2l+1
\]
观察前式可知
\[J(2n+1)-J(2n)=2
\]
拓展：
假设\(n\)的二进制展开式是
\[n=(b_mb_{m-1}…b_1b_0)_2
\]
等价于
\[n=b_m*2^m+b_{m-1}*2^{m-1}+…+b_1*2+b_0
\]
其中\(b_i=0\)或\(1\)，而首位\(b_m=1\)
那么依次有
\[n=(1b_{m-1}…b_1b_0)_2
\]
\[l=(0b_{m-1}…b_1b_0)_2
\]
\[2l=(b_{m-1}…b_1b_00)_2
\]
\[2l+1=(b_{m-1}…b_1b_01)_2
\]
\[J(n)=2l+1,J(n)=(b_{m-1}…b_1b_0b_m)_2
\]
最后得到了
\[J((b_mb_{m-1}…b_1b_0)_2)=(b_{m-1}…b_1b_0b_m)_2
\]
\(n\)向左循环一位就得到了\(J(n)\)
如果一直用二进制表示也许很快就能发现
根据循环可以期待进行\(m+1\)次迭代再次得到\(n\)
但事实上例如\(J((1101)_2)=(1011)_2\),再迭代一次\(J((1011)_2)=(111)_2\),当\(0\)为首位时会消失
实际上\(J(n)\)必然\(≤n\)，于是如果\(J(n)<n\)就不可能迭代回\(n\)
反复迭代得到一系列递减数列后最终会到达一个不动点\(J(n)=n\)（至少还有\(J(1)=1\)呢）
显然这个不动点的二进制表示中全是\(1\)
所以不动点的数值是\(2^{v(n)}-1\)，其中\(v(n)\)是\(n\)的二进制表示中\(1\)的个数
回去考虑第一个猜测：\(J(n)=\frac{n}{2}\)
考虑它什么时候成立
\[J(n)=\frac{n}{2}
\]
\[2l+1=\frac{2^m+l}{2}
\]
\[l=\frac{2^m-2}{3}
\]
当\(l=\frac{2^m-2}{3}\)为整数时，\(n=2^m+l\)就是一个解
不难验证，当\(m\)为奇数时，\(2^m-2\)是\(3\)的倍数，但当\(m\)为偶数时则不然（后面再研究）
前几个解：
\[m=1,l=0,n=2,J(n)=1,n=(10)_2
\]
\[m=3,l=2,n=10,J(n)=5,n=(1010)_2
\]
\[m=5,l=10,n=42,J(n)=21,n=(101010)_2
\]
\[m=7,l=42,n=170,J(n)=85,n=(10101010)_2
\]
其中通过二进制很好看出来
再拓展：
引入
\[f(1)=α,f(2n)=2f(n)+β,f(2n+1)=2f(n)+γ
\]
打表
\[f(1)=α
\]
\[f(2)=2α+β,f(3)=2α+γ
\]
\[f(4)=4α+3β,f(5)=4α+2β+γ,f(6)=4α+β+2γ,f(7)=4α+3γ
\]
\[f(8)=8α+7β,f(9)=8α+6β+γ
\]
一般地
\[f(n)=A(n)α+B(n)β+C(n)γ
\]
\[A(n)=2^m,B(n)=2^m-l-1,C(n)=l
\]
归纳法易证，但是很难直接得出此结论
下面考虑一般方法
令\(f(n)=A(n)\)，可得\(α=1,β=γ=0\)
\[A(n)=1,A(2n)=2A(n),A(2n+1)=2A(n)
\]
成立
若代入\(f(n)=1\)
\[1=α,1=2*1+β,1=2*1+γ
\]
此时\(α=1,β=γ=-1\)
类似，若代入\(f(n)=n\)，得到\(α=1,β=0,γ=1\)
但由此我们有
\[A(n)=2^m,A(n)-B(n)-C(n)=1,A(n)+C(n)=n
\]
\[C(n)=n-A(n)=l
\]
\[B(n)=A(n)-1-C(n)=2^m-1-l
\]
猜想的结果被完美推出
此为成套方法，有多少个独立参数就需多少独立特解
将成套方法用于约瑟夫问题：
已知
\[J((b_mb_{m-1}…b_1b_0)_2)=(b_{m-1}…b_1b_0b_m)_2
\]
若令\(β_0=β,β_1=γ\)
\[f(1)=α
\]
\[f(2n+j)=2f(n)+β_j，j=0,1,n≥1
\]
按二进制展开就是
\[f((b_mb_{m-1}…b_1b_0)_2)=2f((b_mb_{m-1}…b_1)_2)+β_{b_0}
\]
\[=4f((b_mb_{m-1}…b_2)_2)+2β_{b_1}+β_{b_0}
\]
\[=2^mα+2^{m-1}β_{b_{m-1}}+…+2β_{b_1}+β_{b_0}
\]
则有
\[f((b_mb_{m-1}…b_1b_0)_2)=(αb_{m-1}…b_1b_0)_2
\]
打表
\[f(1)=α
\]
\[f(2)=2α+β,f(3)=2α+γ
\]
\[f(4)=4α+2β+β,f(5)=4α+2β+γ,f(6)=4α+β+2γ,f(7)=4α+γ+2γ
\]
例如
\[n=100=(1100100)_2,α=1,β=-1，γ=1
\]
\[f(n)=64+32-16-8+4-2-1=73
\]
以\(100\)为例，\(1100100\)中每个\(1\)被\(0\)（\(-1\)）减至最靠右的\(0\)的位置上
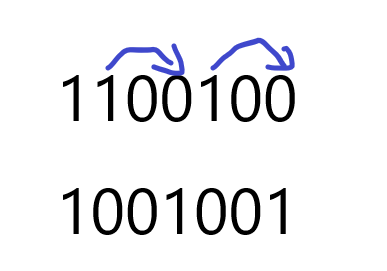
由此推出循环移位性质
更拓展：
\[f(j)=α_j,1≤j<d
\]
\[f(dn+j)=cf(n)+β_j，0≤j<d,n>0
\]
则有
\[f((b_mb_{m-1}…b_1b_0)_d)=(αb_{m-1}…b_1b_0)_c
\]
例如假设
\[f(1)=34,f(2)=5,f(3n)=10f(n)+76,n>0,f(3n+1)=10f(n)-2,n>0,f(3n+2)=10f(n)+8,n>0
\]
有\(d=3,c=10\)，要求\(d=19\)
则
\[f(19)=f((201)_3)=(5,76,-2)_{10}=5*100+76*10-2=1258
\]
约瑟夫问题有趣起来了
习题
1.当\(n=2\)时，\(1\)到\(n-1\)与\(2\)到\(n\)不存在交叉部分，不具有传递性
\[T_0=0,T_1=2
\]
\[T_n=3T_{n-1}+2
\]
\[T_n=3^n-1
\]
3.显然
4.数学归纳法
\(n=1\)时，移动次数为\(0\)或\(1\)
\(g(1)=1=2^n-1\)
对于第\(n\)个盘子，若在第三根柱子上\(g(n)=g(n-1)≤2^{n-1}-1\)
若不在第三根柱子上\(g(n)=g(n-1)+1+T_{n-1}≤2^n-1\)
5.不能，第四个圆与前三个圆最多有6个交点，最多增加6个表示集合
6.\(f(1)=f(2)=0,f(n)=f(n-1)+n-2=S_{n-2},n>2\)
7.\(H(1)=J(2)-J(1)=0\)
\[Q_2=\frac{1+β}{α}
\]
\[Q_3=\frac{1+\frac{1+β}{α}}{β}=\frac{1+α+β}{αβ}
\]
\[Q_4=\frac{1+\frac{1+α+β}{αβ}}{\frac{1+β}{α}}=\frac{α+\frac{1+α+β}{β}}{1+β}=\frac{1+α+\frac{1+α}{β}}{1+β}=\frac{\frac{(1+α)(1+β)}{β}}{1+β}=\frac{1+α}{β}
\]
\[Q_5=\frac{1+\frac{1+α}{β}}{\frac{1+α+β}{αβ}}=\frac{αβ+α(1+α)}{1+α+β}=\frac{α(1+α+β)}{1+α+β}=α
\]
a：
\[(\frac{x_1+…+x_n}{n})^n≥x_1…x_n
\]
\[(\frac{x_1+…+x_{n-1}+\frac{x_1+…x_{n-1}}{n-1}}{n})^n≥x_1…x_{n-1}*\frac{x_1+…+x_{n-1}}{n-1}
\]
\[(\frac{x_1+…+x_{n-1}}{n-1})^n≥x_1…x_{n-1}*\frac{x_1+…+x_{n-1}}{n-1}
\]
\[(\frac{x_1+…+x_{n-1}}{n-1})^{n-1}≥x_1…x_{n-1}
\]
b:
引理一：基本不等式：
\[ab≤(\frac{a+b}{2})^2
\]
证明：
\[(\frac{\sum_{i=1}^{n}x_i}{n})^n≥\prod_{i=1}^{n}x_i
\]
\[(\frac{\sum_{i=n+1}^{2n}x_i}{n})^n≥\prod_{i=n+1}^{2n}x_i
\]
两式相乘
\[(\frac{\sum_{i=1}^{n}x_i}{n}*\frac{\sum_{i=n+1}^{2n}x_i}{n})^n≥\prod_{i=1}^{2n}x_i
\]
由引理一得
\[(\frac{\sum_{i=1}^{2n}x_i}{2n})^{2n}≥\prod_{i=1}^{2n}x_i
\]
c.
疑问，对于a.的证明，题目给出了特定条件，是否对一般地情况成立
引用
补充对不等式的证明：
引理一：
\[x≤e^{x-1}
\]
证明：
如果存在\(x_i=0\)，那么显然成立
若任意\(x_i＞0\)，令
\[a=\frac{\sum_{i=1}^{n}x_i}{n}>0
\]
对任意\(x_i\)有
\[\frac{x_i}{a}≤e^{\frac{x_i}{a}-1}
\]
所有式子相乘得到
\[\frac{\prod_{i=1}^{n}x_i}{a^n}≤e^{\sum_{i=1}^{n}\frac{x_i}{a}-n}=e^{n-n}=1
\]
\[a^n≥\prod_{i=1}^{n}x_i
\]
\[(\frac{\sum_{i=1}^{n}x_i}{n})^n≥\prod_{i=1}^{n}x_i
\]
\(Q_n\)：先将\(n-1\)个盘子挪到\(C\)，将第\(n\)个盘子挪到\(B\)，再将\(n-1\)个盘子挪到\(B\)
\(Q_n=R_{n-1}+1+R_{n-1}=2R_{n-1}+1\)
\(R_n\)：将\(n-1\)个盘子挪到\(A\),将第\(n\)个盘子挪到\(C\),将\(n-1\)个盘子挪到\(B\),将第\(n\)个盘子挪到\(A\)，将\(n-1\)个盘子挪到\(A\)
\(R_n=R_{n-1}+1+Q_{n-1}+1+R_{n-1}=Q_n+Q_{n-1}+1\)
a.
\[P_n=2P_{n-1}+2=2^{n+1}-2
\]
b.
注意，只需要在最后恢复，经偶数次\(a\)中放置即可恢复顺序
\[Q_n=4P_{n-1}+3=4*(2^n-2)+3=2^{n+2}-5
\]
\[P_n=2P_{n-1}+m_n=\sum_{i=1}^{n}2^{n-i}m_i
\]
每条\(Z\)比三条直线少了\(5\)块区域
\[F_n=L_{3n}-5n=\frac{3n(3n+1)}{2}-5n+1=\frac{9n^2-7n+2}{2}
\]
或，第\(n\)个折线与前\(n-1\)条折线每条最多有\(9\)个交点，共计最多\(9n-9\)个交点，可新增\(9n-8\)个区域
\(F_n=F_{n-1}+9n-8=\frac{9n^2-7n+2}{2}\)$
新切一刀增加的空间数量为切面上直线划分的二维平面数量
\[P_n=P_{n-1}+L_{n-1}
\]
类似的，设\(X_n\)是一条直线上\(n\)个点所确定的一维区域的最大个数,有
\[L_n=L_{n-1}+X_{n-1}
\]
更有趣的：
\[X_n=\dbinom{n}{0}+\dbinom{n}{1}
\]
\[L_n=\dbinom{n}{0}+\dbinom{n}{1}+\dbinom{n}{2}
\]
\[P_n=\dbinom{n}{0}+\dbinom{n}{1}+\dbinom{n}{2}+\dbinom{n}{3}
\]
符合上述规律：
\[P_n=P_{n-1}+L_{n-1}=\dbinom{n-1}{0}+\dbinom{n-1}{1}+\dbinom{n-1}{2}+\dbinom{n-1}{3}+\dbinom{n-1}{0}+\dbinom{n-1}{1}+\dbinom{n-1}{2}
\]
\[=\dbinom{n-1}{0}+(\dbinom{n-1}{0}+\dbinom{n-1}{1})+(\dbinom{n-1}{1}+\dbinom{n-1}{2})+(\dbinom{n-1}{2}+\dbinom{n-1}{3})
\]
\[=\dbinom{n}{0}+\dbinom{n}{1}+\dbinom{n}{2}+\dbinom{n}{3}
\]
组合意义待探究
\(I(2)=2,I(3)=1\)
若\(n\)为偶数，第一轮删掉\(2,4,6,…\)，剩下\(1,3,5,……\),再从\(1\)开始，那么\(I(n)=2I(\frac{n}{2})-1\)
若\(n\)为奇数，第一轮过后再从\(3\)开始，那么\(I(n)=2I(\frac{n}{2})+1\)
