[NOIP2018校模拟赛]T1 阶乘

题目：###

---

描述##

有n个正整数a[i]，设它们乘积为p，你可以给p乘上一个正整数q，使p*q刚好为正整数m的阶乘，求m的最小值。

输入##

共两行。
第一行一个正整数n。
第二行n个正整数a[i]。

输出##

共一行
一个正整数m。

样例输入##

1
6

样例输出##

3

---

看到这个题目描述只有一行我心头就涌上一股不祥的预感……
一般这种题……都比较……那啥……
（是的，这个题我又写炸了……

好的让我们来分析一下这道题：

分析：###

首先我们可以知道，如果一个数的阶乘对输入的数的乘积取模等于零（实际上就是它的倍数），那么这个数m!一定是包含了输入数据相乘的所有质因子的，所以我们在读入数据的时候先把每个数都分解一下质因子，然后存储每个质因子出现的次数。

然后我们来感性理解一个奇怪的结论：
举一个例子：30!中有多少个质因子3？

首先我们把含有3的乘数提取出来，大概长这个样：
3 6 9 12 15 18 21 24 27 30
其中每个数对应含有因子3的个数为： 1 1 2 1 1 2 1 1 3 1
看出什么规律了吗？ 每两个一次项过后是一个二次项，每两个二次项过后是一个三次项，后面的规律可以以此类推。
那么这个结论是不是正确的呢？我们感性理解一下：
每一个数都除以一个3，得到的结果是： 1 2 3 4 5 6 7 8 9 10
是不是相当于降下来了一次？ 这个时候原先含有一个3的数已经不含3了，而原先含有两个3（二次项）的变成了含有一个3。
较为普适的结论要看这个图理解（我终于稍微不那么感性地搞出了这个玩意……）：

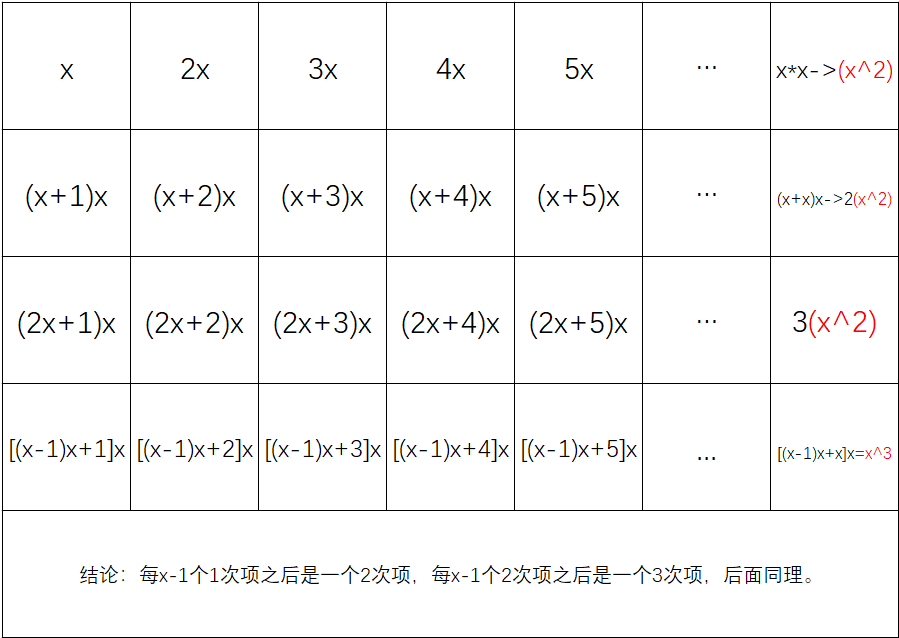
这个结论有什么用呢？事实是，用一个函数模拟上面降次的过程，就可以求出x的阶乘中含有的每个质因子的个数。

又显然，m是具有单调性的，即如果(m_i)!是符合题意的数，那么(m_j)!（其中j>i）一定也是符合题意的数（因为(m_j)!%(m_i)!==0），所以我们考虑二分一个m，然后用上面得出的结论来验证m
然后就出答案啦OvO

---

代码：###

#include<bits/stdc++.h>
using namespace std;
int prime[100005],n,max_prime=-1,x;
inline long long read(){
	long long cnt=0,f=1;char c;
	c=getchar();
	while(!isdigit(c)){if(c=='-')f=-f;c=getchar();}
	while(isdigit(c)){cnt=cnt*10+c-'0';c=getchar();}
	return cnt*f;
}
bool check(int x){
	if(x<max_prime)return false;  //如果x已经小于了最大的质因子max_prime，那么x!中一定不含有 max_prime这个质因子，直接return false 
	for(register int i=2;i<=max_prime;i++){
		if(!prime[i])continue;
		int xx=x,t=0;
		while(xx){
			t+=xx/i;
			xx/=i;
		}
		if(t<prime[i])return false;  //如果发现这个数的阶乘中某一个质因子的次数小于输入中的质因子的次数则非法 
	}
	return true; 
}
int main(){
	n=read();
	for(register int i=1;i<=n;i++){
		x=read();
		for(register int j=2;j<=sqrt(x);j++)
			while(x%j==0)x/=j,prime[j]++,max_prime=max(max_prime,j);
		if(x>1)prime[x]++,max_prime=max(max_prime,x);
	}
	int l=1,r=1e9;
	while(l<r){
		int mid=(l+r)>>1;
		if(check(mid))r=mid;
		else l=mid+1;
	}
	printf("%d",l); 
	return 0;
}