浅谈关于树形dp求树的直径问题

在一个有n个节点，n-1条无向边的无向图中，求图中最远两个节点的距离，那么将这个图看做一棵无根树，要求的即是树的直径。####

求树的直径主要有两种方法：树形dp和两次bfs/dfs，因为我太菜了不会写后者这里只介绍树形dp

• 树形dp求树的直径
  我们不妨设1号点为根节点，那么这就可以看做一棵有根树。
  设D[x]表示从节点x出发，往以x为根的子树走，能够到达的最远距离。设x的子节点分别为\(y_1,y_2,y_3,...,y_t\)，\(edge(x,y)\)表示从x到y的边权，则可以得到状态转移方程：
  \(D[x]={(D[y_i]+edge(x,y_i))}_{max}\)
  接下来，我们考虑对于每个节点x求出经过x的最长链的长度F[x],整棵树的直径就是max{F[x]}(1<=x<=n)。

  现在我们考虑如何求F[x]。
  对于任意两个节点yi和yj，经过节点x的最长链的长度可以通过四个部分来构成：

  • D[yi]
  • D[yj]
  • 从x到yi的距离
  • 从x到yj的距离

  不妨设j<i，则有：

\(F[x]= {(D[y_i]+D[y_j]+edge(x,y_i)+edge(x,y_j))}_{max}\)

对应代码如下：

void dp(int x){
	v[x]=1;	
	for(register int i=head[x];i;i=nxt[i]){
		int y=ver[i];
		if(v[y])continue;	
		dp(y); 
		ans=max(ans,d[x]+d[y]+edge[i]);
		d[x]=max(d[x],d[y]+edge[i]);
	}
}

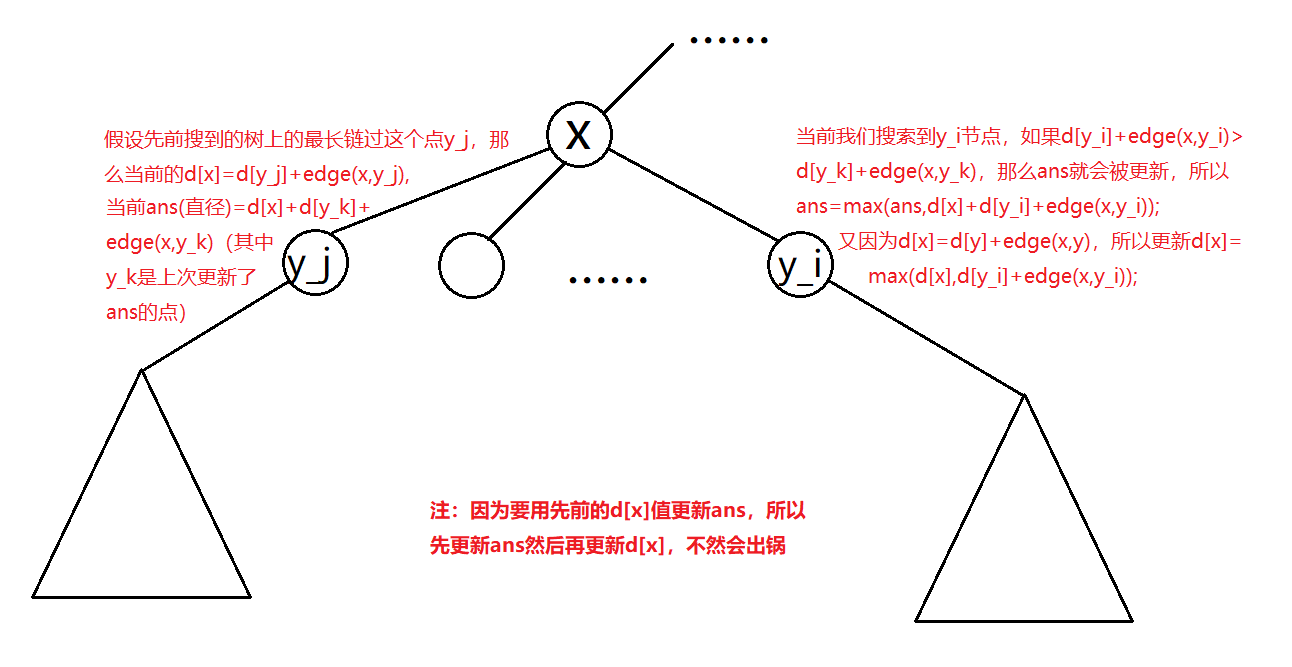
代码解释可以看图：

参考资料：李煜东《算法竞赛进阶指南》