Codeforces Round #428 (Div. 2)A,B,C

A. Arya and Bran

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Bran and his older sister Arya are from the same house. Bran like candies so much, so Arya is going to give him some Candies.

At first, Arya and Bran have 0 Candies. There are n days, at the i-th day, Arya finds ai candies in a box, that is given by the Many-Faced God. Every day she can give Bran at most 8 of her candies. If she don't give him the candies at the same day, they are saved for her and she can give them to him later.

Your task is to find the minimum number of days Arya needs to give Bran k candies before the end of the n-th day. Formally, you need to output the minimum day index to the end of which k candies will be given out (the days are indexed from 1 to n).

Print -1 if she can't give him k candies during n given days.

Input

The first line contains two integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 10000).

The second line contains n integers a1, a2, a3, ..., an (1 ≤ ai ≤ 100).

Output

If it is impossible for Arya to give Bran k candies within n days, print -1.

Otherwise print a single integer — the minimum number of days Arya needs to give Bran k candies before the end of the n-th day.

Examples

input

2 3
1 2

output

2

input

3 17
10 10 10

output

3

input

1 9
10

output

-1

Note

In the first sample, Arya can give Bran 3 candies in 2 days.

In the second sample, Arya can give Bran 17 candies in 3 days, because she can give him at most 8 candies per day.

In the third sample, Arya can't give Bran 9 candies, because she can give him at most 8 candies per day and she must give him the candies within 1 day.

 

 

思路：水题

代码：

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<set>
#include<list>
using namespace std;
#define ll long long
#define sd(x) scanf("%d",&x)
#define sdd(x,y) scanf("%d%d",&x,&y)
#define sddd(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define sf(x) scanf("%s",x)
#define ff(i,x,y) for(int i = x;i <= y;i ++)
#define fj(i,x,y) for(int i = x;i >= y;i --)
#define mem(s,x) memset(s,x,sizeof(s));
#define pr(x) printf("%d",x);
const int Mod = 1e9+7;
const int inf = 1e9;
const int Max = 1e4+10;
//void exgcd(ll a,ll b,ll& d,ll& x,ll& y){if(!b){d=a;x=1;y=0;}else{exgcd(b,a%b,d,y,x);y-=x*(a/b);}}
//ll inv(ll a,ll n){ll d, x, y;exgcd(a,n,d,x,y);return (x+n)%n;}  ��Ԫ
//int gcd(int a,int b)  {  return (b>0)?gcd(b,a%b):a;  }  ��С��Լ
//int lcm(int a, int b)  {  return a*b/gcd(a, b);   }    ������
int main()
{
    int i,ans=0,sum=0,a[Max],n,k;
    cin>>n>>k;
    for(i=0;i<n;i++){
        cin>>a[i];
        if(a[i]>=8){
            ans+=a[i]-8;
            a[i] = 8;
        }
        else{
            if(ans>0&&ans+a[i]>8){
                ans -= (8-a[i]);
                a[i] = 8;
            }
            else if(ans>0&&ans+a[i]<=8){
                //cout<<a[i]<<endl;
                a[i] += ans;
                ans = 0;
                //cout<<a[i]<<endl;
            }
        }
        //cout<<ans<<endl;
    }
    for(i=0;i<n;i++){
        sum += a[i];
        if(sum>=k){
            cout<<i+1<<endl;
            return 0;
        }
    }
    cout<<"-1"<<endl;
    return 0;

B. Game of the Rows

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Daenerys Targaryen has an army consisting of k groups of soldiers, the i-th group contains ai soldiers. She wants to bring her army to the other side of the sea to get the Iron Throne. She has recently bought an airplane to carry her army through the sea. The airplane has nrows, each of them has 8 seats. We call two seats neighbor, if they are in the same row and in seats {1, 2}, {3, 4}, {4, 5}, {5, 6} or {7, 8}.

A row in the airplane

Daenerys Targaryen wants to place her army in the plane so that there are no two soldiers from different groups sitting on neighboring seats.

Your task is to determine if there is a possible arranging of her army in the airplane such that the condition above is satisfied.

Input

The first line contains two integers n and k (1 ≤ n ≤ 10000, 1 ≤ k ≤ 100) — the number of rows and the number of groups of soldiers, respectively.

The second line contains k integers a1, a2, a3, ..., ak (1 ≤ ai ≤ 10000), where ai denotes the number of soldiers in the i-th group.

It is guaranteed that a1 + a2 + ... + ak ≤ 8·n.

Output

If we can place the soldiers in the airplane print "YES" (without quotes). Otherwise print "NO" (without quotes).

You can choose the case (lower or upper) for each letter arbitrary.

Examples

input

2 2
5 8

output

YES

input

1 2
7 1

output

NO

input

1 2
4 4

output

YES

input

1 4
2 2 1 2

output

YES

Note

In the first sample, Daenerys can place the soldiers like in the figure below:

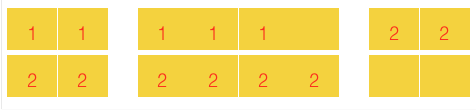
In the second sample, there is no way to place the soldiers in the plane since the second group soldier will always have a seat neighboring to someone from the first group.

In the third example Daenerys can place the first group on seats (1, 2, 7, 8), and the second group an all the remaining seats.

In the fourth example she can place the first two groups on seats (1, 2) and (7, 8), the third group on seats (3), and the fourth group on seats (5, 6).

 

 思路：主要坑点为四座的处理上，首先优先排四座，剩余的去二座，那么剩下的四座若要最大利用，设分三组：

1 1 * 2

3 3 *2

*表示不坐人，四座可分为两座和一座，加到两座里继续去排，两座排完，还有剩余两座位置加上剩余四座当成一座去排。

实现代码：

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<set>
#include<list>
using namespace std;
#define ll long long
#define sd(x) scanf("%d",&x)
#define sdd(x,y) scanf("%d%d",&x,&y)
#define sddd(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define sf(x) scanf("%s",x)
#define ff(i,x,y) for(int i = x;i <= y;i ++)
#define fj(i,x,y) for(int i = x;i >= y;i --)
#define mem(s,x) memset(s,x,sizeof(s));
#define pr(x) printf("%d",x);
#define pb(x) push_back(x);
const int Mod = 1e9+7;
const int inf = 1e9;
const int Max = 1e5+10;
vector<int>vt[Max];
//void exgcd(ll a,ll b,ll& d,ll& x,ll& y){if(!b){d=a;x=1;y=0;}else{exgcd(b,a%b,d,y,x);y-=x*(a/b);}}
//ll inv(ll a,ll n){ll d, x, y;exgcd(a,n,d,x,y);return (x+n)%n;}  ��Ԫ
//int gcd(int a,int b)  {  return (b>0)?gcd(b,a%b):a;  }  ��С��Լ
//int lcm(int a, int b)  {  return a*b/gcd(a, b);   }    ������
int main()
{
    int n,k,a[109],i;
    cin>>n>>k;
    for(i=0;i<k;i++){
        cin>>a[i];
    }
    int cnt1 = n,cnt;
    for(i=0;i<k;i++){
        cnt = min(a[i]/4,cnt1);
        cnt1 -= cnt;
        a[i] -= cnt*4;
    }
    int cnt2 = n*2+cnt1;
    for(i=0;i<k;i++){
        cnt = min(a[i]/2,cnt2);
        cnt2 -= cnt;
        a[i] -= cnt*2;
    }
    int cnt3 = cnt1+cnt2;
    for(i=0;i<k;i++){
        cnt3-=a[i];
    }
    if(cnt3>=0)
        cout<<"YES"<<endl;
    else
        cout<<"NO"<<endl;
    return 0;
}

C. Journey

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

There are n cities and n - 1 roads in the Seven Kingdoms, each road connects two cities and we can reach any city from any other by the roads.

Theon and Yara Greyjoy are on a horse in the first city, they are starting traveling through the roads. But the weather is foggy, so they can’t see where the horse brings them. When the horse reaches a city (including the first one), it goes to one of the cities connected to the current city. But it is a strange horse, it only goes to cities in which they weren't before. In each such city, the horse goes with equal probabilities and it stops when there are no such cities.

Let the length of each road be 1. The journey starts in the city 1. What is the expected length (expected value of length) of their journey? You can read about expected (average) value by the link https://en.wikipedia.org/wiki/Expected_value.

Input

The first line contains a single integer n (1 ≤ n ≤ 100000) — number of cities.

Then n - 1 lines follow. The i-th line of these lines contains two integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — the cities connected by the i-th road.

It is guaranteed that one can reach any city from any other by the roads.

Output

Print a number — the expected length of their journey. The journey starts in the city 1.

Your answer will be considered correct if its absolute or relative error does not exceed 10 - 6.

Namely: let's assume that your answer is a, and the answer of the jury is b. The checker program will consider your answer correct, if .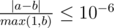

Examples

input

4
1 2
1 3
2 4

output

1.500000000000000

input

5
1 2
1 3
3 4
2 5

output

2.000000000000000

Note

In the first sample, their journey may end in cities 3 or 4 with equal probability. The distance to city 3 is 1 and to city 4 is 2, so the expected length is 1.5.

In the second sample, their journey may end in city 4 or 5. The distance to the both cities is 2, so the expected length is 2.

思路：基础dfs。

实现代码：

#include<bits/stdc++.h>
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<map>
#include<queue>
#include<stack>
#include<set>
#include<list>
using namespace std;
#define ll long long
#define sd(x) scanf("%d",&x)
#define sdd(x,y) scanf("%d%d",&x,&y)
#define sddd(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define sf(x) scanf("%s",x)
#define ff(i,x,y) for(int i = x;i <= y;i ++)
#define fj(i,x,y) for(int i = x;i >= y;i --)
#define mem(s,x) memset(s,x,sizeof(s));
#define pr(x) printf("%d",x);
#define pb(x) push_back(x);
const int Mod = 1e9+7;
const int inf = 1e9;
const int Max = 1e5+10;
vector<int>vt[Max];
//void exgcd(ll a,ll b,ll& d,ll& x,ll& y){if(!b){d=a;x=1;y=0;}else{exgcd(b,a%b,d,y,x);y-=x*(a/b);}}
//ll inv(ll a,ll n){ll d, x, y;exgcd(a,n,d,x,y);return (x+n)%n;}  ��Ԫ
//int gcd(int a,int b)  {  return (b>0)?gcd(b,a%b):a;  }  ��С��Լ
//int lcm(int a, int b)  {  return a*b/gcd(a, b);   }    ������
double dfs(int u,int fa,int dep){
    double ans=0;
    int cnt = 0;
   for(int i=0;i<(int)vt[u].size();i++){
      int v = vt[u][i];
      if(v!=fa){
        cnt++;
        ans+=dfs(v,u,dep+1);
      }
   }
   ans = cnt ? ans / (1.0 * cnt) : 1.0 * dep;
   return ans;
}
int main()
{
    int n,i,u,v;
    cin>>n;
    for(i=0;i<n-1;i++){
        cin>>u>>v;
        vt[u].pb(v);
        vt[v].pb(u);
    }
    printf("%.8lf\n",dfs(1,-1,0));
}