格子方法曲边处理

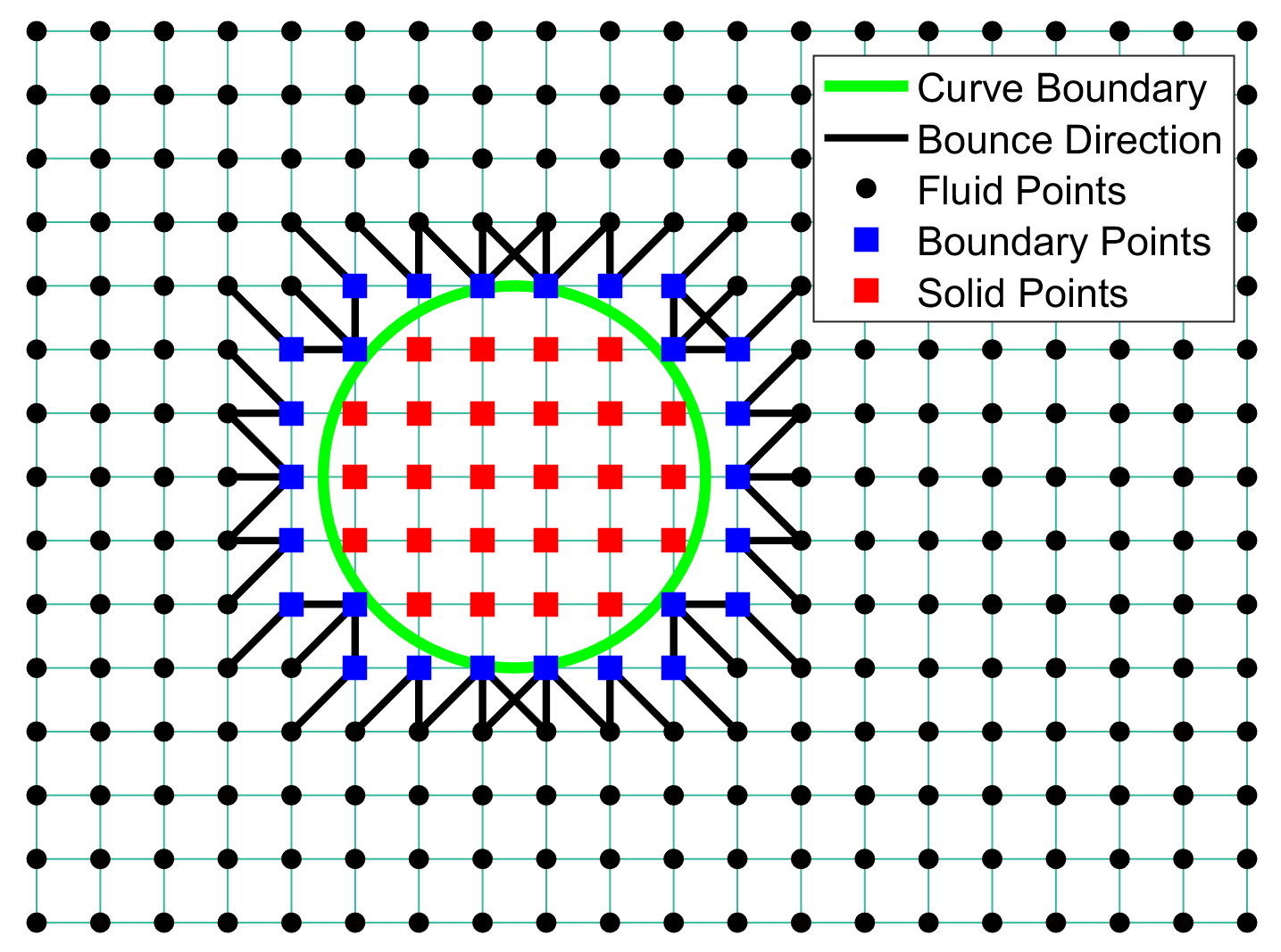
　　应用格子玻尔兹曼方法做气固两相流时，对于颗粒相，借助相关作用力模型，可视为点源处理，也可以直接解析颗粒，精确刻画颗粒气体间相互作用力。全解析颗粒时，一般可将颗粒视为球体（三维）或者圆（二维），气体颗粒间相互作用体现在颗粒边界的的处理上，对于这样的曲边界，其处理方法的好坏直接影响计算的精度和稳定性，对于无滑移的曲边界，有将曲边近似为阶梯状的直接反弹法、在其基础上改进的插值反弹法，及基于构造虚拟固体点上分布函数的F-H、MLS、GZS方法等。上述方法中除直接反弹法外，其他几种方法无一例外的都需要求解曲边同其穿过的格点连线的交点及其交点在线段上的位置百分比，对于曲边附近的边界点，需要频繁求解该位置百分比及交点，故将此写成一个小函数，方便主函数调用。

　　给出的代码中将曲边视为一个圆，可以通过圆心、半径来刻画，而格点连线可以通过连线两端点来描述，圆和直线都可以用解析式来表征，只需要联立圆和直线方程即可求解该交点及其百分比。

 

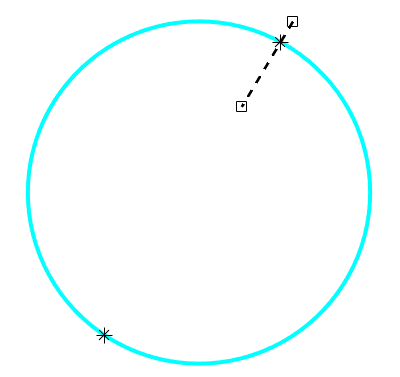
/// To compute the q for interpolated bounce back
/// Parameter cir_x, cir_y, cir_r: center point location and radius of the particle, is the curve boundary
/// Parameter bpx, bpy: the location of the end point outside the circle, is the boundary point
/// Parameter spx, spy: the location of the end point inside the circle, is the solid point
double cal_q ( double cir_x, double cir_y, double cir_r, double bpx, double bpy, double spx, double spy ) {
    double k, b, A, B, C, x1, x2, y1, y2, q1, q2, q;
    if ( bpx != spx ) {  // ensure that k is exists
        // line parameter
        k = ( spy - bpy ) / ( spx - bpx );
        b = spy - k * spx;
        // equation parameter
        A = k * k + 1;
        B = 2 * k * ( b - cir_y ) - 2 * cir_x;
        C = ( b - cir_y ) * ( b - cir_y ) + cir_x * cir_x - cir_r * cir_r;
        // solve the equation
        x1 = ( -B + sqrt ( B * B - 4 * A * C ) ) / 2 / A;
        x2 = ( -B - sqrt ( B * B - 4 * A * C ) ) / 2 / A;
        q1 = ( bpx - x1 ) / ( bpx - spx );
        q2 = ( bpx - x2 ) / ( bpx - spx );
    } else {  // x1 = x2 = bpx = spx
        y1 = cir_y + sqrt ( cir_r * cir_r - ( bpx - cir_x ) * ( bpx - cir_x ) );
        y2 = cir_y - sqrt ( cir_r * cir_r - ( bpx - cir_x ) * ( bpx - cir_x ) );
        q1 = ( bpy - y1 ) / ( bpy - spy );
        q2 = ( bpy - y2 ) / ( bpy - spy );
    }
    // determine the final result
    if ( q1 >= 0 && q1 <= 1 ) {
        q = q1;
    } else {
        q = q2;
    }
    return q;
33 }