AutoEncoder详解

前言

AutoEncoder是深度学习的另外一个重要内容，并且非常有意思，神经网络通过大量数据集，进行end-to-end的训练，不断提高其准确率，而AutoEncoder通过设计encode和decode过程使输入和输出越来越接近，是一种无监督学习过程。

AutoEncoder

Introduction

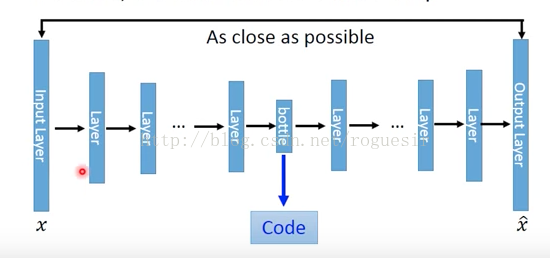
AutoEncoder包括两个过程：encode和decode，输入图片通过encode进行处理，得到code，再经过decode处理得到输出，有趣的是，我们控制encode的输出维数，就相当于强迫encode过程以低维参数学习高维特征，这导致的结果和PCA类似。

AutoEncoder的目的是使下图中的输入x和输出x_head越相似越好，这就需要在每次输出之后，进行误差反向传播，不断优化。

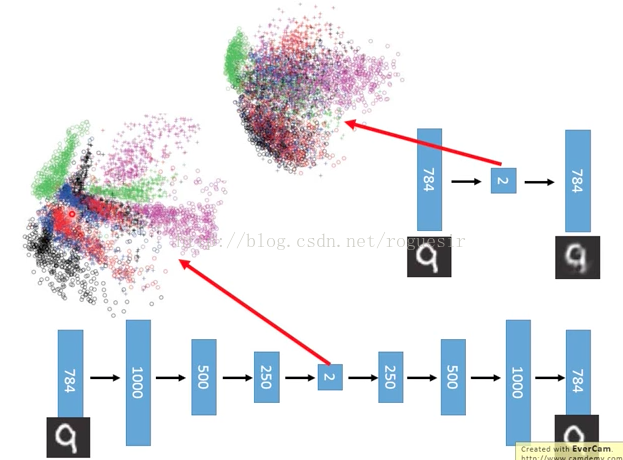
高维数据对于我们的感官体验总是不友好，如果我们将输入降低至二维，放在二维平面中就会更加直观，下图是MNIST数据集做AutoEncoder：

上面是PCA的结果，下面是AutoEncoder的结果，在二维中结果很清晰。

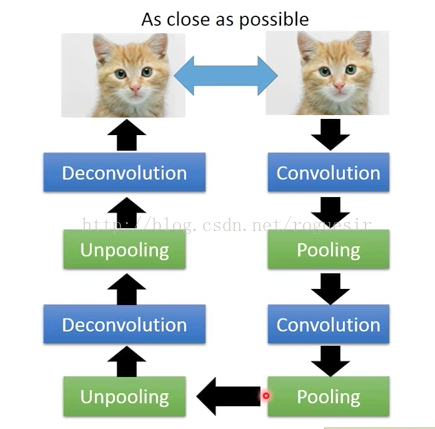
encode和decode两个过程可以理解成互为反函数，在encode过程不断降维，在decode过程提高维度。当AutoEncoder过程中用卷积操作提取特征，相当于encode过程为一个深度卷积神经网络，好多层的卷积池化，那么decode过程就需要进行反卷积和反池化，那么，反卷积和反池化如何定义呢？

Unpooling

池化过程实际上就是降维过程，假设图片大小为32x32，池化大小为2x2，就相当于将图片中相邻的2x2个像素点替换为四个点中最大数值（max-pooling），池化处理之后得到的图片大小为16x16，Unpooling过程则需要将16x16的图片变为32x32，其实在池化过程中，会标记2x2像素点中最大值的位置，在Unpooling过程将最大值还原，其他位置填0。

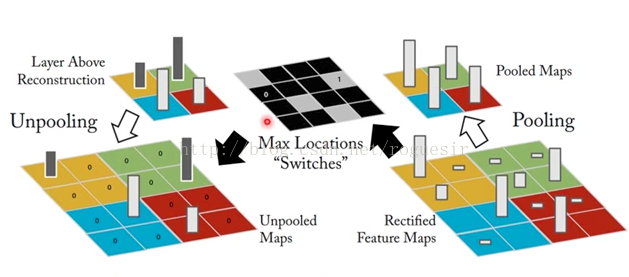
以上并不是Unpooling的唯一做法，在Keras中，不会记住最大值的位置，而是将所有像素均以最大值填充。

Deconvolution

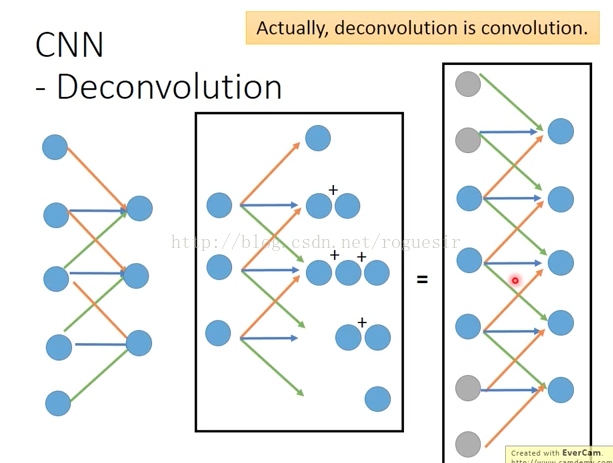
卷积过程是一个矩阵在另一个矩阵上面做滑动运算，反卷积也是一样，实际上，反卷积就是卷积，看下面的图，我们熟悉的是左面的卷积过程，假设有5个像素点，卷积核为3，步长为1，卷积之后生成3个feature，我们想象中的反卷积应该是中间所示的情形，由3个输入生成5个输出，如果我们将反卷积中的输入做2的padding，这样原本3个输入变成7个输入，再做卷积，生成5个输出，对比左右两侧的图，是完全相反的，所以，我们加上padding，使反卷积变成了卷积运算。

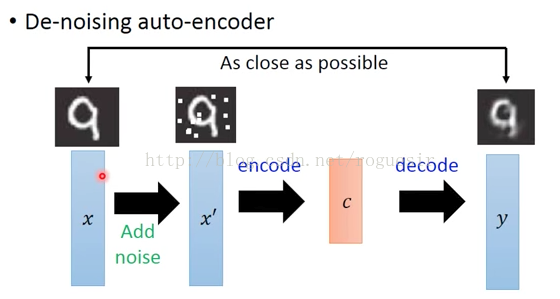
De-noising AutoEncoder

对于AutoEncoder，每一次的训练都是自身的对比，这回造成输出和输入越来越类似，而对同种类的其他图片表现不敏感，于是，De-noising AutoEncoder派上了用场，如下图所示，在输入之前，先将图片加入随机噪声，这样每次的输入都会略有差异，然后将带有噪声的图片进行AutoEncoder，将输出的y与加噪声之前的图片进行比较，这样训练出来的y就具有抗噪声的能力，在以图搜图的场景下也就提高了泛化能力。