机器学习python实战----逻辑回归

　　当看到这部分内容的时候我是激动的，因为它终于能跟我之前学习的理论内容联系起来了，这部分内容就是对之前逻辑回归理论部分的代码实现，所以如果有不甚理解的内容可以返回对照着理论部分来理解，下面我们进入主题----logistic regression

一、sigmoid函数

　　在之前的理论部分我们知道，如果我们需要对某物进行二分类，那么我们希望输出函数的值在区间[0,1]，于是我们引入了sigmoid函数。函数的形式为。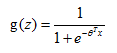

曲线图

　　

根据函数表达式，我们可以用代码来表示

def sigmoid(Inx):
    return 1.0/(1+exp(-Inx))

二、梯度上升法

　　这里采用的方法为梯度上升法。其实梯度上升法跟梯度下降法的原理是一样的，不过是换种形式表达。梯度上升法的公式表示为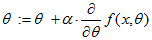，梯度下降法的公式表示为。这里虽然看上去只有一个运算符不同，事实上这里的f(x,θ)也是有些小区别，在后面的代码中我会解释一下。

　　这里首先还是要从文本文件中获取特征数据集和标签，方法在之前已经阐述过几次了，这部分就直接给出代码。得到了特征数据集和标签，我们就可以用梯度上升法和梯度下降法来寻找最佳参数

def loaddataSet(filename):
    dataMat = []
    labelsVec = []
    file = open(r'logRegres\testSet.txt')
    for line in file.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelsVec.append(int(lineArr[-1]))
    return dataMat,labelsVec

def GradAscent(dataSetIn,classLabels):  #梯度上升法
    dataMat = mat(dataSetIn)
    labelsVec = mat(classLabels).transpose()
    m,n = shape(dataMat)
    sigma = ones((n,1))
    alpha = 0.001
    maxCycles = 500
    for i in range(maxCycles):
        h = sigmoid(dataMat*sigma)
        error = (labelsVec-h)
        sigma = sigma + alpha*dataMat.transpose()*error
    return sigma

def GradAscent1(dataSetIn,classLabels):   #梯度下降法
    dataMat = mat(dataSetIn)
    labelsVec = mat(classLabels).transpose()
    m,n = shape(dataMat)
    sigma = zeros((n,1))
    alpha = 0.001
    maxCycles = 500
    for i in range(maxCycles):
        h = sigmoid(dataMat*sigma)
        error = (h-labelsVec)
        sigma = sigma - alpha*dataMat.transpose()*error
    return sigma

这里的.transpose()方法是对矩阵进行转置，maxCycles为迭代次数。上面说的梯度下降法与梯度上升法的f(x,θ)的区别在误差error，两种方法的error互为相反数。其实只要把梯度下降法的error代入sigma = sigma - alpha*dataMat.transpose()*error就可以发现，将error的负号提出来得到的就跟梯度上升法一样的式子了。这里的参数sigma的更新我们省略了推导过程，不熟悉的可以去之前理论部分看看。得到了最佳参数之后，我们就可以画出决策边界来看看是否能完美的契合数据集。

def plotBestFit(sigma): #sigma为numpy数组的形式传入
    dataMat,labelsVec = loaddataSet(r'logRegres\testSet.txt')
    ArrdataMat = array(dataMat)
    n = shape(ArrdataMat)[0]
    #sigmaT = GradAscent(dataMat,labelsVec)
    #sigma = sigmaT.getA()
    xcord1=[];ycord1=[]
    xcord2=[];ycord2=[]
    for i in range(n):
        if labelsVec[i]==1:
            xcord1.append(ArrdataMat[i,1])
            ycord1.append(ArrdataMat[i,2])
        else:
            xcord2.append(ArrdataMat[i,1])
            ycord2.append(ArrdataMat[i,2])
    fig = plt.figure()
    ax = plt.subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c = 'red',marker = 's')
    ax.scatter(xcord2,ycord2,s=30,c = 'blue')
    x = arange(-3.0,3.0,0.1)
    y=(-sigma[0]-sigma[1]*x)/sigma[2]
    ax.plot(x,y)
    plt.show()

这个函数中调用了之前的loaddataSet()函数，这里需要修改为自己电脑上文本文件所在路径。然后我们把数据集中的两个类别0、1分开显示以便看得更清晰，之后就是绘制决策边界了。y=(-sigma[0]-sigma[1]*x)/sigma[2]这个表达式是怎么来的呢？我们的特征向量X = [x0,x1,x2]，x0=1，表达式中的x相当于x1，y相当于x2，因此我们就用这个式子来表示决策边界。结果显示如下

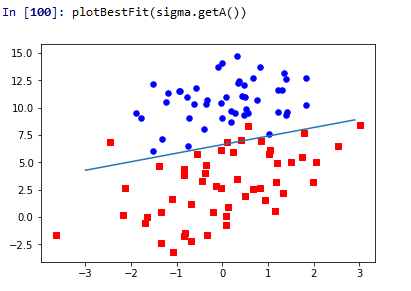
这里只给出了梯度上升法的结果图，梯度下降法得到的结果跟这个一模一样，有兴趣的可以自己绘制出来试试。图中可以看出分类的效果还是蛮不错的。但是，这种方法存在一个问题，就是计算复杂度较高，对于数百个样本可以，但是如果有数百万的样本呢？下面我们会对上面的算法进行优化。

三、随机梯度上升法

　　随机梯度上升法的原理是：一次只用一个样本点来更新回归系数。代码如下

def stocGradAscent0(dataMat,labelsVec):
    ArrdataMat = array(dataMat)
    m,n = shape(ArrdataMat)
    sigma = ones(n)
    alpha = 0.01
    for i in range(m):
        h = sigmoid(sum(ArrdataMat[i]*sigma))
        error = float(labelsVec[i] - h)
        sigma = sigma+alpha*error*ArrdataMat[i]
    return sigma
    

我们可以看出，代入sigmoid函数的不再是整个特征数据集，而只是一个样本点，这样计算量就比之前的方法小了很多了。我们来看下这样做的效果

红色部分有将近一半的数据划分产生的错误。那这种方法是不是不好呢？当然不是，这里我们只运算了一次，还没有开始迭代，而优化之前的方法我们迭代了500次，所以这并不能看出来优化后的方法的效果。下面我们会修改代码，进行150次迭代再来看看效果

def stocGradAscent1(dataMat,labelsVec,numIter = 150):
    ArrdataMat = array(dataMat)
    m,n = shape(ArrdataMat)
    sigma = ones(n)
    for i in range(numIter):
        for j in range(m):
            alpha = 1.0/(1+i+j)+0.01
            randIndex = int(random.uniform(0,m))
            h = sigmoid(sum(ArrdataMat[randIndex]*sigma))
            error = labelsVec[randIndex]-h
            sigma = sigma+alpha*error*ArrdataMat[randIndex]
    return sigma

这里的第三个默认参数numIter是迭代次数，默认是150，我们可以自己指定。代码中的alpha是变化的，会随着迭代次数不断减少，但不会减到0，因为有一个常数项，这样做是为了保证在多次迭代后对新数据仍有一定的影响。这里的样本点也需要计算机随机选择，以减少周期性的波动。我们来看下结果吧

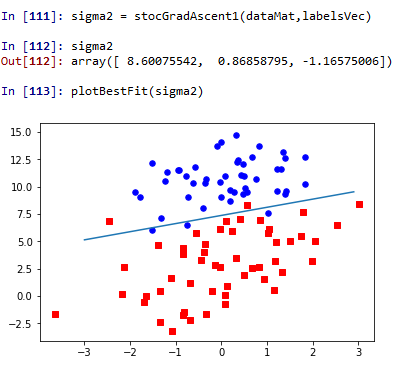
跟优化前的结果进行比较，效果还是不错的，但是这里的计算复杂度就小了很多很多了。

四、实战演练

　　这里给出一些文本文件数据集，有30%的数据缺失。经过数据的预处理，特征的缺失我们用实数0来代替，而标签的缺失我们选择丢弃该条数据。我们需要从训练集数据中提取特征数据集和标签对模型进行训练，然后用测试数据集测试训练效果。当然给出的这里的测试我们用测试数据特征集与训练模型找到的最佳回归系数相乘并代入sigmoid函数，我们之前的理论中说过，只要sigmoid函数值大于0.5，我们可以认为其分类是1，否则认为分类为0.

 

def classifyVector(Inx,sigma):
    prob = sigmoid(sum(Inx*sigma))
    if prob>0.5:
        return 1.0
    else:
        return 0.0
    
def colicTest():
    Trainfile = open(r'D:\ipython\logRegres\horseColicTraining.txt')
    Testfile = open(r'D:\ipython\logRegres\horseColicTest.txt')
    TrainSet = [];TrainLabels = []
    for line in Trainfile.readlines():
        line_s = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(line_s[i]))
        TrainSet.append(lineArr)
        TrainLabels.append(float(line_s[-1]))
    sigma = stocGradAscent1(TrainSet,TrainLabels,500)
    error_cnt=0.0;numTestVec = 0
    for line1 in Testfile.readlines():
        numTestVec+=1
        line_s1 = line1.strip().split('\t')
        lineArr1 = []
        for j in range(21):
           lineArr1.append(float(line_s1[j]))
        if int(classifyVector(array(lineArr1),sigma))!=int(line_s1[-1]):
            error_cnt+=1
    error_rate = float(error_cnt)/numTestVec
    print('the num of error is %d,the error rate is %f\n '%(error_cnt,error_rate))
    return error_rate
    
def multiTest():
    numTests = 10
    error_sum = 0.0
    for i in range(numTests):
        error_sum+=colicTest()
    print('%d iterations the average error rate is %f\n'%(numTests,float(error_sum)/numTests))

最后一个函数是进行10次测试并取平均值。这里一定要注意的一个问题是：利用.split()方法分隔得到的是str，也就是说是'2.0','1.0'的形式，这并不是数字，当然在测试时预测的分类(数字)跟标签中(str)也就是不相等的。所以这里一定要注意，如果你也产生的error_rate=1的结果，可以查看是不是犯了跟我一样的错误！

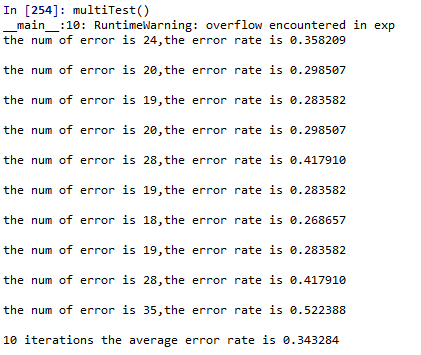
这里的预测结果中有34.3%的错误率，这个结果其实并不差，因为我们使用的数据集中有30%的数据缺失。

 

数据集及代码下载 http://pan.baidu.com/s/1qYHT3i8