MATLAB数字图像处理（二）图像增强

1 图像增强

1.1 直方图均衡化

对于灰度图像，可以使用直方图均衡化的方法使得原图像的灰度直方图修正为均匀的直方图。

代码如下：

I2=histeq(I1);
figure,imshow(I2);
figure,imhist(I2);

原图像为lena的图片，经过直方图均衡化后的图片为Figure 1。

Figure 1

原图灰度直方图请参见：MATLAB数字图像处理（一）基础操作和傅立叶变换，经过修正后的灰度直方图为Figure 2：

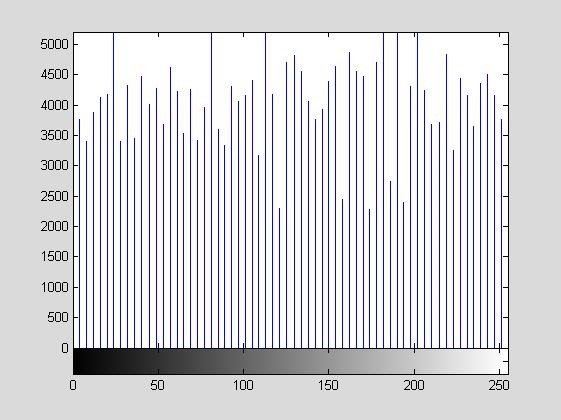
Figure 2

可以看出，与原图对比，灰度分布更加均匀。

1.2 灰度变换

在MATLAB中，可以使用imadjust函数对图像进行线性变换。常用的为线性变换。使用的函数为imadjust(I, [low_in, high_in], [low_out high_out],gamma)，其中，in为输入的图片变化的灰度范围，out为输出的图片变化的灰度范围，均为[0 1]之间。也就是将low_in和high_in之间的值映射到low_out和high_out之间。gamma为线性值，若为1则为线性变换。

代码和效果如下：

I3=imadjust(I1,[0.3 0.7],[0.1 0.9],1);
figure,imshow(I3);
figure,imhist(I3);

Figure 3

Figure 4

其中，突出了原图0.3-0.7之间的灰度元素。

1.3 空间域平滑

图像平滑是为了抑制图像噪声，改善图像质量而进行的图片处理。在这里，笔者将首先介绍MATLAB中自带的均值滤波和中值滤波实现，之后设计自己的模版算子，再次分别实现了均值滤波和中值滤波。

MATLAB中自带的均值滤波可以采用fspecial(‘params’,n)函数实现，其中，params代表的是滤波的种类，常用的有average（均值滤波），还有可以在空间域锐化中用到的高斯、拉普拉斯、prewitt、sobel算子等。n代表的是模版的在这里仅仅介绍均值滤波。

MATLAB中，均值滤波代码如下：

avgModel=fspecial('average',3);
Iavg=filter2(avgModel,I2)/255;
figure,imshow(Iavg);

由于均值滤波对于高斯噪声效果较好，故对高斯噪声的图（参见MATLAB数字图像处理（一）基础操作和傅立叶变换）进行了图像平滑。效果如下（Figure 5）：

Figure 5

而笔者根据均值滤波原理，自己写了一段代码，如下：

n=3;
model(1:n,1:n)=1;
Iavg=I2;
for i=2:length(Iavg)-1
    for j=2:length(Iavg(2,:))-1
        x=I2(i-(n-1)/2:i+(n-1)/2,j-(n-1)/2:j+(n-1)/2);
        xuint=uint8(model).*uint8(x);
        x_avg=mean(xuint(:));
        Iavg(i,j)=x_avg;
    end
end
figure,imshow(Iavg);

效果（Figure 6）：

Figure 6

可以发现，除了运行速度稍慢，效果与MATLAB自带的函数相同。

MATLAB中自带的中值滤波可以采用medfilt2(I,[n n])函数实现，其中，I代表的是需要处理的图片，n代表的是模版的大小。

MATLAB中，中值滤波代码如下：

Imid=medfilt2(I3,[3,3]);
figure,imshow(Imid);

由于中值滤波对于椒盐噪声效果较好，故对椒盐噪声的图（参见MATLAB数字图像处理（一）基础操作和傅立叶变换）进行了图像平滑。效果如下（Figure 7）：

Figure 7

而笔者根据中值滤波原理，自己写了一段代码，如下：

n=3;
Imid=I3;
for i=2:length(I1)-1
    for j=2:length(I1(2,:))-1
        x=I3(i-(n-1)/2:i+(n-1)/2,j-(n-1)/2:j+(n-1)/2);%3*3
        x_mid=median(x(:));
        Imid(i,j)=x_mid;
    end
end
figure,imshow(Imid);

效果（Figure 8）：

Figure 8

可以发现，除了运行速度稍慢，效果与MATLAB自带的函数相同。

1.4 空间域锐化

图像锐化有多种方法，最常用的锐化算子包括梯度算子、Roberts算子、Prewitt算子、Sobel算子以计算梯度的梯度锐化法，Laplacian算子等。接下来，笔者将一一介绍相关的算子。

笔者根据梯度算子的计算原理，编写了如下代码：

Igrad=I1;
for i=1:length(Igrad)-1
    for j=1:length(Igrad(2,:))-1
        x=I1(i,j+1)-I1(i,j);
        y=I1(i+1,j)-I1(i,j);
        grad=max(abs(x),abs(y));
        Igrad(i,j)=grad;%¸³Öµ
    end
end
figure,imshow(Igrad);

效果（Figure 9）：

Figure 9

MATLAB中自带了Prewitt算子和Sobel算子的函数，代码及效果如下：

model=fspecial('prewitt');
Iprewitt=filter2(model,I1);
figure,imshow(Iprewitt);

Figure 10

model=fspecial('sobel');
Isobel=filter2(model,I1);
figure,imshow(Isobel);

Figure 11

事实上，可以发现这几种算子之间不同的地方只是在于模版，因此笔者编写了一个可以自定义各种模版的代码，如下：

n=2
modelx=[-1 0;0 1];
modely=[0 -1;1 0];
Iend=I1;
Idouble=double(I1);
for i=1:length(Idouble)-5+n
    for j=1:length(Idouble(2,:))-5+n
        area=Idouble(i:i+n-1,j:j+n-1);
        x=area.*modelx;
        y=area.*modely;
        grad=max(abs(sum(x(:))),abs((sum(y(:)))));
        Iend(i,j)=grad;%¸³Öµ
    end
end
figure,imshow(Iend);

可以显示出Roberts算子的效果：

Figure 12

与Prewitt算子、Sobel算子经过对比后发现效果相同，说明有效。

对于Laplacian算子，同样可以使用MATLAB中自带的函数，也可以进行自定义。自带函数使用方法如下：

model=fspecial('laplacian');
Ilaplacian=filter2(model,I1);
figure,imshow(Ilaplacian,[]);

效果：

Figure 13

套用前面自定义模版后的代码如下：

n=3;
model=[0 -1 0;-1 5 -1;0 -1 0];
Iend=I1;
Idouble=double(I1);
for i=1:length(Idouble)-5+n
    for j=1:length(Idouble(2,:))-5+n
        area=Idouble(i:i+n-1,j:j+n-1);
        x=area.*model;
        grad=sum(x(:));
        Iend(i,j)=grad;
    end
end
figure,imshow(Iend);

效果：

Figure 14

与教科书上的效果相同。

1.5 频率域图像增强

频率域增强包括高通滤波器和低通滤波器，主要是使用傅立叶变换和逆变换对图像进行处理。在MATLAB中没有直接的滤波器函数，但是可以结合原理与MATLAB中的数学公式，构造各种滤波器。在本文中，笔者分别构造了理想、Butterworth、指数的高通和低通滤波器，并一一进行了实验。

首先需要提前设定截止频率D0和阶数n。之后就可以套用具体的公式进行计算了。部分代码如下：

n=6;%滤波器的阶数
D0=80;%滤波器的截止频率
[u,v]=meshgrid(-M/2:(M/2-1),-N/2:(N/2-1));%产生离散数据
D=sqrt(u.^2+v.^2);
%各种不同的滤波器
H1=double(D<=D0);%理想低通滤波器
H2=1./(1+(D/D0).^(2*n));%Butterworth低通滤波器
H3=exp(-(D/D0).^n);%指数低通滤波器
H4=double(D>=D0);%理想高通滤波器
H5=1./(1+(D0./D).^(2*n));%Butterworth高通滤波器
H6=exp(-(D0./D).^n);%指数高通滤波器

之后，可以使用各种不同的滤波器对图片进行处理。效果如下：